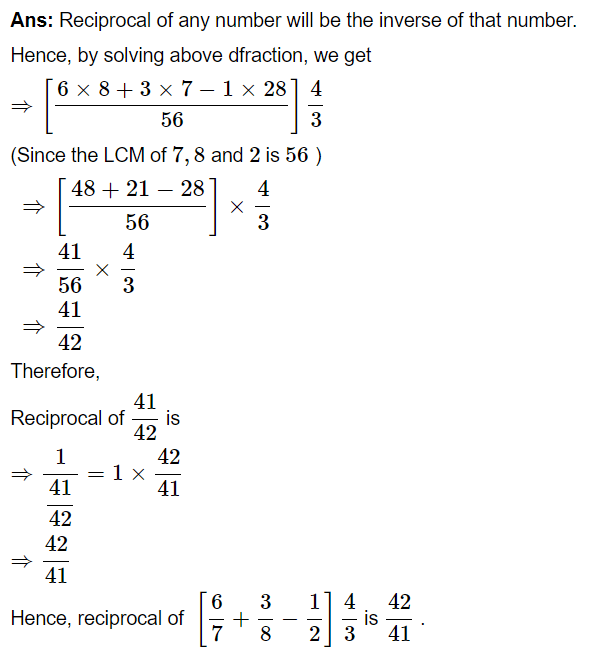Rational Numbers Class 8 Notes Maths Chapter 1
What are Natural Numbers?
Counting numbers starting from 1 are known as natural numbers. i.e., {1, 2, 3, 4....}
What are Whole numbers?
The natural numbers together with 0 are called whole numbers. i.e., {0, 1, 2, 3, 4, 5......}
What are Integers?
The whole numbers and negative of whole numbers together are called Integers. i.e., {...-4, -3, -2, -1, 0, 1, 2, 3, 4...}
What are Rational Numbers?
A number which can be written in the form p/q, where p and q are integers and q ≠ 0 is called a rational number.
For example: − 2/3, 6/7
So here if we multiply or divide the numerator and denominator of a rational number by the same non-zero integer, then we will get another equivalent rational number.
The general form for Equivalent rational number can be written as:
If p/q is any rational number and r/s is its equivalent rational number, then p/q = r/s such that ps = rq where p, q, r, and s are integers such that q and s are non-zero integers.
Example 1:
Let's take the rational number 2/4. Multiplying the numerator and the denominator by 2 we get:
(2 * 2) / (4 * 2) = 4/8
So, 4/8 is an equivalent rational number to 2/4.
Thus, a rational number can be written in several equivalent forms.
Here is an interesting video on "What are rational numbers?"
Properties of Rational Numbers
The list of properties of rational numbers can be given as follows:
- Closure
- Commutativity
- Associativity
- The role of zero (0)
- The role of 1
- Distributivity of multiplication over addition for rational numbers.
Let's discuss each of them in detail:
1. Closure
When we perform any operation on a specific set of numbers (natural number, whole number, integer, etc....) such that the resultant also belongs to the same set then we say it follows closure property over that operation.
(a) Closure Property of Whole Numbers
When we perform any operation on the whole number, such that the resultant also belongs to the same set then we say it follows the closure property of whole numbers over that operation. So,
If any operation of two whole numbers satisfies the above-mentioned property, we say It is closed under that particular operation.
For example:
Let us take examples for various operations,
Let us take two whole numbers 2 and 3
(i) For addition
2 + 3 = 5, which is also a whole number.
So, it is closed under addition.
(ii) For subtraction
2 - 3 = -1, which is not a whole number.
So, it is not closed under subtraction.
(iii) For multiplication
2*3 = 6, which is also a whole number.
So, it is closed under multiplication.
(iv) For division
2 ÷ 3 = 2/3, which is not a whole number.
So, it is not closed under addition.
Let’s summarize this in a table,
 Closure Property for operations on Whole Numbers
Closure Property for operations on Whole Numbers
(b) Closure Property of Integers
When we perform any operation on integer, such that the resultant also belong to the same set then we say it follows closure property of integer over that operation.
So, If any operation of two integers satisfies the above-mentioned property, we say It is closed under that particular operation.
For example:
Let us take examples for various operations,
Let us take two integers -2 and 3
(i) For addition
-2 + 3 = 1, which is also an integer.
So, it is closed under addition.
(ii) For subtraction
-2 - 3 = -5, which is also an integer.
So, it is closed under subtraction.
(iii) For multiplication
-2 * 3 = -6, which is also an integer.
So, it is closed under multiplication.
(iv) For division
-2 ÷ 3 = - 2/3 which is not an integer.
So, it is not closed under division.
Let’s summarize this in a table,
 Closure Property for operations on Integers(c) Closure Property of Rational Numbers
Closure Property for operations on Integers(c) Closure Property of Rational Numbers
When we perform any operation on a rational number, such that the resultant also belong to the same set then we say it follows closure property of rational number over that operation. So,
If any operation of two rational numbers satisfies the above- mentioned property, we say It is closed under that particular operation.
For example:
Let us take examples for various operations,
Let us take two rational numbers 1/15 and - 1/15
(i) For addition
1/15 + (-1/15) = 0, which is also a rational number.
So, it is closed under addition.
(ii) For subtraction
1/15 - (-1/15) = 2/15, which is also a rational number.
So, it is closed under subtraction.
(iii) For multiplication
1/15 × (-1/15) = -1/225, which is also a rational number.
So, it is closed under multiplication.
(iv) For division
1/15 ÷ 0= not defined.
Therefore, any rational number, ‘a’ and ‘0’, then a ÷ 0 is not defined and hence it is not closed. But also, if we exclude ‘0’, then it is closed under division.
Let’s summarize this in a table,
 Closure Property for Operations on Rational Numbers2. Commutativity
Closure Property for Operations on Rational Numbers2. Commutativity
An operation is said to be commutative when if we change the order of operands then the result remains the same, it does not change.
(a) Commutative property of Whole Numbers
If any operation of two whole numbers satisfies the above-mentioned property, we say It is commutative under that particular operation.
For example: Let us take examples for various operation
Let us take two whole numbers 2 and 3
(i) For addition
2 + 3 = 5 and 3+2 = 5
Here, 2 + 3 = 3 + 2
So, it is commutative under addition.
(ii) For subtraction
2 - 3 = -1 and 3 - 2 = 51
Here, 2-3 ≠ 3-2
So, it is not commutative under subtraction.
(iii) For multiplication
2*3 = 6 and 3*2 = 6
Here, 2*3 = 3*2
So, it is commutative under multiplication.
(iv) For division
2÷3 = 2/3 and 3÷2 = 3/2
Here, 2÷3 ≠ 3÷2
So, it is not commutative under division.
Let’s summarize this in a table,
 Commutativity of Whole Numbers
Commutativity of Whole Numbers
(b) Commutative property of Integers
If any operation of two integers satisfies the above-mentioned property, we say It is commutative under that particular operation.
Example:
Let us take examples for various operations,
Let us take two integers -2 and 3
(i) For addition
-2 + 3 = 1 and 3+(-2) = 1
Here, -2+3 = 3+(-2)
So, it is commutative under addition.
(ii) For subtraction
-2 -3 = -5 and 3-(-2) = 5
Here, -2-3 ≠ 3-(-2)
So, it is not commutative under subtraction.
(iii) For multiplication
-2*3 = -6 and 3*(-2) = -6
Here, -2*3 = 3*(-2)
So, it is commutative under multiplication.
(iv) For division
-2 ÷ 3 = -2/3 and 3 ÷ (-2) = 3/(-2)
Here, -2÷3 ≠ 3 ÷ (-2)
So, it is not commutative under division.
Let’s summarize this in a table,
 Commutativity of Integers
Commutativity of Integers
(c) Commutative Property of Rational Numbers
If any operation of two rational numbers satisfies the above-mentioned property, we say It is commutative under that particular operation.
Example:
Let us take examples for various operations,
Let us take two rational numbers 1/5 and 2/5
(i) For addition
1/5 + 2/5 = 3/5 and 2/5 + (1/5) = 3/5
Here, 1/5 + 2/5 = 2/5 + (1/5)
So, it is commutative under addition.
(ii) For subtraction
1/5 - 2/5 = -1/5 and 2/5 - (1/5) = 1/5
Here, 1/5 - 2/5 ≠ 2/5 - (1/5)
So, it is not commutative under subtraction.
(iii) For multiplication
1/5 * 2/5 = 2/25 and 2/5 * (1/5) = 2/25
Here,
1/5 * 2/5 = 2/5 * (1/5)
So, it is commutative under multiplication.
(iv) For division
1/5 * 2/5 = 1/2 and 2/5 ÷ (1/5) = 2
Here, 1/5 ÷ 2/5 ≠ 2/5 ÷ (1/5)
So, it is not commutative under division.
Let’s summarize this in a table, Commutativity of rational numbers
Commutativity of rational numbers
3. Associativity
A set of numbers is said to follow associative property over a particular operation if even after changing the grouping of numbers, we get the same result.
Associative Property of Whole Numbers
If any operation of whole numbers satisfies the above-mentioned property, we say It is associative under that particular operation.
For example:
Let us take examples for various operations,
Let us take three whole numbers 2, 4 and 3.
(i) For addition
(2 + 4) +3 = 6+3 = 9 and 2+(4 + 3) = 2 +7=9
Here, (2+4) +3 = 2+(4+3)
So, it is associative under addition.
(ii) For subtraction
(2 - 4) -3 = -2+(-3) = -5 and 2-(4+3) = 2-1 =1
Here, (2-4)-3 ≠ 2-(4+3)
So, it is not associative under subtraction.
(iii) For multiplication
(2*4)*3 = 8*3 = 24 and 2*(4*3) = 2*12=24
Here, (2*4) *3 = 2*(4*3)
So, it is associative under multiplication
(iv) For division
(2÷4) ÷3 = 0.5÷ (3) = 1/6 and 2÷ (4÷3) = 2÷ 4/3 = 3/2
Here, (2÷4) ÷3 ≠ 2÷ (4÷3)
So, it is not associative under division.
Let’s summarize this in a table, Associative property of whole numbers
Associative property of whole numbers
Associative Property of integers
If any operation of integers satisfies the above-mentioned property, we say It is associative under that particular operation.
For example:
Let us take examples for various operations,
Let us take three whole numbers -2, 4 and 3.
(i) For addition
(-2+4) +3 = 2+3 = 5 and -2+(4+3) = -2+7=5
Here, (-2+4) +3 = -2+(4+3)
So, it is associative under addition.
(ii) For subtraction
(-2-4) -3 = -6+(-3) = -9 and -2-(4-3) = -2-1 =-3
Here, (-2-4)-3 ≠ -2-(4-3)
So, it is not associative under subtraction.
(iii) For multiplication
(-2*4) *3 = -8*3 = -24 and -2*(4*3) = -2*12=-24
Here, (-2*4) *3 = -2*(4*3)
So, it is associative under multiplication
(iv) For division
(-2÷4) ÷3 = -0.5÷ (3) = - 1/6 and -2÷ (4÷3) = -2÷ 4/3 = -3/2
Here, (-2÷4) ÷3 ≠ -2÷ (4÷3)
So, it is not associative under division. Associative property of integers
Associative property of integers
Associative Property of Rational Numbers
If any operation of a rational number satisfies the above-mentioned property, we say It is associative under that particular operation.
For example:
Let us take examples for various operations,
Let us take three whole numbers - 2/5, 2/5, and 1.
(i) For addition
If any operation of a rational number satisfies the above-mentioned property, we say It is associative under that particular operation.
For example:
Let us take examples for various operations,
Let us take three whole numbers - 2/5, 2/5, and 1.
(i) For addition
(-2/5 + 2/5) + 1 = 0 + 1 = 1 and -2/5 + (2/5 + 1) = -2/5 + 7/5 = 1
Here, (-2/5 + 2/5) + 3 = -2/5 + (2/5 + 3)
So, it is associative under addition.
(ii) For subtraction
(-2/5 - 2/5) - 1= -4/5 - 1 = -9/5 and -2/5 (-2/5 - 1) = -2/5 - (-3/5) = 1/5
Here, (-2/5-) - 1 ≠ -2/5 (2/5 - 1)
So, it is not associative under subtraction.
(iii) For multiplication
(-2/5 * 2/5) * 1 = -4/25 * 1 = -4/25 and -2/5*(-2/5*1) = -2/5*2/5 = -4/25
Here, (-2/5 * 2/5) * 1 = -2/5 *(2/5 * 1)
So, it is associative under multiplication
(iv) For division
(-2/5 ÷ 2/5) ÷1 = -1÷ (1) = -1 and -2/5 ÷ (2/5 ÷ 1) = -2/5 ÷ 2/5 = -1
Here, in this case, it is holding equality but let’s take 2 instead of 1.
(-2/5 ÷ 2/5) ÷2 = -1÷ (2) = − 1/2 and -2/5 ÷ (2/5 ÷ 2) = -2/5 ÷ 1/5 = -2
Here, (-2/5 ÷ 2/5) ÷2 ≠ - 2/5 ÷ (2/5 ÷ 2)
So, it is not associative under division.
 Associative property of rational number
Associative property of rational number
Q.1. 
Solution:
Q.2. Find three Rational Number between 3 and 4. Represent them on the Number line.
4. The role of zero (0)
Additive Inverse or Additive Identity of Rational Numbers
When 0 is added to a number, the sum is the same number. Therefore, 0 is called the identity for the addition of rational numbers. It is the additive identity for integers and whole numbers also.
For example:
5 + 0 = 0 + 5 = 5 (Addition of 0 to a whole number)
−5 + 0 = 0 + (−5) = −5 (Addition of 0 to an Integer)
-5/7 + 0 = 0 + -5/7 = -5/7 (Addition of 0 to a rational number)
Q.3. Write the additive inverse of the following:
(a) 3/8
(b) -7/12
(a) We know that additive inverse of a/b is (-a)/b
∴ The additive inverse of 3/8 is (-3)/8
(b) The additive inverse of (-a)/b is a/b
∴ additive inverse of -7/12 is 7/12
Q.5. What number should be added to -11/8 to get 5/9.
Let the number be x.
5. The role of 1
Multiplicative identity of Rational Numbers or Multiplicative Inverse
When 1 is multiplied by any number, the product is again the same number. Therefore 1 is the multiplicative identity for rational numbers, integers, and whole numbers.
For any non-zero rational number a/b there exist a rational number c/d, such that
Q.5. Find the multiplicative inverse of the following:
(a) 5/17
(b) 13
(a) Reciprocal of 5/17 is 17/5
(b) Reciprocal of 13 is 1/13
Q.6. Multiply 6/13 by the reciprocal of -7/6
Reciprocal of -7/6 is -6/7
6. Distributivity of multiplication over addition
To distribute means to divide.
According to the distributive property of multiplication over addition and subtraction, if we multiply the sum or subtraction of two numbers together then the resultant product will be same as the when we take the product of that numbers individually and then do addition or subtraction.
 Q.7. Solve:
Q.7. Solve:
Solution:
Q.8. Solve:
Solution:
|
79 videos|408 docs|31 tests
|
FAQs on Rational Numbers Class 8 Notes Maths Chapter 1
| 1. What are natural numbers and how are they different from whole numbers? |  |
| 2. What are integers and how do they relate to whole numbers and natural numbers? |  |
| 3. What are rational numbers and how can they be identified? |  |
| 4. What is the closure property of rational numbers? |  |
| 5. How does the role of zero (0) and one (1) function in the context of rational numbers? |  |