Ex-18.2 (Part - 2), Surface Area And Volume Of A Cuboid And Cube, Class 9, Math RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q16) A box with lid is made of 2cm thick wood. Its external length, breadth and height are 25cm, 18cm and 15cm respectively. How much cubic cm of a fluid can be placed in it? Also, find the volume of the wood used in it.
Solution:
Given,
The external dimensions of cuboid are as follows
Length (l) = 25 cm
Breadth (b) = 18 cm
Heigth (h) = 15 cm
External volume of the case with cover (cuboid) = l*b*h cm3
= 25*18*15 cm3
= 6750 cm3
Now, the internal dimensions of the cuboid is as follows
Length (l) = 25-(2*2) = 21 cm
Breadth (b) = 18-(2*2) = 14 cm
Height (h) = 15-(2*2) = 11cm
Now, Internal volume of the case with cover (cuboid) = l*b*h cm3
= 21*14*11 cm3
= 3234 cm3
Therefore, Volume of the fluid that can be placed = 3234 cm3
Now, volume of the wood utilized = External volume – Internal volume
= 3516 cm3
Q17) The external dimensions of a closed wooden box are 48cm, 36cm, 30cm. The box is made of 1.5cm thick wood. How many bricks of size 6cm x 3cm x 0.75cm can be put in this box?
Solution:
Given that,
The external dimensions of the wooden box are as follows:
Length (l) = 48cm, Breadth (b) = 36cm, Heigth (h) = 30cm
Now, the internal dimensions of the wooden box are as follows:
Length (l) = 48-(2*1.5) = 45cm
Breadth (b) = 36-(2*1.5) = 33cm
Height (h) = 30-(2*1.5) = 27cm
Internal volume of the wooden box = l*b*h cm3
= 45*33*27 cm3
= 40095 cm3
Volume of the brick = 6*3*0.75 = 13.5 cm3
Therefore,Number of bricks =  = 2970 bricks
= 2970 bricks
Therefore,2970 bricks can be kept inside the wooden box.
Q18) How many cubic centimeters of iron are there in an open box whose external dimensions are 36cm, 25cm and 16.5cm, the iron being 1.5cm thick throughout? If 1 cubic cm of iron weighs 15gms. Find the weight of the empty box in kg.
Solution:
Given,
Outer dimensions of iron:
Length (l) = 36cm
Breadth (b) = 25cm
Heigth (h) = 16.5cm
Inner dimensions of iron:
Length (l) = 36-(2*1.5) = 33cm
Breadth (b) = 25-(2*1.5) = 22cm
Height (h) = 16.5-1.5 = 15cm
Volume of Iron = Outer volume – Inner volume
= (36*25*16.5) – (33*22*15)
= 3960 cm3
Weight of Iron = 3960*15 = 59400 grams = 59.4 kgs
Q19) A cube of 9cm edge is immersed completely in a rectangular vessel containing water. If the dimensions of the base are 15cm and 12cm, find the rise in water level in the vessel.
Solution:
Volume of the cube = S3 = 93 = 729cm3
Area of the base = l*b = 15*12 = 180cm2
Risein water level = 
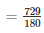
= 4.05cm
Q20) A rectangular container, whose base is a square of side 5cm, stands on a horizontal table, and holds water up to 1cm from the top. When a solid cube is placed in the water it is completely submerged, the water rises to the top and 2 cubic cm of water overflows. Calculate the volume of the cube and also the length of its edge.
Solution:
Let the length of each edge of the cube be ‘x’cm
Then, volume of the cube = Volume of water inside the tank + Volume of water that overflowed
x3 = (5∗5∗1)+2
x3 = 27
x = 3cm
Hence, volume of the cube = 27cm3
And edge of the cube = 3cm
Q21) A field is 200 m long and 150 m broad. There is a plot, 50 m long and 40 m broad, near the field. The plot is dug 7m deep and the earth taken out is spread evenly on the field. By how many meters is the level of the field raised? Give the answer to the second place of decimal.
Solution:
Volume of the earth dug out = 50*40*7 = 14000 m3
Let ‘h’ be the rise in the height of the field
Therefore, volume of the field (cuboidal) = Volume of the earth dug out
⇒ 200∗150∗h = 14000
⇒ h = 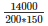 = 0.47m
= 0.47m
Q22) A field is in the form of a rectangular length 18m and width 15m. A pit 7.5m long, 6m broad and 0.8m deep, is dug in a corner of the field and the earth taken out is spread over the remaining area of the field. Find out the extent to which the level of the field has been raised.
Solution:
Let ‘h’metres be the rise in the level of field
Volume of earth taken out from the pit = 7.5*6*0.8 = 36 m3
Area of the field on which the earth taken out is to be spread = 18*15 – 7.5*6 = 225m2
Now, Area of the field * h = Volume of the earth taken out from the pit
⇒ 225∗h = 7.5∗6∗0.8
⇒ h = 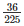 = 0.16m = 16cm
= 0.16m = 16cm
Q23) A rectangular tank is 80m long and 25m broad. Water flows into it through a pipe whose cross-section is 25cm2, at the rate of 16 km per hour. How much the level of the water rises in the tank in 45 minutes?
Solution:
Consider ‘h’ be the rise in water level.
Volume of water in rectangular tank = 8000*2500*h cm2
Cross-sectional area of the pipe = 25 cm2
Water coming out of the pipe forms a cuboid of base area 25 cm2 and length equal to the distance travelled in 45 minutes with the speed 16 km/hour
i.e., length = Length = 16000∗100∗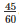 cm
cm
Therefore, The Volume of water coming out pipe in 45 minutes = 25*16000*100* (45/60)
Now, volume of water in the tank = Volume of water coming out of the pipe in 45 minutes
⇒ 8000∗2500∗h = 16000∗100∗4560∗25
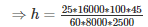 = 1.5cm
= 1.5cm
Q24) Water in a rectangular reservoir having base 80 m by 60 m is 6.5m deep. In what time can the water be pumped by a pipe of which the cross-section is a square of side 20cm if the water runs through the pipe at the rate of 15km/hr.
Solution:
Flow of water = 15km/hr
= 15000 m/hr
Volume of water coming out of the pipe in one hour,
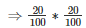 ∗15000 = 600m3
∗15000 = 600m3
Volume of the tank = 80*60*6.5
= 31200 m3
Timetakentoemptythetank = 
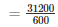 = 52hours
= 52hours
Q25) A village having a population of 4000 requires 150 liters of water per head per day. It has a tank measuring 20m x 15m x 6m. For how many days will the water of this tank last?
Solution:
Given that,
Length of the cuboidal tank (l) = 20m
Breadth of the cuboidal tank (b) = 15m
Height of the cuboidal tank (h) = 6m
Capacity of the tank = l*b*h = 20*15*6
= 1800 m3
= 1800000 litres
Water consumed by the people of village in one day = 4000*150 litres
= 600000 litres
Let water of this tank last for ‘n’ days
Therefore, water consumed by all people of village in n days = capacity of the tank
= n*600000 = 1800000
= n = 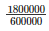 = 3
= 3
Thus, the water will last for 3 days in the tank.
Q26) A child playing with building blocks, which are of the shape of the cubes, has built a structure as shown in Fig. 18.12. If the edge of each cube is 3cm, find the volume of the structure built by the child.
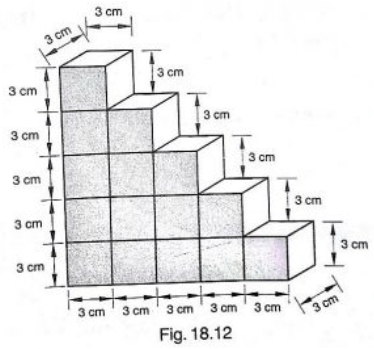
Solution:
Volume of each cube = edge*edge*edge
= 3*3*3
= 27 cm3
Number of cubes in the structure = 15
Therefore, volume of the structure = 27*15
= 405 cm3
Q27) A godown measures 40m x 25m x 10m. Find the maximum number of wooden crates each measuring 1.5m x 1.25m x 0.5m that can be stored in the godown.
Solution:
Given,
Godown length (l1) = 40m
Godown breadth (b1) = 25m
Godown height (h1) = 10m
Volume of the godown = l1* b1* h1 = 40*25*10
= 10000 m3
Wooden crate length (l2) = 1.5m
Wooden crate breadth (b2) = 1.25m
Wooden crate height (h2) = 0.5m
Volume of the wooden crate = l2*b2*h2 = 1.5*1.25*0.5
= 0.9375 m3
The number of wooden crates stored in the godown is taken as ‘n’
Volume of ‘n’ wooden crates = Volume of godown
= 0.9375n = 10000
= n = 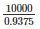 = 10666.66
= 10666.66
Therefore, the number of wooden crates that can be stored in the godown is 10666.66.
Q28) A wall of length 10m was to be built across an open ground. The height of the wall is 4m and thickness of the wall is 24cm. If this wall is to be built up with bricks whose dimensions are 24cm x 12cm x 8cm, how many bricks would be required?
Solution:
Given that,
The wall with all its bricks makes up space occupies by it, we need to find the volume of the wall, which is nothing but cuboid.
Here, length = 10m = 1000cm
Thickness = 24cm
Height = 4m = 400cm
Therefore, volume of the wall = l*b*h
= 1000*24*400 cm3
Now, each brick is a cuboid with length = 24cm
Breadth = 12cm
Height = 8cm
So, volume of each brick = l*b*h = 24*12*8 = 2304 cm3
The number of bricks required is given by,

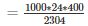 = 4166.6 bricks
= 4166.6 bricks
So, the wall requires 4167 bricks.
FAQs on Ex-18.2 (Part - 2), Surface Area And Volume Of A Cuboid And Cube, Class 9, Math RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. What is the formula for finding the surface area of a cuboid? |  |
| 2. How do you find the volume of a cube? |  |
| 3. Is the surface area of a cube the same as its volume? |  |
| 4. How can I calculate the surface area of a cube if only the volume is given? |  |
| 5. Can the surface area of a cuboid be greater than its volume? |  |
















