NCERT Exemplar Solutions: Construction | Mathematics (Maths) Class 9 PDF Download

Q.1. With the help of a ruler and a compass it is not possible to construct an angle of :
(a) 37.5°
(b) 40°
(c) 22.5°
(d) 67.5°

Correct Answer is Option (b)
Step -1: Find angle by ruler and compass ∠37.5° can be constructed by bisecting 150° twice which can be done by compass. ∠22.5° is the bisector of 90° which can be also constructed using compass. ∠67.5° is the bisector of 135° which can also be drawn using compass.
Step -2: Find 40° why not done by ruler But 40° can not be drawn using ruler and compass.
Hence, option (b) is correct.

Q.2. The construction of a triangle ABC, given that BC = 6 cm, ∠ B = 45° is not possible when difference of AB and AC is equal to:
(a) 6.9 cm
(b) 5.2 cm
(c) 5.0 cm
(d) 4.0 cm

Correct Answer is Option (a)
According to the theorem of inequalities, the sum of any two sides of the triangle is greater than the third side.
Therefore, AC + BC > AB
⇒ BC > AB − AC
Therefore, only the first option that is 6.9 cm does not satisfy the above equation. Rest all the options satisfy the equation.

Q.3. The construction of a triangle ABC, given that BC = 3 cm, ∠C = 60° is possible when difference of  AB and AC is equal to :
(a) 3.2 cm
(b) 3.1 cm
(c) 3 cm
(d) 2.8 cm

Correct Answer is Option (d)
Given, BC = 3cm and ∠ C = 60 ∘
We know that, the construction of a triangle is possible, if sum of two sides is greater than the thirde side of the triangle i.e.,
A B + B C > A C
⇒ B C > A C − A B
⇒ 3 > A C − A B
So, if AC – AB = 2.8 cm, then construction of ΔABC with given conditions is possible.

Q.1. An angle of 52.5° can be constructed. Is the given statement true or false and give reasons for your answer.

We know that
52.5° = 210°/4
It can be written as
52.5° = 1/4 (180° + 30°)
Therefore, the statement is true.

Q.2. An angle of 42.5° can be constructed. Is the given statement true or false and give reasons for your answer.

We know that
42.5° = 1/2 × 85°
85° cannot be constructed using a ruler and a compass
Here 42.5° is not a multiple of 3
So 42.5° cannot be constructed
Therefore, the statement is false.

Q.3. A triangle ABC can be constructed in which AB = 5 cm, ∠A = 45° and BC + AC = 5 cm. Is the given statement true or false and give reasons for your answer.

It is given that
In triangle ABC
AB = 5 cm
∠A = 45°
We know that
A triangle can be constructed if the sum of two sides is greater than the third side
BC + AC = 5 cm which is equal to AB = 5 cm
Therefore, the statement is false.

Q.4. A triangle ABC can be constructed in which BC = 6 cm, ∠C = 30° and AC - AB = 4 cm. Is the given statement true or false and give reasons for your answer.

It is given that
In triangle ABC
BC = 6 cm
∠C = 30°
We know that
A triangle can be constructed if the sum of two sides is greater than the third side
AB + BC > AC
AB + 6 > AC
6 > AC - AB
AC - AB < 6
Therefore, the statement is true.

Q.5. A triangle ABC can be constructed in which ∠ B = 105°, ∠C = 90° and AB + BC + AC = 10 cm. Is the given statement true or false and give reasons for your answer.

It is given that
In triangle ABC
∠B = 105°
∠C = 90°
AB + BC + AC = 10 cm
From the angle sum property of a triangle
∠A + ∠B + ∠C = 180°
Substituting the values
∠B + ∠C = 105° + 90° = 195°
Here
195° > 180° which is not possible
Therefore, the statement is false.

Q.6. A triangle ABC can be constructed in which ∠B = 60°, ∠C = 45° and AB + BC + AC = 12 cm. Is the given statement true or false and give reasons for your answer.

It is given that
In triangle ABC
∠B = 60°
∠C = 45°
AB + BC + AC = 12 cm
From the angle sum property of a triangle
∠A + ∠B + ∠C = 180°
Substituting the values
∠B + ∠C = 60° + 45° = 105°
Here
105° < 180° which is possible
Therefore, the statement is true.

Q.1. Draw an angle of 110° with the help of a protractor and bisect it. Measure each angle.

Construct ∠BXA = 110° using a protractor
Steps of Construction
1. Consider X as centre and taking any radius construct an arc which intersects the rays XA and XB i.e. E and D
2. Considering D and E as centres and radius more than half of DE, construct arcs which intersect each other at F
3. Construct the ray XF
4. XF is the required bisector of angle BXA
5. By measuring each angle
∠BXC = ∠AXC = 1/2 ∠BXA = 110/2
∠BXC = ∠AXC = 55°
Therefore, each angle is 55°.

Q.2. Draw a line segment AB of 4 cm in length. Draw a line perpendicular to AB through A and B, respectively. Are these lines parallel?

Steps of Construction
1. Construct a line segment AB = 4 cm
2. Consider 4 cm as centre and radius more than half of AB construct an arc which intersects AB at the point E
3. Considering E as centre and with same radius construct an arc which intersects the previous arc at the point G
4. Considering G and F as centres construct arcs that intersect each other at the point H
5. Now join AH.
6. AX is the perpendicular to AB at the point A
7. In the same way construct BY perpendicular to AB at the point B.
If two lines are parallel the angle between them will be 0° or 180°
∠XAB = 90° (as XA is perpendicular to AB)
∠YBA = 90° (as YB is perpendicular to AB)
We know that
∠XAB + ∠YBA = 90° + 90° = 180°
As the sum of interior angles on same side of transversal is 180°, the two lines are parallel
So XA and YS are parallel.
Therefore, the lines are parallel.

Q.3. Draw an angle of 80° with the help of a protractor. Then construct angles of (i) 40° (ii)160° and (iii) 120°.

Construct an angle 80° i.e. ∠QOA = 180° using a protractor
Steps of Construction
1. Considering O as radius and any radius construct an arc that intersects OA at the point E and OQ at the point F
2. Considering E and F as centres and radius more than half of EF construct an arc that intersects each other at the point F
3. Now join OP
∠POA = 1/2 x 80° = 40°
4. Considering F as centre and radius equal to EF, construct an arc that intersects previous arcs at the point S
5. Join OS.
∠SOA = 2 x 80° = 160°
6. Considering S and F as centre and radius more than half of SF construct an arc that intersects each other at the point R
7. Join OR
∠ROA = ∠ROQ = 40° + 80° = 120°
Thus, the angles are constructed.

Q.4. Construct a triangle whose sides are 3.6 cm, 3.0 cm and 4.8 cm. Bisect the smallest angle and measure each part.

Steps of Construction
1. Construct a line segment BC of length 4.8 cm
2. From the point B, point A is at a distance of 3.6 cm
3. Considering B as centre construct an arc of radius 3.6 cm
4. From the point C, point A is at a distance of 3.0 cm
5. Considering C as centre construct an arc of radius 3.0 cm that intersects the previous arc at the point A
6. Now join AB and AC
So triangle ABC is the required triangle.
Here angle B is smallest as the smallest side is AC
To construct angle B, use the steps mentioned below.
1. Considering B as centre, construct an arc which intersects AB and BC at the points D and E
2. Considering D and E as centre construct arcs which intersect at the point P
3. By joining BP, we get the angle bisector of ∠B
Here ∠ABC = 39°,
So we get
∠ABD = ∠DBC = 1/2 × 139° = 19.5°
Therefore, the smallest angle ∠B is bisected and each part is 19.5°.

Q.5. Construct a triangle ABC in which BC = 5 cm, ∠B = 60° and AC + AB = 7.5 cm.

Steps of Construction
1. Construct the base BC = 5 cm
2. Make an ∠XBC = 60° at the point B
3. Now cut the line segment BD which is equal to AC + AB = 7.5 cm from BX ray.
4. Join DC.
5. Let us make ∠DCY = ∠BDC
6. Let the ray CY intersect BX at the point A
7. So triangle ABC is the required triangle.
Therefore, triangle ABC is constructed.

Q.6. Construct a square of side 3 cm.

Steps of Construction
1. Construct a line segment AB of length 3 cm
2. Generate 90° at A and B of line segment and marks parallel lines AX and BY at these points.
3. Let us cut AD and SC of 3 cm length from AX and BY
4. Construct an angle of 90° at any one point C or D and join the points by a line segment CD which is 3 cm.
5. So ABCD is the required square of side 3 cm.
Thus, a square of side 3 cm is constructed.

Q.7. Construct a rectangle whose adjacent sides are of lengths 5 cm and 3.5 cm.

Steps of Construction
1. Construct a line segment BC of 5 cm.
2. Generate 90° at B and C of line segment BC and mark the parallel lines BX and CY at these points
3. Cut AB and CD of 3.5 cm length from BX and CY
4. Construct an angle 90° at one point A or D and join both points by AD of length 5 cm
5. ABCD is the required rectangle.
Therefore, ABCD is the rectangle of the required length and breadth.

Q.8. Construct a rhombus whose side is of length 3.4 cm and one of its angles is 45°.

We know that, all sides are equal in a rhombus
Steps of Construction
1. Construct a line segment AB of length 3.4 cm
2. Generate 45° at the ends A and B of line segment AB and mark the parallel lines AX and BY
3. Now cut AD and SC of 3.4 cm length from AX and BY
4. Construct an angle of 45° at one of the point D or C and join both by line segments DC of 3.4 cm length which is parallel to AB
5. So ABCD is the required rhombus with a side of length 3.4 cm and 45° as one of its angles.
Therefore, a rhombus of given length and angle is constructed.

Exercise 11.4

Q.1. A triangle if its perimeter is 10.4 cm and two angles are 45° and 120°. Construct the following and give justification

Consider ABC as a triangle of perimeter 10.4 cm
AB + BC + CA = 10.4 cm and two angles are 45° and 120°
Let us take ∠B = 45° and ∠C = 120°
Steps of Construction
1. Construct a line segment XY of the given length (perimeter of the required triangle) 10.4 cm
2. Construct angle ∠LXY = ∠B = 45° and ∠MYX = ∠C = 120°
3. Now bisect ∠LXY and ∠MYX and let these bisectors intersect at A
4. Construct perpendicular bisectors PQ and RS of AX and AY
5. Let PQ line segment XY at the point B and RS intersect line segment XY at the point C
6. Join AB and AC
7. Triangle ABC is the required triangle
Justification
We know that
B lies on perpendicular bisector PQ of AX
AB + BC + CA = XB + BC + CY = XY
In triangle AXB, AB = XB
So ∠BAX = ∠AXB …. (1)
As ∠ABC is exterior angle of triangle AXB
∠ABC = ∠BAX + ∠AXB
Using equation (1)
∠ABC = ∠AXB + ∠AXB
∠ABC = 2 ∠AXB
∠ABC = ∠LXY (AX is the bisector of ∠LXB)
In triangle AYC, AC = CY
∠CAY = ∠AYC
As ∠ACB is an exterior angle of triangle AYC
∠ACB = ∠CAY + ∠AYC
∠ACB = ∠CAY + ∠CAY
∠ACB = 2∠CAY
∠ACB = ∠MYX (AY is the bisector of ∠MYX)
Therefore, the construction is justified.

Q.2. A triangle PQR given that QR = 3cm, ∠PQR = 45° and QP - PR = 2 cm. Construct the following and give justification

It is given that in triangle PQR,
QR = 3cm
∠ PQR = 45°
QP - PR = 2 cm
C lies on perpendicular bisector RS of AY
Steps of Construction
1. Construct the base QR of 3 cm length
2. Construct ∠XQR = 45° at point Q of the base QR
3. Now cut the line segment QS = QP - PR = 2 cm from the ray QX
4. Join SR and construct the perpendicular bisector of SR say AB
5. Let AB intersect QX at the point P
6. Join PR
7. Triangle PQR is the required triangle
Justification:
∠PQR and base QR are drawn
P lies on perpendicular bisector of SR
PS = PR
QS = PQ - PS
QS = PQ - PR
Therefore, the construction is justified.

Q.3. A right triangle when one side is 3.5 cm and sum of other sides and the hypotenuse is 5.5 cm. Construct the following and give justification

Consider the right triangle as ABC
It is given that
BC = 3.5 cm
∠B = 90°
AB + AC = 5.5 cm
Steps of Construction
1. Construct the base BC = 3.5 cm
2. Construct ∠XBC = 90° at B of base BC
3. Now cut the line segment BD which is equal to AB + AC = 5.5 cm from XB
4. Join DC and construct an ∠DCY which is equal to ∠BDC
5. Let Y intersect BX at the point A
6. So triangle ABC is the required triangle
Justification
∠B and base BC are drawn
In triangle ACD
∠ACD = ∠ADC (from construction)
As the sides opposite to equal angles are equal
AD = AC …. (1)
From equation (1)
AB = BD - AD = BD - AC
BD = AB + BC
Therefore, the construction is justified.

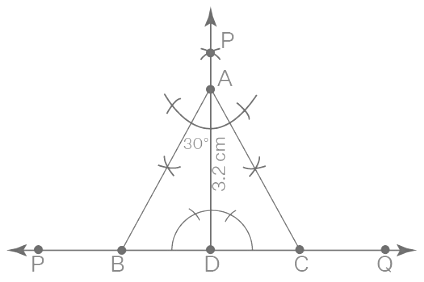
Q.4. An equilateral triangle if its altitude is 3.2 cm. Construct the following and give justification

We know that
In an equilateral triangle all sides and angles are equal
It is given that
Altitude = 3.2 cm
Steps of Construction
1. Construct a line PQ
2. Consider a point D on PQ and construct a ray DE perpendicular to PQ
3. Now cut the line segment AD of 3.2 cm length from DE
4. Construct angles equal to 30° at the point A on both sides of AD i.e. ∠CAD and ∠BAD where B and C lie on PQ
5. Cut the line segment DC from PQ where DC = BD
6. Join AC
7. Triangle ABC is the required triangle

Justification
∠A = ∠BAD + ∠CAD
Substituting the values
∠A = 30° + 30° = 60°
AD is perpendicular to SC
∠ADS = 90°
In triangle ABD using the angle sum property
∠BAD + ∠DBA + ∠BDA = 180°
30° + 90° + ∠DBA = 180°
∠DBA = 60°
In the same way
∠DCA = 60°
So ∠A = ∠B = ∠C = 60°
Therefore, triangle ABC is an equilateral triangle.

Q.5. A rhombus whose diagonals are 4 cm and 6 cm in lengths. Construct the following and give justification

We know that
All sides of a rhombus are equal and the diagonals are perpendicular bisectors of one another
Steps of Construction
1. Construct the diagonal AC of 4 cm length
2. Considering A and C as centres and radius more than half of AC construct arcs on both sides of the line segment AC which intersect each other
3. Now cut both arcs which intersect each other at the point P and Q and join PQ
4. Let PQ intersect line segment AC at O. So PQ is the perpendicular bisector of AC
5. Now cut 3 cm length from OP and OQ, then we get B and D
6. Join AB, BC, CD and DA
7. ABCD is the required rhombus
Justification
D and B lie on the perpendicular bisector of AC
As every point on the perpendicular bisector of line segment is equidistant from end points of line segment
DA = DC and BA = BC …. (1)
∠DOC = 90°
OD = OB = 3 cm
AC is the perpendicular bisector of BD
CD = CB … (2)
AB = BC = CD = DA
From equation (1) and (2)
ABCD is a rhombus.
Therefore, ABCD is a rhombus.