NCERT Solutions for Class 8 Maths - Exponents and Powers - 1 (Exercise 10.1)
Exercise 10.1
Q1: Evaluate(i) 3-2
Sol: (i) To evaluate an expression of the form a-n,where a is a base and n is a positive exponent, we use the rule 
This means we take the reciprocal of the base raised to the positive exponent. So, for 3-2 , this would be: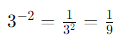
(ii) (-4)-2
Sol: Applying the same rule to (-4)-2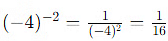
Note that the square of −4 is positive because squaring any real number (whether positive or negative) results in a non-negative number.
(iii) (1/2)-5
Sol: For this expression, we apply the same principle: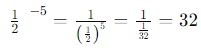
In this case, 1/2 raised to the power of 5 gives 1/32 and taking the reciprocal of that gives us 32.
To summarize: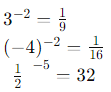
Q2: Simplify and express the result in power notation with positive exponent.
(i) (– 4)5 ÷ (– 4)8
Sol: When we divide powers with the same base, we subtract the exponents: 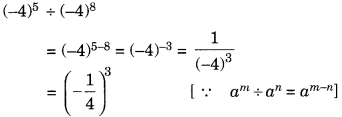
(ii) (1/23)2
Sol: When we raise a power to another power, we multiply the exponents: 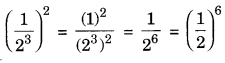
(iii) 
Sol: When multiplying powers with the same exponent but different bases, we can combine them under the same exponent: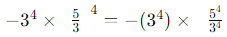
=−(1)×54 =−54
This result cannot be expressed with a positive exponent due to the negative sign in front of 54 .
(iv) 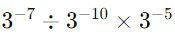
Sol: First, divide the powers with the same base: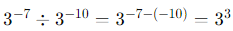
Then, multiply by 3-5: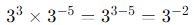
To express with a positive exponent: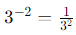
(v) 2–3 × (–7)–3
Sol: Both bases are raised to negative exponents, so we find their reciprocals and multiply: 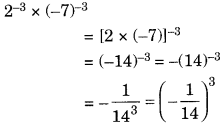
Q3: Find the value of
(i) 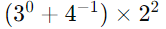
First, evaluate each term inside the parentheses:
30 =1 (Any number raised to the power of 0 is 1.)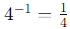 (Negative exponents indicate the reciprocal of the base raised to the positive exponent.)
(Negative exponents indicate the reciprocal of the base raised to the positive exponent.)
So, the expression becomes: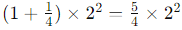
22 =4, thus: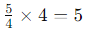
(ii)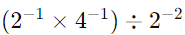
Simplify inside the parentheses first: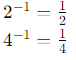
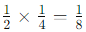
For the division: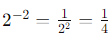
So, the expression simplifies to: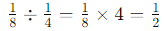
(iii) 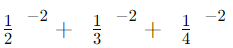
Evaluate each term: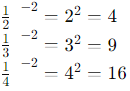
Summing them up:
4 + 9 + 16 = 29
(iv) 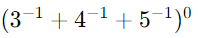
Any expression raised to the power of 0 is 1, regardless of what the expression inside the parentheses evaluates to. So, without needing to simplify the expression inside, the result is: 1
(v) 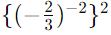
First, evaluate the expression inside the curly braces: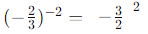
When raising a fraction to a negative exponent, you take the reciprocal of the base and then square it: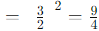
Then, raising this result to the power of 2: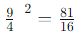
Q4: Evaluate.
(i) 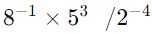
Sol: First, simplify the numerator and the denominator separately:
So, the expression becomes: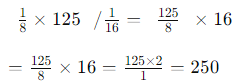
(ii) 
Sol: Simplify each term: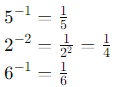
So, the expression becomes:
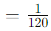
To summarize: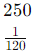
Q5: Find the value of m for which

Sol: To find the value of m for which 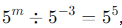 we can use the properties of exponents to simplify the equation. When dividing numbers with the same base, you subtract the exponents:
we can use the properties of exponents to simplify the equation. When dividing numbers with the same base, you subtract the exponents:

So, we have:
5m+3 = 55
For this equation to be true, the exponents on both sides must be equal (since the bases are the same and non-zero). Therefore, we set the exponents equal to each other:
m + 3 = 5
To solve for m, we subtract 3 from both sides:
m=5−3
m=2
So, the value of m for which the original equation holds true is 2.
Q6: Evaluate.


Sol: (i)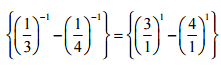

= (3-4) = -1
(ii)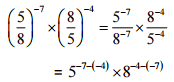


Q7: Simplify.


Sol: (i)



(ii)




Exercise 10.2
Q1. Express the following numbers in standard form.
(i) 0.0000000000085
Sol: This number is 8.5 followed by 11 decimal places to the left, so in standard form, it is:
8.5 × 1 0 − 12
(ii) 0.00000000000942
Sol: This number is 9.42 followed by 11 decimal places to the left, so in standard form, it is:
9.42 × 1 0 − 12
(iii) 6020000000000000
Sol: This number is 6.02 followed by 15 places to the right, so in standard form, it is: 6.02 × 10 15
(iv) 0.00000000837
Sol: This number is 8.37 followed by 9 decimal places to the left, so in standard form, it is: 8.37 × 10 − 9
(v) 31860000000
Sol: This number is 3.186 followed by 10 places to the right, so in standard form, it is:
3.186 × 1 010
Q2: Express the following numbers in usual form.
(i) 3.02×10−6
Sol: Shift the decimal point 6 places to the left:
0.00000302
(ii) 4.5 * 104
Sol: Shift the decimal point 4 places to the right:
45,000
(iii) 3 * 10–8
Sol: Shift the decimal point 8 places to the left:
0.00000003
(iv) 1.0001 * 109
Sol: Shift the decimal point 9 places to the right:
1,000,100,000
(v) 5.8 * 1012
Sol: Shift the decimal point 12 places to the right:
5,800,000,000,000
(vi) 3.61492 * 106
Sol: Shift the decimal point 6 places to the right:
3,614,920
Q3. Express the number appearing in the following statements in standard form.
(i) 1 micron is equal to 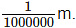
Sol: This can be written as:
1×10−6m
(ii) Charge of an electron is 0.000,000,000,000,000,000,16 coulomb.
Sol: This is:
1.6×10 −19 coulomb
(iii) Size of a bacteria is 0.0000005 m.
Sol: This can be expressed as:
5×10 −7 m
(iv) Size of a plant cell is 0.00001275 m.
Sol: This is:1.275×10 −5 m
(v) Thickness of a thick paper is 0.07 mm.
Sol: To express this in meters and in standard form (considering 1 mm = 0.001 m 1 mm=0.001 m):
0.07 mm=0.07×0.001 m=7×10 −2 m
Q4: In a stack there are 5 books each of thickness 20 mm and 5 paper sheets each of thickness 0.016 mm. What is the total thickness of the stack?
Sol: To find the total thickness of the stack, we need to sum the thicknesses of all the books and paper sheets.
Books Each book has a thickness of 20 mm. For 5 books, the total thickness is:
5 × 20 mm = 100 mm
Paper Sheets
Each paper sheet has a thickness of 0.016 mm. For 5 paper sheets, the total thickness is:
5×0.016mm=0.08mm
Total Thickness
Adding the thicknesses of the books and paper sheets together gives the total thickness of the stack:
100mm+0.08mm=100.08mm
Therefore, the total thickness of the stack is 100.08 mm.
|
79 videos|408 docs|31 tests
|
FAQs on NCERT Solutions for Class 8 Maths - Exponents and Powers - 1 (Exercise 10.1)
| 1. What is an exponent? |  |
| 2. How do you simplify expressions with exponents? |  |
| 3. What is the difference between a base and an exponent? |  |
| 4. How do you solve problems involving negative exponents? |  |
| 5. Can exponents be fractions or decimals? |  |

|
Explore Courses for Class 8 exam
|

|


















