Class 9 Maths Chapter 6 Question Answers - Lines and Angles
Q1. On Monday Prashant’s school bus was late due to a traffic jam and his maths class was missed. He was very upset as his teacher had introduced a new topic on geometry. Rahul promised to help him after school. Rahul went to Prashant’s house and explained the topic. He also gave him the following test also: Which of the following statements are true?
(a) Two adjacent angles are said to form a linear pair of angles if their uncommon arms are two opposite rays.
(b) The sum of all the angles around a point is equal to 180°.
(c) The measure of an angle is twice the measure of its supplementary angle. Its measure is 60°.
(d) The angle between the bisectors of a linear pair of angles is a right angle.
(e) Three or more lines are said to be concurrent if there is a point that lies on all of them.
(i) Write the appropriate answers to the above questions.
(ii) Which mathematical concept is used in the above problem?
(iii) By explaining the topic to Prashant, which value is depicted by Rahul?
Solution. (i) The appropriate answers are:
(a) True
(b) False
(c) False
(d) True
(e) True
(ii) Lines and Angles (Geometry).
(iii) Helping a friend in need.
Q2. Three friends plan to help flood victims. They move away from a point in three different directions such that the direction of each is equally inclined to those of the other two:
(i) Find the angles their directions make with another.
(ii) Which mathematical concept is used in the above problem?
(iii) By helping the flood victims, which value is depicted by the teachers and students?
Solution. (i) Let ‘O’ be the point from where the three friends move to the points A, B and C, such that OA makes equal angles with OB and OC such that
∠AOB = ∠AOC ..... (i)
Also, OB makes equal angles with OA and OC
Such that
∠AOB = ∠BOC ..... (ii)
From (i) and (ii), we get
∠AOB = ∠BOC = ∠AOC ..... (iii)
Since the sum of all angles around a point = 360°
⇒ ∠AOB + ∠BOC + ∠AOC = 360°
⇒ ∠AOB + ∠AOB + ∠AOB = 360° [from iii]
⇒ 3 ∠AOB = 360°
⇒ ∠AOB = (360°/3)= 120°
∴ From (iii), we have: ∠BOC = 120° and ∠AOC = 120°
(ii) Lines and Angles (Geometry)
(iii) Helping attitude towards disastrous victims.
Q3. Maths teacher draws a straight line AB shown on the blackboard as per the following figure.

- Now he told Raju to draw another line CD as in the figure
- The teacher told Ajay to mark ∠AOD as 2z
- Suraj was told to mark ∠AOC as 4y
- Clive Made and angle ∠COE = 60°
- Peter marked ∠BOE and ∠BOD as y and x respectively
Now answer the following questions:
- What is the value of x?
- What is the value of y?
- What is the value of z?
- What should be the value of x + 2z?
- What is the relation between y and z?
Solution:
- (b) 96°
- (d) 24°
- (c) 42°
- (c) 180°
- (a) 2y + z = 90°
Q4. Reeta and Rohan were playing a game on parallel lines and the angles formed with the transverse line(ie alternate angles, corresponding angle and interior angles). First Reeta drew a straight line AB, then Rohan drew another straight line CD||AB. Further, a transverse line PQ was drawn which intersects lines AB and CD at points X and Y respectively
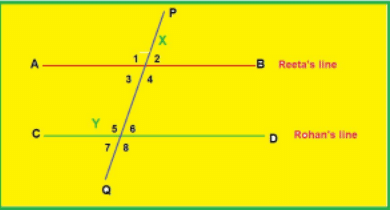
Now they did toss with a coin and Rohan won the toss. Following were the rules of the game:
i. Toss winner will ask a question and others will answer.
ii. If the answer is correct then person answering will ask question else questioner will ask next question.
iii. Who wins the last question he/she will be the winner.
iv. Total of 5 questions will be asked.
1. Which is the alternate angle to ∠6?
2. Which is the corresponding angle to ∠1?
3. If 4 = 120° then what is measure of ∠6?
4. What is the sum of ∠3 and ∠5?
Solution:
1. ∠3
2. ∠5
3. In the diagram, ∠4 and ∠6 are corresponding angles.
So, ∠4 = ∠6
Therefore, if ∠4 is 120∘ then:
∠6 is also 120∘
4. These angles are also known as consecutive interior angles.
The sum of the measures of consecutive interior angles is always 180∘ when the lines are parallel.
Therefore, the sum of angle 3 and angle 5 is:
∠3+ ∠ 5=180∘
|
40 videos|471 docs|57 tests
|
FAQs on Class 9 Maths Chapter 6 Question Answers - Lines and Angles
| 1. What are the different types of angles in geometry? |  |
| 2. How do you determine if two lines are parallel? |  |
| 3. What is the sum of interior angles of a triangle? |  |
| 4. How do you calculate the measure of an exterior angle of a triangle? |  |
| 5. What is the relationship between vertical angles? |  |

















