NCERT Exemplar Solutions: Mensuration | Mathematics for Class 6 PDF Download
Exercise Page: 93
In questions 1 to 6, out of the four options only one is correct. Write the correct answer.
Q1: Following figures are formed by joining six unit squares. Which figure has the smallest perimeter in Fig. 6.4?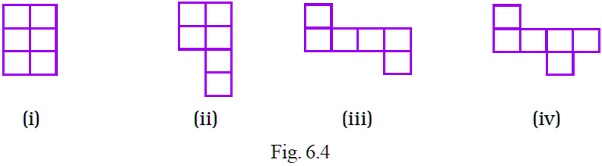
 View Answer
View Answer 
Figure (i) has the smallest perimeter.
Perimeter of a closed figure is the distance covered in one round along the boundary of the figure.
We know that, perimeter of figure = numbers of sides × length of each sides
Consider the given figures,
(i) figure (i) has 10 units and each side have length 1 cm
So, perimeter = 10 × 1
= 10 cm
(ii) figure (ii) has 12 units and each side have length 1 cm
So, perimeter = 12 × 1
= 12 cm
(iii) figure (iii) has 14 sides and each side have length 1 cm
So, perimeter = 14 × 1
= 14 cm
(iv) figure (iv) has 14 sides and each side have length 1 cm
So, perimeter = 14 × 1
= 14 cm
By comparing all the perimeters of given figures, figure (i) has smallest perimeter.
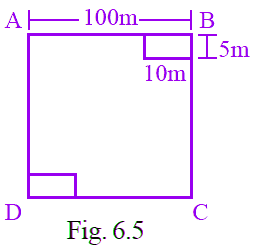
Q2: A square shaped park ABCD of side 100m has two equal rectangular flower beds each of size 10m × 5m (Fig. 6.5). Length of the boundary of the remaining park is
 (a) 360m
(a) 360m
(b) 400m
(c) 340m
(d) 460m
 View Answer
View Answer 
Ans: (b)
We know that, Length of the boundary = Perimeter of boundary
Given, two rectangular flower beds each of size 10m × 5m
So, perimeter of remaining park = 90 + 5 + 10 + 95 + 90 + 5 + 10 + 95
= 400 m
Q3: The side of a square is 10cm. How many times will the new perimeter become if the side of the square is doubled?
(a) 2 times
(b) 4 times
(c) 6 times
(d) 8 times
 View Answer
View Answer 
Ans: (a)
As we know that, perimeter of square = side × 4
= 10 × 4
= 40 cm
Given, side of square = 10 cm
The side of the square is doubled = 10 + 10
= 20 cm
Therefore, the new perimeter becomes 2 times the side of the square is doubled.
Q4: Length and breadth of a rectangular sheet of paper are 20cm and 10cm, respectively. A rectangular piece is cut from the sheet as shown in Fig. 6.6. Which of the following statements is correct for the remaining sheet?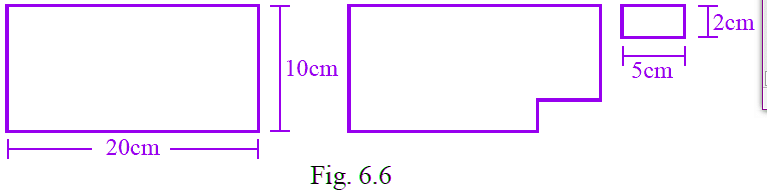
(a) Perimeter remains same but area changes.
(b) Area remains the same but perimeter changes.
(c) Both area and perimeter are changing.
(d) Both area and perimeter remain the same.
 View Answer
View Answer 
Ans: (a)
(A) Perimeter remains same but area changes.
We know that, area of big rectangle = length × breadth
= 10 × 20
= 200 cm2
Area of small rectangle = 5 × 2
= 10 cm2
Perimeter of rectangle = 2(length + breadth)
= 2(20 + 10)
= 2 × 30
= 60 cm
Then, perimeter of new figure = 20 + 8 + 5 + 2 + 15 + 10
= 60
Area of new figure = Area of big rectangle – Area of new figure
= 200 – 10
= 190 cm2
By comparing all the results, Perimeter remains same but area changes.
Q5: Two regular Hexagons of perimeter 30cm each are joined as shown in Fig. 6.7. The perimeter of the new figure is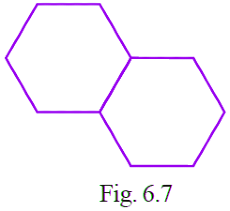 (a) 65cm
(a) 65cm
(b) 60cm
(c) 55cm
(d) 50cm
 View Answer
View Answer 
Ans: (d)
From the question it is given that, perimeter of each hexagon = 30 cm
We know hat, hexagon has 6 sides.
So, length of each side of hexagon = 30/6
= 5 cm
Now, consider two hexagons are joined together.
Then, perimeter of new figure = number of sides × length of each side
= 10 × 5
= 50 cm
Q6: In Fig. 6.8 which of the following is a regular polygon? All have equal sides except (i)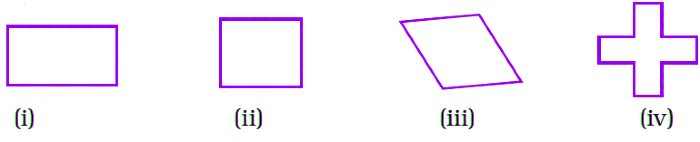
(a) (i)
(b) (ii)
(c) (iii)
(d) (iv)
 View Answer
View Answer 
Ans: (b)
A closed figure in which all sides and angles are equal is called a regular polygon.
Q7: Match the shapes (each sides measures 2cm) in column I with the corresponding perimeters in column II: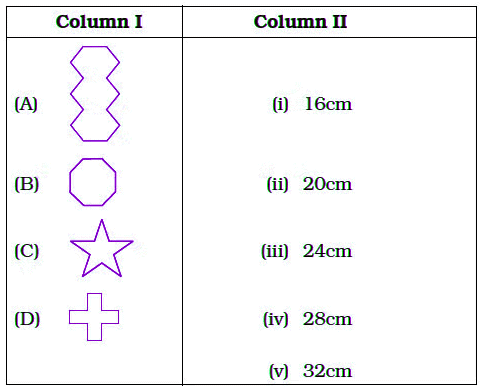
 View Answer
View Answer 
Given, each side measures 2cm.
Figure (A) has 14 sides.
Perimeter of figure = number of sides × length of each side
= 14 × 2
= 28 cm
Figure (B) has 8 sides.
Perimeter of figure = number of side × length of each side
= 8 × 2
= 16 cm
Figure (C) has 10 sides.
Perimeter of figure = number of sides × length of each side
= 10 × 2
= 20 cm
Figure (D) has 12 sides.
Perimeter of figure = number of sides × length of each side
= 12 × 2
= 24 cm
Q8: Match the following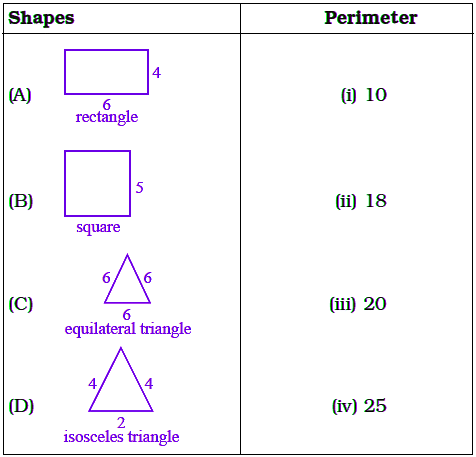
 View Answer
View Answer 
(A) Perimeter of a rectangle = 2 × (length + breadth)
= 2 × (6 + 4)
= 2 × 10
= 20
(B) Perimeter of a square = 4 × length of its side
= 4 × 5
= 20
(C) Perimeter of an equilateral triangle = 3 × length of a side
= 3 × 6
= 18
(D) perimeter of isosceles triangle = sum of length of all sides
= 4 + 4 + 2
= 10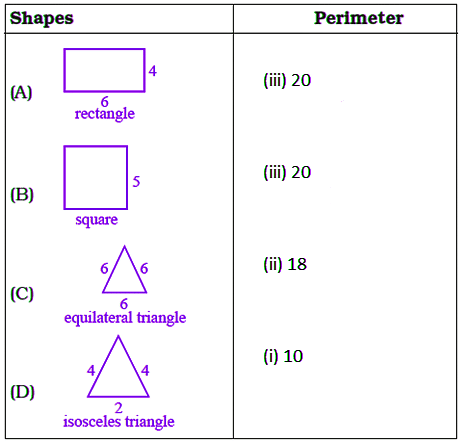
In questions 9 to 13, fill in the blanks to make the statements true.
Q9: Perimeter of the shaded portion in Fig. 6.9 is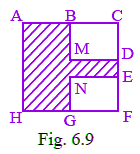
AB + _ + _ + _ + _ + _ + _ + HA
 View Answer
View Answer 
We know that perimeter of a figure = sum of length of all sides
= AB + BM + MD + DE + EN + NG + GH + HA
Q10: The amount of region enclosed by a plane closed figure is called its _________.
 View Answer
View Answer 
The amount of region enclosed by a plane closed figure is called its area.
Q11: Area of a rectangle with length 5cm and breadth 3cm is _________.
 View Answer
View Answer 
Area of a rectangle with length 5cm and breadth 3cm is 15 cm.
Area of rectangle = length × breadth
= 5 cm × 3 cm
= 15 cm
Q12. A rectangle and a square have the same perimeter (Fig. 6.10).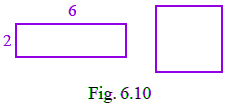
(a) The area of the rectangle is _________.
 View Answer
View Answer 
The area of the rectangle is 12 sq. units.
From figure, length of rectangle is 6 and breadth is 2.
Then, area of rectangle = length × breadth
= 6 × 2
= 12 sq. units
Perimeter of rectangle = 2 × (length + breadth)
= 2 × (6 + 2)
= 2 × 8
= 16 units
(b) The area of the square is _________.
 View Answer
View Answer 
The area of the square is 16 sq. Units.
From the question it is given that, rectangle and a square have the same perimeter.
So, length of each side of a square = 16/4
= 4 units.
Area of square = side × side
= 4 × 4
= 16 sq. Units
Q13: (a) 1 m = _________ cm.
 View Answer
View Answer 
1 m = 100 cm.
(b) 1 sqcm = _________ cm × 1cm.
 View Answer
View Answer 
1 sqcm = 1 cm × 1cm.
(c) 1 sqm = 1 m × _________ m = 100 cm × _________ cm.
 View Answer
View Answer 
1 sqm = 1 m × 1 m
= 100 cm × 100 cm.
(d) 1 sqm = _________ sqcm.
 View Answer
View Answer 
1 sqm = 10000 sqcm.
We know that, 1 m = 100 cm
Then, 1 sqm = 100 × 100
= 10000 sqcm
In questions 14 to 20, state which of the statements are true and which are false.
Q14: If length of a rectangle is halved and breadth is doubled then the area of the rectangle obtained remains same.
 View Answer
View Answer 
True.
We know that, area of rectangle = length × breadth
As per the condition given in the question, length of a rectangle is halved = l/2
Breadth is doubled = 2b
Then, new area = l/2 × 2b
= l × b.
Therefore, if length of a rectangle is halved and breadth is doubled then the area of the rectangle obtained remains same.
Q15: Area of a square is doubled if the side of the square is doubled.
 View Answer
View Answer 
False
We know that, area of square = side × side
As per the condition given in the question, side of the square is doubled = 2 × side
Then, new area = 2side × 2side
= 4 side2
Therefore, if the side of the square is doubled then the area of the square obtained is 4 times the old area.
Q16: Perimeter of a regular octagon of side 6cm is 36cm.
 View Answer
View Answer 
False.
Perimeter of regular octagon = number of sides × length of reach sides
= 8 × 6
= 48 cm
Q17: A farmer who wants to fence his field, must find the perimeter of the field.
 View Answer
View Answer 
True.
Q18: An engineer who plans to build a compound wall on all sides of a house must find the area of the compound.
 View Answer
View Answer 
False.
An engineer who plans to build a compound wall on all sides of a house must find the perimeter of the compound.
Q19: To find the cost of painting a wall we need to find the perimeter of the wall.
 View Answer
View Answer 
False.
To find the cost of painting a wall we need to find the area of the wall.
Q20: To find the cost of a frame of a picture, we need to find the perimeter of the picture.
 View Answer
View Answer 
True.
Q21: Four regular hexagons are drawn so as to form the design as shown in Fig. 6.11. If the perimeter of the design is 28cm, find the length of each side of the hexagon.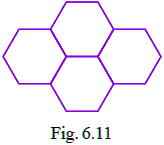
 View Answer
View Answer 
From the question it is given that, the perimeter of the design is 28cm.
Given design has 14 sides, so length of each side = 28/14 = 2 cm
In the given figure, 4 regular hexagons are joined.
Therefore, the length of each side of the hexagon = 2 cm
Q22: Perimeter of an isosceles triangle is 50cm. If one of the two equal sides is 18cm, find the third side.
 View Answer
View Answer 
From the question it is given that, one of the two equal sides is 18cm.
And Perimeter of an isosceles triangle is 50cm
We know that, perimeter of isosceles triangle = sum of all sides
Let us assume the third side be x.
Then,
50 = 18 + 18 + x
50 = 36 + x
X = 50 – 36
X = 14 cm
Therefore, the length of third side of an isosceles triangle is 14 cm.
Q23: Length of a rectangle is three times its breadth. Perimeter of the rectangle is 40cm. Find its length and width.
 View Answer
View Answer 
From the question it is given that,
Perimeter of rectangle = 40 cm
Length of a rectangle is three times its breadth = 3b
We know that, perimeter of rectangle = 2 × (length + breadth)
40 = 2 × (3b + b)
40 = 2 × 4b
40 = 8b
40/8 = b
b = 5 cm
Therefore, width of rectangle = 5 cm
Length of rectangle = 3b
= 3 × 5
= 15 cm
Q24: There is a rectangular lawn 10m long and 4m wide in front of Meena’s house (Fig. 6.12). It is fenced along the two smaller sides and one longer side leaving a gap of 1m for the entrance. Find the length of fencing.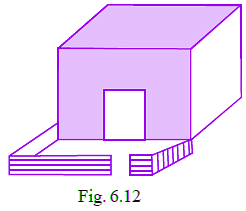
 View Answer
View Answer 
From the question it is given that,
Length of rectangular lawn = 10m
Width of rectangular lawn = 4m
Then,
Perimeter of fencing = length of fencing
Perimeter of fencing = two smaller sides + one longer side – gap in the longer side
= 4 + 4 + 10 – 1
= 18 – 1
= 17 m
Therefore, length of fencing is 17 m.
Q25: The region given in Fig. 6.13 is measured by taking  as a unit. What is the area of the region?
as a unit. What is the area of the region?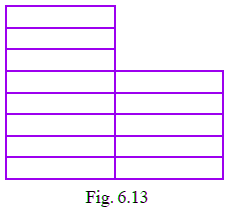
 View Answer
View Answer 
From the question it is given that, a region measured by taking rectangle is as one unit.
Given figure contain 13 rectangles.
Therefore, area of the region = 13 × 1
= 13 sq. Units
Q26: Tahir measured the distance around a square field as 200 rods (lathi). Later he found that the length of this rod was 140cm. Find the side of this field in metres.
 View Answer
View Answer 
From the question it is given that,
Tahir measured the distance around a square field as 200 rods
Length of the rod = 140 cm
So, total distance of square field = 200 × 140
= 28000 cm
Then, length of one side of square field = 28000/4
= 7000 cm
We know that, 1 m = 100 cm
Therefore, side of field = 7000/100
= 70 m
Q27: The length of a rectangular field is twice its breadth. Jamal jogged around it four times and covered a distance of 6km. What is the length of the field?
 View Answer
View Answer 
From the question it is given that,
The length of a rectangular field is twice its breadth = 2b
Perimeter of rectangular field = 6km/4
= 1.5 km
We know that, perimeter of rectangle = 2 × (length + breadth)
1.5 = 2 × (2b + b)
1.5 = 2 × 3b
1.5 = 6b
b = 1.5/6
b = 0.25 km
length of rectangle field = 2 × 0.25 = 0.5km
= 0.5 × 1000
= 500 m
Q28: Three squares are joined together as shown in Fig. 6.14. Their sides are 4cm, 10cm and 3cm. Find the perimeter of the figure.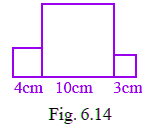
 View Answer
View Answer 
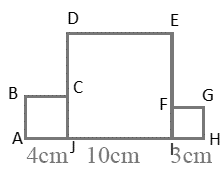
We know that, perimeter of figure = sum of all sides
= AB + BC + CD + DE + EF + FG + GH + HI + JI +JA
= 4 + 4 + (10 – 4) + 10 + (10 – 3) + 3 + 3 + 3 + 10 + 4
= 4 + 4 + 6 + 10 + 7 + 3 + 3 + 3 + 10 + 4
= 54 cm
Q29: In Fig. 6.15 all triangles are equilateral and AB = 8 units. Other triangles have been formed by taking the mid points of the sides. What is the perimeter of the figure?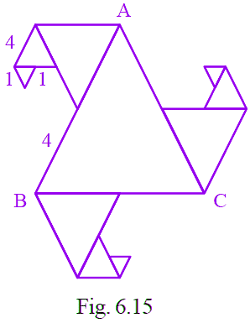
 View Answer
View Answer 
45 units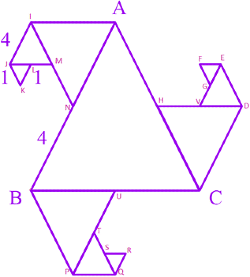
Perimeter of given figure = sum of length of each side
= BN + NM + ML + LK + KJ + JI + IA + AH + HV + VG + GF + FE + ED + DC + UC + UT + TS + SR + RQ + PQ + BP
= 4 + 2 + 1 + 1 + 1 + 2 + 4 + 4 + 2 + 1 + 1 + 1 + 2 + 4 + 4 + 2 + 1 + 1 + 1 + 2 + 4
= 45 units
Q30: Length of a rectangular field is 250 m and width is 150 m. Anuradha runs around this field 3 times. How far did she run? How many times she should run around the field to cover a distance of 4km?
 View Answer
View Answer 
From the question it is given that,
Length of a rectangular field is 250 m
Width of rectangular field = 150 m
Perimeter of rectangle = 2 × (length + breadth)
= 2 × (250 + 150)
= 2 × 400
= 800 m
Given that, Anuradha runs around this field 3 times = 3 × 800
= 2400 m
We know that, 1 km = 1000 m
So, 2400/1000
= 2.4 km i.e. 2 km 400 m
Number of times Anuradha should run around the field to cover a distance of 4 km = 4000/800
= 5 times
Therefore, 5 times Anuradha should run around the field to cover a distance of 4 km.
Q31: Bajinder runs ten times around a square track and covers 4 km. Find the length of the track.
 View Answer
View Answer 
Let a be the side of the square track.
Perimeter of the square track = 4a
Bajinder runs ten times around the square track and covers 4 km, i.e.,
10 × 4a = 4 km
40a = 4 × 1000 m [∵ 1 km = 1000 m]
a = (4 × 1000) / 40 m = 100 m
Length of the track = 4a = 4 × 100 m = 400 m.
Q32: The lawn in front of Molly’s house is 12 m × 8 m, whereas the lawn in front of Dolly’s house is 15 m × 5 m. A bamboo fencing is built around both the lawns. How much fencing is required for both?
 View Answer
View Answer 
Given, size of lawn in front of Molly’s house = 12 m × 8 m
Size of lawn in front of Dolly’s house = 15 m × 5 m
Now, fencing required for both = 2(12 + 8) + 2(15 + 5)
= 40 + 40 = 80m.
Q33: The perimeter of a regular pentagon is 1540 cm. How long is each side?
 View Answer
View Answer 
Given, perimeter of pentagon = 1540 cm
Sides in pentagon = 5
5 × side = 1540
Now, length of each side = 1540 / 5 = 308 cm.
Q34: The perimeter of a triangle is 28 cm. One of its sides is 8cm. Write all the sides of the possible isosceles triangles with these measurements.
 View Answer
View Answer 
Given, Perimeter of a triangle = 28 cm
One of its sides = 8 cm
Let two equal sides of the isosceles triangle be a.
Now we have, a + a + 8 = 28
2a + 8 = 28
2a = 20
a = 10 cm
All sides of the isosceles triangle are 8 cm, 10 cm, and 10 cm.
Q35: The length of an aluminium strip is 40 cm. If the lengths in cm are measured in natural numbers, write the measurement of all the possible rectangular frames which can be made out of it.
 View Answer
View Answer 
Given length of aluminium strip = 40 cm
This implies, we have the perimeter of the rectangular frame = 40 cm
Now 2(l + b) = 40
l + b = 20
From this equation, we can suggest values of l and b as 19×1 cm, 18×2 cm, 16×4 cm, and many more.
Q36: Base of a tent is a regular hexagon of perimeter 60cm. What is the length of each side of the base?
 View Answer
View Answer 
Given perimeter of hexagon = 60 cm
No. of sides in hexagon = 6
Now, length of each side of hexagon = 60 / 6 = 10 cm.
Q37: In an exhibition hall, there are 24 display boards each of length 1m 50 cm and breadth 1 m. There is a 100 m long aluminium strip, which is used to frame these boards. How many boards will be framed using this strip? Find also the length of the aluminium strip required for the remaining boards.
 View Answer
View Answer 
Given, Total number of display boards = 24
Length of strip = 100 m
Length of each display board = 1.5 m
Breadth of one display board = 1 m
Perimeter of one display board = 2(l + b) = 2 (1.5 + 1) = 5 m
Now, number of boards which will be framed = 100 / 5 = 20
Thus, number of boards remained unframed = 24 – 20 = 4
Length of strip required for remaining boards = 4 × 5 = 20 m.
Q38: In the above question, how many square metres of cloth is required to cover all the display boards? What will be the length in metres of the cloth used, if its breadth is 120 cm?
 View Answer
View Answer 
As given, Length of display board = 1m 50 cm = 1.5 m
Breadth of display board = 1m
Area of 24 display boards = 24(l × b) = 24(1.5 × 1) = 24 × 1.5 = 36 sqm
Therefore, 36 sqm of cloth is required to cover all the display boards.
Now, breadth of cloth = 120 cm = 1.2m
Length of cloth = 36 / 1.2 = 30 m.
Q39: What is the length of the outer boundary of the park shown in Fig. 6.16? What will be the total cost of fencing it at the rate of Rs 20 per metre? There is a rectangular flower bed in the center of the park. Find the cost of manuring the flower bed at the rate of Rs 50 per square metre.
 View Answer
View Answer 
The length of the outer boundary of the park = (200 + 300 + 80 + 300 + 200 + 260) m = 1340 m
Cost of fencing the park at the rate of Rs. 20 per metre = Rs. (20 × 1340) = Rs 26800
Area of the flower bed = (100 × 80) = 8000 sqm
Cost of manuring the flower bed at the rate of Rs. 50 per square metre = Rs. (50 × 8000) = Rs. 400000.
Q40: Total cost of fencing the park shown in Fig. 6.17 is Rs. 55000. Find the cost of fencing per metre.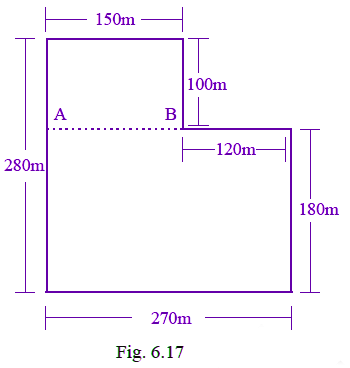
 View Answer
View Answer 
Given, perimeter of the given figure = 150 + 100 + 120 + 180 + 270 + 280 = 1100m
Total cost of fencing = Rs. 55000
Cost of fencing per metre = 55000 / 1100 = Rs. 50.
Q41: In Fig. 6.18 each square is of unit length.
(a) What is the perimeter of the rectangle ABCD?
(b) What is the area of the rectangle ABCD?
(c) Divide this rectangle into ten parts of equal area by shading squares. (Two parts of equal area are shown here)
(d) Find the perimeter of each part which you have divided. Are they all equal?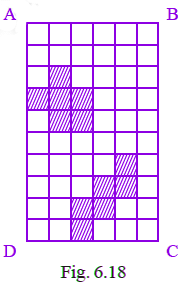
 View Answer
View Answer 
(a) Perimeter of rectangle ABCD = 2(10 + 6) = 120 units.
(b) Area of rectangle ABCD = 10 × 6 = 60 square units.
(c) When the rectangle is divided into 10 equal parts, the area of each part is 6 square units.
(d) Perimeter of each part = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 12 units.
And the perimeter of all parts is equal.
Q42: Rectangular wall MNOP of a kitchen is covered with square tiles of 15cm length (Fig. 6.19). Find the area of the wall.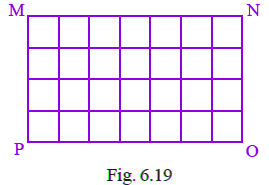
 View Answer
View Answer 
Given, length of square tile = 15 cm
No. of tiles in given figure = 28
Now, area of each tile = 15 × 15 = 225 sq cm
This implies area of 28 tiles = 28 × 225 = 6300 square cm.
Thus, area of wall = 6300 square cm.
Q43: Length of a rectangular field is 6 times its breadth. If the length of the field is 120 cm, find the breadth and perimeter of the field.
 View Answer
View Answer 
Given, Length of a rectangular field = 6 times its breadth.
This implies breadth of the field = Length / 6.
Length of the field = 120 cm.
Thus, breadth = 120 / 6 = 20 cm.
Now, perimeter of the field = 2(l + b) = 2(120 + 20) = 280 cm.
Q44: Anmol has a chart paper of measure 90 cm × 40 cm, whereas Abhishek has one which measures 50 cm × 70 cm. Which will cover more area on the table and by how much?
 View Answer
View Answer 
Area of chart paper of Anmol = 90 × 40 = 3600 square cm
Also, area of chart paper of Abhishek = 50 × 70 = 3500 square cm
Thus, chart paper of Anmol covers more area on the table by = 3600 – 3500 = 100 square cm.
Q45: A rectangular path of 60 m length and 3 m width is covered by square tiles of side 25 cm. How many tiles will there be in one row along its width? How many such rows will be there? Find the number of tiles used to make this path?
 View Answer
View Answer 
Given, length and width of rectangular path = 60 m and 3 m
Also, side of square tile = 25 cm
Thus, no. of tiles in a row = 3 / 0.25 = 12
Now, no. of rows = 60 / 0.25 = 240
Hence, total no. of tiles = 12 × 240 = 2880.
Q46: How many square slabs each with side 90cm are needed to cover a floor of area 81 sqm?
 View Answer
View Answer 
Area of each square slab = 90 × 90 = 8100 square cm
Also, area of floor = 81 square m = 81 × 10000 = 810000 square cm
No. of square slabs required = 810000 / 8100 = 100.
Q47: The length of a rectangular field is 8 m and breadth is 2 m. If a square field has the same perimeter as this rectangular field, find which field has the greater area.
 View Answer
View Answer 
Given, Perimeter of rectangular field = Perimeter of square field
This implies, 2(8 m + 2 m) = 4 × side
Side of square field = 20 / 4 = 5 m
Now, area of rectangular field = 8 × 2 = 16 m²
Area of square field = 5 × 5 = 25 m²
So, the area of the square field is greater than the area of the rectangular field.
Q48: Parmindar walks around a square park once and covers 800m. What will be the area of this park?
 View Answer
View Answer 
Given, perimeter of the park = 800 m
Thus, if the side of the square is a, then 4 × a = 800
a = 200 m
Now, area of the park = 200 × 200 = 40000 m².
Q49: The side of a square is 5cm. How many times does the area increase, if the side of the square is doubled?
 View Answer
View Answer 
Given, side of square = 5 cm
Area of square = 5 × 5 = 25 cm²
Now, side of square becomes = 5 × 2 = 10 cm
Now, area of square = 10 × 10 = 100 cm²
Area increases by = 100 – 25 = 75 cm².
Q50: Amita wants to make rectangular cards measuring 8 cm × 5 cm. She has a square chart paper of side 60 cm. How many complete cards can she make from this chart? What area of the chart paper will be left?
 View Answer
View Answer 
Given, area of the square chart = 60 × 60 = 3600 cm²
Now, area of each card = 8 × 5 = 40 cm²
This implies, No. of cards that can be made = 3600 / 40 = 90 cards.
Q51: A magazine charges Rs 300 per 10 sq cm area for advertising. A company decided to order a half-page advertisement. If each page of the magazine is 15 cm × 24 cm, what amount will the company have to pay for it?
 View Answer
View Answer 
Area of one page of magazine = 15 × 24 = 360 cm²
Thus, area of the half-page of the magazine = 360 / 2 = 180 cm²
Also given, cost of advertising for 10 sq cm = Rs. 300
This implies cost of advertising for 180 sq cm = (300 / 10) × 180 = Rs. 5400.
Q52: The perimeter of a square garden is 48 m. A small flower bed covers 18 sqm area inside this garden. What is the area of the garden that is not covered by the flower bed? What fractional part of the garden is covered by the flower bed? Find the ratio of the area covered by the flower bed and the remaining area.
 View Answer
View Answer 
Given, perimeter of the square garden = 48 m
This implies, 4 × side = 48 m
Side = 48 / 4 = 12 m
Now, area of the square garden = 12 × 12 = 144 m²
Also, area of the small flower bed = 18 m²
So, the area of the garden that is not covered by the flower bed = 144 – 18 = 126 m².
Now, the fractional part of the garden covered by the flower bed = 18 / 144 = 1 / 8.
In addition, the ratio of the area covered by the flower bed and the remaining area = 18 / 126 = 1 / 7 = 1:7.
Q53: Perimeter of a square and a rectangle is the same. If a side of the square is 15cm and one side of the rectangle is 18cm, find the area of the rectangle.
 View Answer
View Answer 
Given, Perimeter of a square = Perimeter of a rectangle
Also, side of square = 15 cm, side of rectangle = 18 cm
Thus, 4 × 15 = 2(18 + b)
b = 30 – 18 = 12 cm
Now, area of the rectangle = 18 × 12 = 216 cm².
Q54: A wire is cut into several small pieces. Each of the small pieces is bent into a square of side 2cm. If the total area of the small squares is 28 square cm, what was the original length of the wire?
 View Answer
View Answer 
Let the number of small pieces in which the wire is cut be x.
Also, given side of each square-shaped piece = 2 cm.
So, Area of each piece = 2 × 2 = 4 cm².
Given total area of the small squares = 28 cm².
Thus, 4x = 28, x = 7.
So, the number of pieces = 7.
It will give the perimeter of each piece with side 2 cm = 4 × 2 = 8 cm.
Therefore, the total length of the wire = 7 × 8 = 56 cm.
Q55: Divide the park shown in Fig. 6.17 of question 40 into two rectangles. Find the total area of this park. If one packet of fertilizer is used for 300sqm, how many packets of fertilizer are required for the whole park?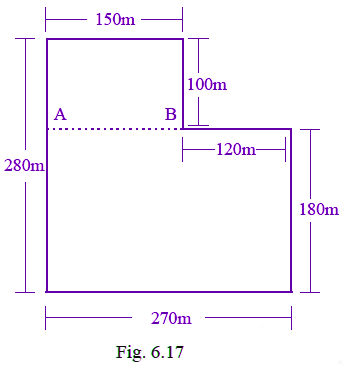
 View Answer
View Answer 
Total area of the park = 15000 + (270 x 180) = 15000 + 48600 = 63600 m2
Now one packet of fertilizer is used for area = 300 m2
Thus, total packets of fertilizer required = 63600 / 300 = 121
Q56: The area of a rectangular field is 1600 sqm. If the length of the field is 80m, find the perimeter of the field.
 View Answer
View Answer 
Given, area of a rectangular field = 1600 m2
And length of field = 80m
Now area of rectangular field is l x b
This implies, 80 x b = 1600
b = 1600 / 80 = 20 m
Now, perimeter of rectangular field = 2(l + b) = 2(80 + 20) = 200 m
Q57: The area of each square on a chess board is 4sq cm. Find the area of the board.
 View Answer
View Answer 
Given, area of one square on a chess board = 4 sq cm
Now there are 64 squares on a chess board.
This implies area of chess board = 64 × 4 cm2 = 256 cm2
(a) At the beginning of the game when all the chess men are put on the board, write the area of the squares left unoccupied.
At the beginning of the game, 32 squares are left unoccupied.
Thus, area of the squares left unoccupied = 32 x 4 cm2 = 128 cm2
(b) Find the area of the squares occupied by chess men.
Area occupied by chess men = 32 x 4 cm2 = 128 cm2
Q58: (a) Find all the possible dimensions (in natural numbers) of a rectangle with a perimeter of 36 cm and find their areas.
(b) Find all the possible dimensions (in natural numbers) of a rectangle with an area of 36 sq cm, and find their perimeters.
 View Answer
View Answer 
(a) Perimeter of the rectangle = 36 cm
2(length + breadth) = 36 cm
Length + breadth = 36/2 = 18 cm
All the possible dimensions (in natural numbers) of a rectangle with a perimeter of 36 cm are:
17 x 1 cm, 16 x 2 cm, 15 x 3 cm, 14 x 4 cm, 13 x 5 cm, 12 x 6 cm, 11 x 7 cm, 10 x 8 cm, 9 x 9 cm respectively.
Their corresponding areas are 17 cm2, 32 cm2, 45 cm2, 56 cm2, 65 cm2, 72 cm2, 77 cm2, 80 cm2, and 81 cm2.
(b) The area of the rectangle = 36 sq cm
length × breadth = 36 sq cm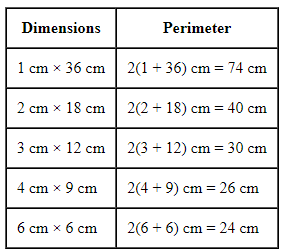
Q59: Find the area and perimeter of each of the following figures, if the area of each small square is 1 sq cm.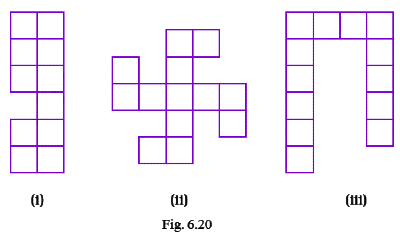
 View Answer
View Answer 
(i) Area of the given figure = 11 x 1 cm2 = 11 cm2
Perimeter of the given figure = 18 x 1 = 18 cm
(ii) Area of the given figure = 13 x 1 cm2 = 13 cm2
Perimeter of the given figure = 28 x 1 = 28 cm
(iii) Area of the given figure = 13 x 1 cm2 = 13 cm2
Perimeter of the given figure = 28 x 1 = 28 cm
Q60: What is the area of each small square in Fig. 6.21 if the area of the entire figure is 96 sq cm? Find the perimeter of the figure.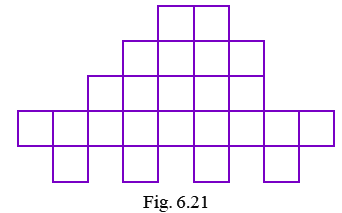
 View Answer
View Answer 
Total number of small squares in the given figure = 24
Area of the total figure = 96 cm2
So, the area of each small square = 96 / 24 = 4 cm2
Now, the side of each small square = 2 cm
Perimeter of the figure = 34 x 2 = 68 cm
|
48 videos|334 docs|23 tests
|
FAQs on NCERT Exemplar Solutions: Mensuration - Mathematics for Class 6
| 1. What is mensuration and why is it important in mathematics? |  |
| 2. What are the basic formulas for finding the area and perimeter of common shapes? |  |
| 3. How do you calculate the volume of 3D shapes in mensuration? |  |
| 4. How can I apply mensuration concepts to real-life situations? |  |
| 5. What are some common mistakes to avoid in mensuration problems? |  |
















