Whole Numbers Class 6 Notes Maths Chapter 2
Introduction
- Natural numbers are used for counting, starting from 1 and going on indefinitely.
- Whole numbers expand on natural numbers by including zero (0) along with all the natural numbers.

- Zero is the smallest whole number, making it the starting point for the set of whole numbers.
- While all natural numbers are part of the set of whole numbers, not every whole number is a natural number because whole numbers include zero, which natural numbers do not.
Predecessor and Successor
- We can obtain the predecessor of a whole number by subtracting 1 from it. Therefore, the number which comes before the given number is known as Predecessor.
Number – 1 = Predecessor

- We can obtain the successor of a whole number by adding 1 to the given number. Therefore, the number which comes after the given number is known as Successor.
Number + 1 = Successor

Example: Write the successor of:
(a) 244068
(b) 100199
(c) 2345670
(d) 99999 Example: Write the predecessor of
Example: Write the predecessor of
(a) 980
(b) 100000
(c) 30809
(d) 7654321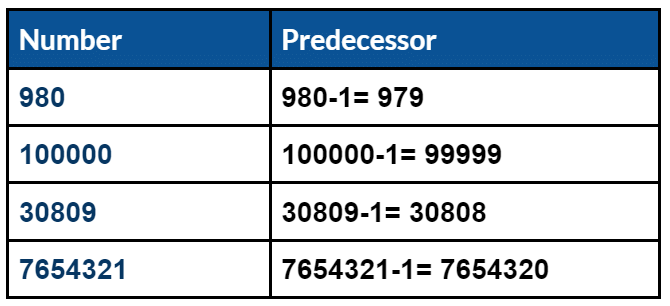
Number Line
- It is the infinitely long line containing all the whole numbers.
- The line starts at zero, and any two consecutive whole numbers have the same distance between them.
How to draw a number line?
Step 1: Draw a line and mark it with a 0 point.
Step 2: Now label the second point to the right of zero as 1.
The distance between the 0 and 1 is called the unit distance.
Step 3: Now you can mark other points as 2, 3, 4 and so on with the unit distance
 Number Line for whole numbers
Number Line for whole numbers
- We can also compare two whole numbers with the help of a number line.
- On the number line we see that the number 6 is on the right of 2.
Therefore, 6 is greater than 2, i.e. 6 > 2.

Facts about whole numbers!
Example: In each of the following pairs of numbers, state which whole number is on the left of the other number on the number line? Also write them with the appropriate sign (>, <) between them.
a) 440, 404
b) 280, 208
Sol: (a) 404 is on the left side of 440. So, 440 > 404
(b) 208 is on the left of 280. So, 208 < 280.
Operations on a Number line
Addition on the Number Line
If we have to add 2 and 5, then start with 2 and make 5 jumps to the right. As our 5th jump is at 7, the answer is 7.

The sum of 2 and 5 is 2 + 5 = 7
Subtraction on the Number Line
If we have to subtract 6 from 10, then we have to start from 10 and make 6 jumps to the left. As our 6th jump is at 4, the answer is 4. The subtraction of 6 from 10 is 10 – 6 = 4.
The subtraction of 6 from 10 is 10 – 6 = 4.Multiplication on the Number Line
If we have to multiply 4 and 3, then start from 0, make 4 jumps using 3 units at a time to the right, as you reach 12. 
So, we say, 3 × 4 = 12.
Division on a number line.
For example 6 ÷ 3 = 2.Start from 6 and subtract 3 for a number of times till 0 is reached. The number of times 3 is subtracted gives the quotient.

Properties of Addition
If we see various operations on numbers, we notice several properties of whole numbers. These properties help us to understand the numbers better and also make calculations under certain operations very simple.
Properties of Addition
1. Closure property
 If 𝒂 and 𝒃 are two whole numbers, then 𝒂 + 𝒃 is always a whole number.
If 𝒂 and 𝒃 are two whole numbers, then 𝒂 + 𝒃 is always a whole number.

Therefore, the sum of any two whole numbers is a whole number. This property is known as the "closure property" for the addition of whole numbers.
2. Commutative property

If 𝒂 and 𝒃 are two whole numbers, then 𝒂 + 𝒃 = 𝒃 + 𝒂

Hence, we can add two whole numbers in any order. So, the sum of whole numbers remains the same even if the order of addition is changed.
Therefore, we can say that addition is commutative for whole numbers. This property is known as commutativity for addition.
3. Associative Property

If 𝒂, 𝒃 & 𝒄 are any three whole numbers, then
(𝒂 + 𝒃) + 𝒄 = 𝒂 + (𝒃 + 𝒄)

When we are adding whole numbers, they can be grouped in any order and the result remains the same. Therefore, whole numbers are associative under addition. This property is known as associativity for addition.

Example: Find the sum of 435, 216 and 165
Sol: 435 + 216 + 165
Now, 5 + 5 = 10. So, we add 435 + 165 first.
= (435 + 165) + 216
= 600 + 216 = 816
Example: Find the sum by suitable arrangement:
(a) 837 + 208 + 363
(b) 1962 + 453 + 1538 + 647
Sol: a) 837 + 208 + 363
Now, 7 + 3 = 10.
So, we add 837 + 363 first.
= (837 + 363) + 208
= 1200 + 208 = 1408
(b) 1962 + 453 + 1538 + 647
Now, 2 + 8 = 10 .So, we make one group of (1962 + 1538)
3 + 7 = 10. Next we make another group of (453 + 647)
= (1962 + 1538) + (453 + 647)
=3500 + 1100 = 4600
4. Additive Identity Property

If 𝒂 is any whole numbers, then 𝒂 + 𝟎 = 𝒂 = 𝟎 + 𝒂

The number 'zero' has a special role in addition. When we add zero to any whole number the result is the same whole number again. Zero is called an identity for addition of whole numbers or additive identity for whole numbers.
Properties of Subtraction
Subtraction is an inverse process of addition.
Example: (7 + 2 = 9) ⇒ (9 – 7 = 2)

1. Closure Property

If 𝒂 and 𝒃 are two whole numbers such that 𝒂 > 𝑏 or 𝒂 = 𝒃, then 𝒂 − 𝒃 is a whole number.
If 𝒂 < 𝑏, then 𝒂 − 𝒃 is not a whole number.


The whole numbers are not closed under subtraction.
2. Commutative Property

If 𝒂 and 𝒃 are two whole numbers, then 𝒂 − 𝒃 ≠ 𝒃 − 𝒂

3. Associative Property

For any three whole numbers 𝒂, 𝒃 and 𝒄, (𝒂 – 𝒃) – 𝒄 ≠ 𝒂 – (𝒃 – 𝒄)

(iv) If 𝒂 is any whole number other than zero, then 𝒂 – 𝟎 = 𝒂 but 𝟎 − 𝒂 is not defined.
30 – 12 = 18 but 12 – 30 is not defined in whole numbers
(v) If 𝒂, 𝒃 and 𝒄 are whole numbers such that 𝒂 – 𝒃 = 𝒄, then 𝒃 + 𝒄 = 𝒂
 Transposing 𝒃 to RHS,
Transposing 𝒃 to RHS,𝒂 = 𝒄 + 𝒃 or 𝒂 = 𝒃 + 𝒄
If 25 – 16 = 9 then 25 = 9 + 16,
If 46 – 8 = 38 then 46 = 38 + 8
Example: Consider two whole numbers 𝒑 and 𝒒 such that 𝒑 is greater than 𝒒.
1. Is 𝒑 − 𝒒 a whole number? Is the result always true?
2. Is 𝒒 − 𝒑 a whole number? Is the result always true?
Sol: 1. Yes, 𝒑 − 𝒒 is a whole number is always true for 𝒑 > 𝑞.
2. No, 𝒒 − 𝒑 is not a whole number is always true for 𝒑 > 𝑞.
Let the value of 𝒑 and 𝒒 be 10 and 7 respectively.

𝒑 − 𝒒 = 10 – 7 = 3, a whole number 𝒒 − 𝒑 = 7 – 10 not a whole number
𝒒 − 𝒑 = 7 – 10 not a whole number
Example: Solve the following:
i) 367 – 99
367 – 99
= 367 + (– 100 + 1)
= 367 – 100 + 1
= (367 + 1) – 100
= 368 – 100
= 268
ii) 5689 – 99
5689 – 99
= 5689 + (- 100 +1)
= 5689 – 100 + 1
= (5689 + 1) – 100
= 5690 – 100
= 5590
Properties of Multiplication
Let us consider 3 packets, each consisting of 4 doughnuts.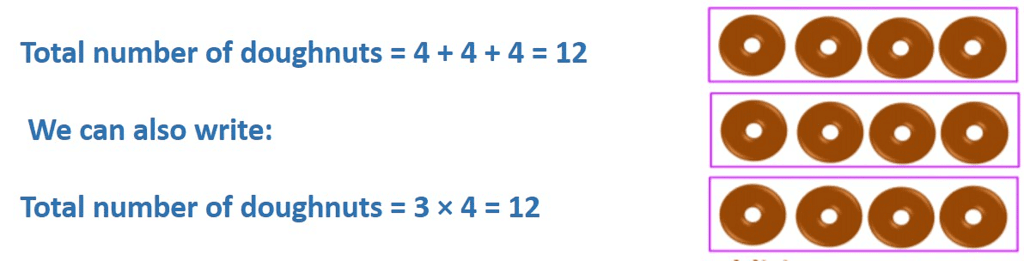 Therefore, we can say that multiplication is repeated addition.
Therefore, we can say that multiplication is repeated addition.1. Closure Property:
 If 𝒂 and 𝒃 are two whole numbers, then 𝒂 × 𝒃 is always a whole number.
If 𝒂 and 𝒃 are two whole numbers, then 𝒂 × 𝒃 is always a whole number. 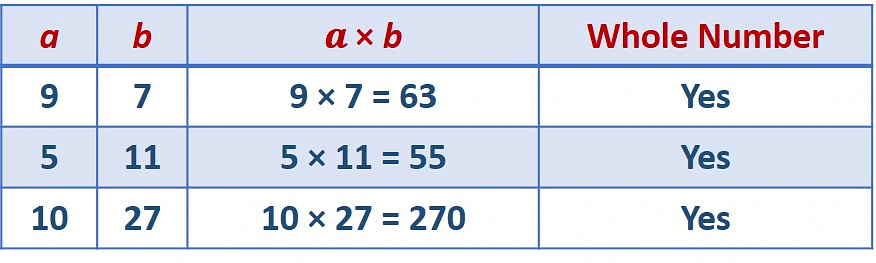

When we multiply two whole numbers, the product is also a whole number.
2. Commutative Property

If 𝒂 and 𝒃 are two whole numbers, then 𝒂 × 𝒃 = 𝒃 × 𝒂  The value of the product does not change even when the order of multiplication is changed.
The value of the product does not change even when the order of multiplication is changed.
3. Associative Property
 If 𝒂, 𝒃&𝒄 are any three whole numbers, then
If 𝒂, 𝒃&𝒄 are any three whole numbers, then (𝒂 × 𝒃) × 𝒄 = 𝒂 × (𝒃 × 𝒄) 
When we multiply three or more whole numbers, the value of the product remains the same even if they are grouped in any manner.
4. Multiplicative Identity Property
 If 𝒂 is any whole number, then 𝒂 × 𝟏 = 𝒂 = 𝟏 × 𝒂
If 𝒂 is any whole number, then 𝒂 × 𝟏 = 𝒂 = 𝟏 × 𝒂  Multiplicative identity is any number which when multiplied by any whole number, then the value remains the same.
Multiplicative identity is any number which when multiplied by any whole number, then the value remains the same.So, 1 is the multiplicative identity of whole numbers.
5. Distributivity of Multiplication over Addition:
 If 𝒂, 𝒃&𝒄 are any three whole numbers, then
If 𝒂, 𝒃&𝒄 are any three whole numbers, then 𝒂 × (𝒃 + 𝒄) = 𝒂 × 𝒃 + 𝒂 × 𝒄

6. If 𝒂 is any whole number other than zero, then 𝒂 × 𝟎 = 𝟎

15 × 0 = 0; 100 × 0 = 0
Example: Find the product by suitable rearrangement:
i) 4 × 1768 × 25
ii) 2 × 166 × 50
iii) 285 × 4 × 75
iv) 625 × 279 × 16
Ans.
i) 4 × 1768 × 25= (4 × 25) × 1768 (by commutative property)
= 100 × 1768 = 176800
ii) 2 × 166 × 50= (2 × 50) × 166 (by commutative property)
= 100 × 166 = 16600
iii) 285 × 4 × 75= 285 × (4 × 75) (by commutative property)
= 285 × 300 = 85500
iv) 625 × 279 × 16= (625 × 16) × 279 (by commutative property)
= 10000 × 279 = 2790000
Example: A taxi driver filled his car petrol tank with 40 liters of petrol on Monday. The next day, he filled the tank with 60 liters of petrol. If the petrol costs Rs 45 per liter, how much did he spend in all on petrol?
Sol:Petrol filled on Monday = 40 liters
Petrol filled on Tuesday = 60 liters
Total petrol filled = (40 + 60) liters
Cost of 1 liter of petrol = Rs 45
Cost of 90 liters of petrol = Rs 454× (40 + 60)
= Rs 45 × (40 + 60)
= Rs 45 × 100
= Rs 4500
Properties of Division
1. Closure Property
 If a and b are two whole numbers, then a ÷ b is not always a whole number.
If a and b are two whole numbers, then a ÷ b is not always a whole number. So, whole numbers are not closed under division.
So, whole numbers are not closed under division.
2. Commutative Property
 If a and b are two whole numbers, a ÷ b ≠ b ÷ a
If a and b are two whole numbers, a ÷ b ≠ b ÷ a
3. Associative Property

For any 3 whole numbers a, b and c,
(a ÷ b) ÷ c ≠ a ÷ (b ÷ c)

So, division of whole numbers is not Associative.
(iv) Division by 1
 If a is a whole number, then a ÷ 1 = a
If a is a whole number, then a ÷ 1 = a
(v) Division of 0 by any whole number
 If a is any whole number other than zero, then 0 ÷ a = 0
If a is any whole number other than zero, then 0 ÷ a = 0 If we divide 0 by any whole number, the result is always 0.
If we divide 0 by any whole number, the result is always 0.(vi) Division of any whole number by 0
 To divide any number, say 6 by 0, we first have to find out a whole number which when multiplied by 0 gives us 6. This is not possible.
To divide any number, say 6 by 0, we first have to find out a whole number which when multiplied by 0 gives us 6. This is not possible.Therefore, division by 0 is not defined.
Example: Solve the following
(i) 636 ÷ 1
(ii) 0 ÷ 253
(iii) 246 – (121 ÷ 121)
(iv) (45÷ 5) – (9÷ 3)
Sol: (i) 636 ÷ 1 = 636 (∵ a ÷1 = a )
(ii) 0 ÷ 253 = 0 (∵ 0 ÷ a = 0)
(iii) 246 – (121 ÷ 121)
= 246 – (1)
= 246 – 1
= 245
(iv) (45÷ 5) – (9 ÷ 3)
= 9 – 3 = 6
|
92 videos|348 docs|54 tests
|
FAQs on Whole Numbers Class 6 Notes Maths Chapter 2
| 1. What are some key properties of addition for whole numbers? |  |
| 2. How can whole numbers be represented on a number line? |  |
| 3. What are some important facts about whole numbers? |  |
| 4. What are the properties of multiplication for whole numbers? |  |
| 5. How can operations on a number line help in understanding whole numbers better? |  |





















