NCERT Exemplar: Sets- 1 | Mathematics (Maths) Class 11 - Commerce PDF Download
SHORT ANSWER TYPE QUESTIONS
Q.1. Write the following sets in the roaster from
(i) A = {x : x ∈ R, 2x + 11 = 15}
(ii) B = {x | x2 = x, x ∈ R}
(iii) C = {x | x is a positive factor of a prime number p}
Ans.
(i) Given that: A = {x : x ∈ R, 2x + 11 = 15}
∴ 2x + 11 = 15
⇒ 2x = 15 - 11
⇒ 2x = 4
⇒ x = 2
Hence, A = {2}
(ii) Given that: B = {x|x2 = x, x ∈ R}
∴ x2 = x
⇒ x2 - x = 0
⇒ x(x - 1)=0
∴ x = 0, x = 1
Hence,
B = {0, 1}
(iii) Given that: C = {x|x is a positive factor of a prime number P} So, the positive factors of prime number P are 1 and P.
Hence,
C = {1, P}
Q.2. Write the following sets in the roaster form:
(i) D = {t | t3 = t, t ∈ R}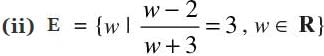
(iii) F = {x | x4 – 5x2 + 6 = 0, x ∈ R}
Ans.
(i) Given that: D = {t|t3=t, t ∈ R}
∴ t3 = t
⇒ t3 - t = 0
⇒ t (t2-1) = 0
⇒ t (t - 1) (t + 1) = 0
⇒ t = 0, t = 1, t = -1
Hence, D = {-1, 0, 1}
(ii) Given that: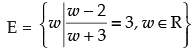
∴ 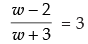
⇒ 3w + 9= w - 2
⇒ 3w - w = - 2 - 9
⇒ 2w = -11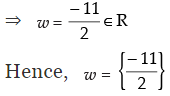
(iii) Given that: F = {x|x4-5x2+6= 0, x ∈ R}
∴ x4 - 5x2 + 6 = 0
⇒ x4 - 3x2 - 2x2 + 6 = 0
⇒ x2(x2 - 3) - 2(x2 - 3) = 0
⇒ (x2 - 2)(x2 - 3) = 0
⇒ x2 - 2 = 0 and x2 - 3 = 0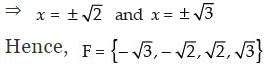
Q.3. If Y = {x | x is a positive factor of the number 2p – 1 (2p – 1), where 2p – 1 is a prime number}.Write Y in the roaster form.
Ans. Given that:
Y= {x|x is a positive factor of the number 2P-1(2P-1)}
The factors of 2P-1 are 1, 2, 22, 23, 24, …, 2P-1
The factors of (2P-1) are 1,(2P- 1)[The positive factors of prime number P are 1 and P]
Hence, Y= {1, 2, 22, 23, 24, …, 2P-1,(2P-1)}
Q.4. State which of the following statements are true and which are false. Justify your answer.
(i) 35 ∈ {x | x has exactly four positive factors}.
(ii) 128 ∈ {y | the sum of all the positive factors of y is 2y}
(iii) 3 ∉ {x | x4 – 5x3 + 2x2 – 112x + 6 = 0}
(iv) 496 ∉ {y | the sum of all the positive factors of y is 2y}.
Ans.
(i) Given that : 35 ∈ {x|x has exactly four positive factors} ∴ Factors of 35 are 1, 5, 7, 35
Hence, the statement (i) is ‘True’.
(ii) Given that: 128 ∈ {y| the sum of all positive factors of y is 2y} ∴ Factors of 128 are 1, 2, 4, 8, 16, 32, 64, 128.
Sum of all the factors =1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 = 255 ≠ 2 × 128
Hence, the given statement is ‘False’.
(iii) Given that: 3 ∉ {x|x4 - 5x3 + 2x2 - 112x + 6 = 0}
∴ x4 - 5x3 + 2x2 - 112x + 6 = 0
Now for x = 3, we have
(3)4 - 5(3)3 + 2(3)2 - 112(3) + 6 = 0
⇒ 81 - 135 + 18 - 336 + 6 = 0
⇒ -366 = 0 which is not true.
So 3 cannot be an element of the given set.
Hence, statement (iii) is ‘True’.
(iv) Given that: 496 ∉ {y| the sum of all the positive factor of y is 2y} ∴ The positive factors of 496 are 1, 2, 4, 8, 16, 31, 62, 124, 248 and 496 ∴ The sum of all the positive factor of 496
= 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 + 496 = 992 = 2 × 496
So 496 is an element of the given set.
Hence, the given statement is ‘False’.
Q.5. Given L = {1, 2, 3, 4}, M = {3, 4, 5, 6} and N = {1, 3, 5}
Verify that L – (M ∪ N) = (L – M) ∩ (L – N)
Ans. Given that: L = {1, 2, 3, 4}, M = {3, 4, 5, 6} and N = {1, 3, 5}
To verify that L - (M ∪ N) = (L - M) ∩ (L - N)
L.H.S. = L - (M ∪ N) = {1, 2, 3, 4} - {{3, 4 , 5, 6} ∪ {1, 3, 5}}
= {1, 2, 3, 4} - {1, 3, 4, 5, 6} = {2}
R.H.S. = (L - M) ∩ (L - N)
(L - M) = {1, 2, 3, 4} - {3,4,5,6} = {1, 2}
(L - N) = {1, 2, 3, 4} - {1, 3, 5} = {2, 4}
∴ (L - M) ∩ (L - N) = {1, 2} ∩ {2, 4} = {2}
L.H.S. = R.H.S.
Hence, verified.
Q.6. If A and B are subsets of the universal set U, then show that
(i) A ⊂ A ∪ B
(ii) A ⊂ B ⇔ A ∪ B = B
(iii) (A ∩ B) ⊂ A
Ans.
(i) Given that: A ⊂ U and B ⊂ U
To prove A⊂A ∪ B it is enough to show that if x ∈ A ⇒ x∈ A∪ B
Let x ∈ A
⇒ x ∈ A or x ∈ B
⇒ x ∈ A ∪ B
Hence, A ⊂ (A ∪ B)
(ii) If A ⊂ B
Then let x ∈ A ∪ B
⇒ x ∈ A or x ∈ B
⇒ x ∈ B [∵ A ⊂ B]
⇒ A ∪ B ⊂ B ….(1)
But B ⊂ A ∪ B ….(2)
From eqn. (1) and (2), we get
A ∪ B=B.
Now if A ∪ B=B
Let y ∈ A
⇒ y ∈ (A ∪ B)
⇒ y ∈ B [∵A ∪ B =B]
Hence A ⊂ B
So we proved A ⊂ B ⇔ A ∪ B=B
(iii) Let x ∈ A ∩ B
⇒ x ∈ A and x ∈ B
⇒ x ∈ A
So, A ∩ B ⊂ A.
Q.7. Given that
N = {1, 2, 3, ... , 100}. Then write
(i) the subset of N whose elements are even numbers.
(ii) the subset of N whose element are perfect square numbers.
Ans. We are given that: N= {1, 2, 3, 4, 5, …, 100}
(i) Required subset whose elements are even
= {2, 4, 6, 8,10,12,........…,100}
(ii) Required subset whose elements are perfect squares
= {1, 4, 9, 16, 25, 36,49,64,81,100}
Q.8. If X = {1, 2, 3}, if n represents any member of X, write the following sets containing all numbers represented by
(i) 4n
(ii) n + 6
(iii) n/2
(iv) n – 1
Ans.
Given that: X = {1, 2, 3}
(i) {4n|n ∈ X} = {4, 8, 12}
(ii) {n+6|n ∈ X} = {7, 8, 9}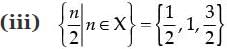
(iv) {(n-1)|n ∈ X} = {0, 1, 2}
Q.9. If Y = {1, 2, 3, ... 10}, and a represents any element of Y, write the following sets, containing all the elements satisfying the given
conditions.
(i) a ∈ Y but a2 ∉ Y
(ii) a + 1 = 6, a ∈ Y
(iii) a is less than 6 and a ∈ Y
Ans. Given that: Y = {1, 2, 3, …, 10}
(i) {a|a ∈ Y but a2 ∉ Y} = {4, 5, 6, 7, 8, 9, 10}
(ii) {a|a + 1 = 6, a ∈ Y} = {5}
(iii) {a|a < 6 and a ∈ Y} = {1, 2, 3, 4, 5}
Q.10. A, B and C are subsets of Universal Set U. If A = {2, 4, 6, 8, 12, 20} B = {3, 6, 9, 12, 15}, C = {5, 10, 15, 20} and U is the set of all whole numbers, draw a Venn diagram showing the relation of U, A, B and C.
Ans. Given that: A, B, and C are the subsets of a universal set U.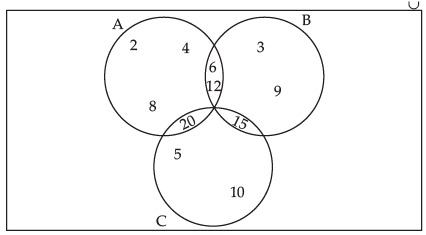 Where A = {2, 4, 6, 8, 12, 20}
Where A = {2, 4, 6, 8, 12, 20}
B = {3, 6, 9, 12, 15}
and C = {5, 10, 15, 20}
Q.11. Let U be the set of all boys and girls in a school, G be the set of all girls in the school, B be the set of all boys in the school, and S be the set of all students in the school who take swimming. Some, but not all, students in the school take swimming. Draw a Venn diagram showing one of the possible interrelationship among sets U, G, B and S.
Ans. Given that:
U = Set of all boys and girls.
G = Set of girls
B = Set of boys
S = Set of all students, who take swimming.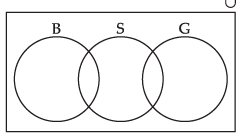
Q.12. For all sets A, B and C, show that (A – B) ∩ (C – B) = A – (B ∪ C)
Ans. To prove (A - B) ∩ (A - C) = A - (B ∪ C).
Let x ∈ (A - B) ∩ (A - C)
⇒ x ∈ (A - B) and x ∈ (A - C)
⇒ (x ∈ A and x ∉ B) and (x ∈ A and x ∉ C)
⇒ x ∈ A and (x ∉ B and x ∉ C)
⇒ x ∈ A and x ∉ (B ∪ C)
⇒ x ∈ A - (B ∪ C)
So (A - B) ∩ (A - C) ⊂ A - (B ∪ C) ….(i)
Let y ∈ A - (B ∪ C)
⇒ y ∈ A and y ∉ (B ∪ C)
⇒ y ∈ A and (y ∉ B and y ∉ C)
⇒ (y ∈ A and y ∉ B) and (y ∈ A and y ∉ C)
⇒ y ∈ (A - B) and y ∈ (A - C)
⇒ y ∈ (A - B) ∩ (A - C)
So, A - (B ∪ C) ⊂ (A - B) ∩ (A - C) …(ii)
From eqn. (i) and (ii),we get
A - (B ∪ C) = (A - B) ∩ (A - C)
Q.13. For all sets A and B, (A – B) ∪ (A ∩ B) = A
Ans. L.H.S. = (A - B) ∪ (A ∩ B)
= [(A - B) ∪ A] ∩ [(A - B) ∪ B]
= A∩(A∪B) = A = R.H.S.
Hence, the given statement is ‘True’.
Q.14. For all sets A, B and C, A – (B – C) = (A – B) – C
Ans. Let us solve the given statement by the following Venn diagram.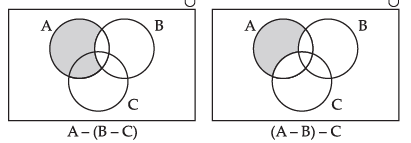
Clearly from the above diagram, we calculate that
A - (B - C) ≠ (A - B) - C
Hence, the given statements is not ‘True’.
Q.15. For all sets A, B and C, if A ⊂ B, then A ∩ C ⊂ B ∩ C
Ans. Suppose A ⊂ B
Let x ∈ A ∩ C
⇒ x ∈ A or x ∈ C
⇒ x ∈ B or x ∈ C [∵ A ⊂ B]
⇒ x ∈ (B ∩ C)
⇒(A ∩ C) ⊂ (B ∩ C)
Hence, the given statement is ‘True’.
Q.16. For all sets A, B and C, if A ⊂ B, then A ∪ C ⊂ B ∪ C
Ans. Suppose A ⊂ B
Let x ∈ A ∪ C
⇒ x ∈ A or x ∈ C
⇒ x ∈ B or x ∈ C [∵ A ⊂ B]
⇒ x ∈ (B ∪ C)
⇒ (A ∪ C) ⊂ (B ∪ C)
Hence, the given statement is ‘True’.
Q.17. For all sets A, B and C, if A ⊂ C and B ⊂ C, then A ∪ B ⊂ C.
Ans. Suppose A ⊂ C and B ⊂ C
Let x ∈ A ∪ B
⇒ x ∈ A or x ∈ B
⇒ x ∈ C or x ∈ C [∵ A ⊂ C and B ⊂ C]
⇒ x ∈ C ⇒ A ∪ B ⊂ C
Hence, the given statement is ‘True’.
Q.18. For all sets A and B, A ∪ (B – A) = A ∪ B
Ans. L.H.S.= A∪ (B - A) = A∪ (B ∩ A’) [∵ A - B = A ∩ B’]
= (A ∪ B) ∩ (A ∪ A’) [distributive law]
= (A ∪ B) ∩U = (A ∪ B) U [∵A∪A’ = U]
= (A ∪ B) = R.H.S [∵ A ∩ U = A]
Hence, the given statement is proved.
Q.19. For all sets A and B, A – (A – B) = A ∩ B
Ans. L.H.S. = A - (A - B) = A - (A ∩ B’) [∵A - B = A ∩ B’]
=A ∩ (A ∩ B’)’= A ∩ [A’∪ (B’)’] [∵(A ∩ B)’= A’ ∪ B’]
=A ∩ (A’ ∪ B) [∵(A’)’ = A]
=(A ∩ A’) ∪ (A ∩ B) = Φ ∪ (A ∩ B) [A ∩ A’ = Φ ]
=A ∩ B = R.H.S.
L.H.S. = R.H.S. Hence proved.
Q.20. For all sets A and B, A – (A ∩ B) = A – B
Ans. L.H.S.= A - (A ∩ B) = A ∩ (A ∩ B)’ [∵A - B = A ∩ B’]
= A ∩ (A’ ∪ B’) [∵ (A ∩ B)’ = A’ ∪ B’]
= (A ∩ A’) ∪ (A ∩ B’) [ distributive law]
= Φ ∪ (A - B) [∵A ∩ A’= Φ and A - B = A ∩ B’]
= (A - B) = R.H.S.
L.H.S. = R.H.S. Hence proved.
Q.21. For all sets A and B, (A ∪ B) – B = A – B
Ans. L.H.S.(A ∪ B) - B
= (A ∪ B) ∩ B’ [∵ A - B = A ∩ B’]
= (A ∪ B’) ∩ (B ∪ B’) [distributive law]
= (A - B) ∪ Φ [∵ A ∩ A’ = Φ and A - B = A ∩ B’]
= (A - B) = R.H.S.
L.H.S. = R.H.S.
Hence proved.
Q.22. 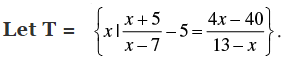
Is T an empty set? Justify your answer.
Ans.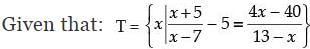
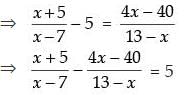

⇒ – 5x2 + 76x – 215 = 5 (13x – x2 + 7x – 91)
⇒ – 5x2 + 86x – 215 = 65x – 5x2 + 35x – 455
⇒ 76x – 100x = –455 + 215
⇒ 24x = -240
x = 240/24 = 10
∴ T = 10
Hence, T is not an empty set.
LONG ANSWER TYPE QUESTIONS
Q.23. Let A, B and C be sets. Then show that A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
Ans. Let x ∈ A ∩ (B ∪ C)
⇒ x ∈ A and x ∈ (B ∪ C)
⇒ x ∈ A and (x ∈ B or x ∈ C)
⇒ (x ∈ A and x ∈ B) or (x ∈ A and x ∈ C)
⇒ (x ∈ A ∩ B) or (x ∈ A ∩ C)
⇒ x ∈ (A ∩ B) ∪ (A ∩ C)
⇒ A ∩ (B ∪ C) ⊂ (A ∩ B) ∪ (A ∩ C).................(i)
Now let y ∈ (A ∩ B) ∪ (A ∩ C)
⇒ y ∈ (A ∩ B) or y ∈ (A ∩ C)
⇒ (y ∈ A and y ∈ B) or (y ∈ A and y ∈ C)
⇒ y ∈ A and (y ∈ B or y ∈ C)
⇒ y ∈ A and y ∈ (B ∪ C)
⇒ y ∈ A ∩ (B ∪ C)
⇒(A ∩ B) ∪ (A ∩ C) ⊂ A ∩ (B ∪ C)…..........................(ii)
From eqn. (i) and (ii) we get
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
Hence proved.
Q.24. Out of 100 students; 15 passed in English, 12 passed in Mathematics, 8 in Science, 6 in English and Mathematics, 7 in Mathematics and Science; 4 in English and Science; 4 in all the three. Find how many passed
(i) in English and Mathematics but not in Science
(ii) in Mathematics and Science but not in English
(iii) in Mathematics only
(iv) in more than one subject only
Ans. Let the number of students passed in Mathematics M, E be in English and S be in Science.
Then n(U) = 100, n(M) = 12, n(E) = 15, n(S) = 8, n(E ∩ M) = 6, n(M ∩ S) = 7, n(E ∩ S) = 4 and n(E ∩ M ∩ S)=4
Let us draw a Venn diagram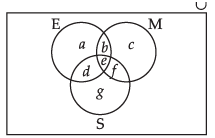 According to the Venn diagram
According to the Venn diagram
n(E ∩ M ∩ S)= 4
⇒ e = 4
n(E ∩ M) = 6
⇒ b + e = 6
⇒ b + 4 = 6
⇒ b=2
n(M ∩ S) = 7
⇒ e + f = 7
⇒ 4 + f =7
⇒ f = 3
n(E ∩ S) = 4
⇒ d + e = 4
⇒ d + 4 = 4
⇒ d = 0
n(E) = 15
⇒ a + b + d + e = 15
⇒ a + 2 + 0 + 4 = 15
⇒ a = 9
n(M) = 12
⇒ b + c + e + f = 12
⇒ 2 + c + 4 + 3 = 12
⇒ c = 3
n(S) = 8
⇒ d + e + f + g = 8
⇒ 0 + 4 + 3 + g = 8
⇒ g = 1
Hence we get,
(i) Number of students who passed in English and Mathematics but not in Science, b = 2.
(ii) Number of students who passed in Mathematics and Science but not in English, f = 3.
(iii) Number of students who passed in Mathematics only, c = 3.
(iv) Number of students who passed in more than one subject = b + e + d + f = 2 + 4 + 0 + 3 = 9.
Q.25. In a class of 60 students, 25 students play cricket and 20 students play tennis, and 10 students play both the games. Find the number of students who play neither?
Ans. Total number of students = 60 ⇒ n(U) = 60
Number of students who play cricket = 25 ⇒ n(C) = 25
Number of students who play tennis = 20 ⇒ n(T) = 20
Number of students who play both the games = 10 ⇒ n(C ∩ T) = 10
∴ Number of students who play any one game = n(C ∪ T) = n(C) + n(T) – n(C ∩ T) = 25 + 20 – 10 = 35
Number of students who play neither
= n(U) – n(C ∪ T)
= 60 – 35 = 25
Q.26. In a survey of 200 students of a school, it was found that 120 study Mathematics, 90 study Physics and 70 study Chemistry, 40 study Mathematics and Physics, 30 study Physics and Chemistry, 50 study Chemistry and Mathematics and 20 none of these subjects. Find the number of students who study all the three subjects.
Ans. Let the set of students who study Mathematics be M, the set of students who study Physics be P and the set of students who study Chemistry be C.
According to the question,
n(U) = 200, n(M)= 120, n(P) = 90, n(C) = 70, n(M ∩ P) = 40, n(P ∩ C) = 30, n(C ∩ M) = 50, and n(M’ ∩ P’ ∩ C’) = 20
∴ n(U) – n(M’ ∩ P’ ∩ C’) = n(M ∪ P ∪ C) = 200 - 20 = 180
Now n(M ∪ P ∪ C) = n(M) + n(P) + n(C) – n(M ∩ P) – n(P ∩ C)– n(M ∩ C) + (n(M ∩ P ∩ C)
⇒ 180 = 120 + 90 + 70 – 40 – 30 – 50 + n(M ∩ P ∩ C)
⇒ 180 – 160 = n(M ∩ P ∩ C)
⇒ n(M ∩ P ∩ C) = 20
Hence, the number of students who study all the three subjects = 20.
Q.27. In a town of 10,000 families it was found that 40% families buy newspaper A, 20% families buy newspaper B, 10% families buy newspaper C, 5% families buy A and B, 3% buy B and C and 4% buy A and C. If 2% families buy all the three newspapers. Find
(a) The number of families which buy newspaper A only.
(b) The number of families which buy none of A, B and C
Ans. Let A denote the set of families which buy newspaper A, B denote the set of families which buy newspaper B and C denote the set of families which buy newspaper C.
According to the question,
n(U) = 10000, n(A) = 40%, n(B) = 20%, n(C) = 10%,
n(A ∩ B) = 5%, n(B ∩ C) = 3%, n(A ∩ C) = 4% and n(A ∩ B ∩ C) = 2%.
(i) Number of families which buy newspaper A only = n(A) – n(A ∩ B) –
n(A ∩ C) + n(A ∩ B ∩ C)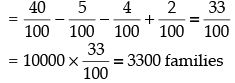
(ii) Number of families which buy none of A, B and C = n(U) – n(A ∪ B ∪ C)
⇒ n(U) – [n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(A ∩ C) + n(A ∩ B ∩ C)]
⇒ [100 - (40 + 20 + 10 – 5 – 3 – 4 + 2)]%
⇒ (100 – 60) % = 40%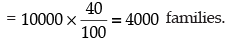
Q.28. In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows: French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study
(i) French only
(ii) English only
(iii) Sanskrit only
(iv) English and Sanskrit but not French
(v) French and Sanskrit but not English
(vi) French and English but not Sanskrit
(vii) at least one of the three languages
(viii) none of the three languages
Ans. Let F be the set of students who study French, E be the set of students who study
English and S be the set of students who study Sanskrit.
Let us use Venn diagram method.
According to the question, n(U)= 50, n(F) = 17, n(E) = 13, n(S) =15, n(F ∩ E) = 9, n(E ∩ S) = 4, n(F ∩ S) = 5 and n(F ∩ E ∩ S) = 3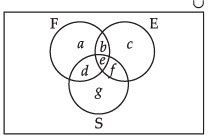
n(E ∩ F ∩ S) = 3
⇒ e = 3
n(F ∩ E) = 9
⇒ b + e = 9
⇒ b + 3 = 9
⇒ b =6.
n(F ∩ S) = 5
⇒ d + e = 5
⇒ d + 3 = 5
⇒ d = 2.
n(E ∩ S) = 4
⇒ e + f = 4
⇒ 3 + f = 4
⇒ f = 1.
n(F) = 17
⇒a + b + d + e = 17
⇒ a + 6 + 2 + 3 = 17
⇒ a = 6. n(E) = 13
⇒ b + c + e + f = 13
⇒ 6 + c + 3 + 1 = 13
⇒ c = 3. n(S) = 15
⇒ d + e + f + g = 15
⇒ 2 + 3 + 1 + g = 15
⇒ g = 9
(i) Number of students who study French only, a = 6
(ii) Number of students who study English only, c = 3
(iii) Number of students who study Sanskrit only, g = 9
(iv) Number of students who study English and Sanskrit but not French, f = 1
(v) Number of students who study French and Sanskrit but not English, d = 2
(vi) Number of students who study French and English but not Sanskrit, b = 6
(vii) Number of students who study at least one of the three languages
= a + b+ c + d + e + f + g
= 6 + 6 + 3 + 2 + 3 +1 + 9 = 30
(viii) Number of students who study none of the three language = 50 – 30 = 20.
|
80 videos|315 docs|99 tests
|
FAQs on NCERT Exemplar: Sets- 1 - Mathematics (Maths) Class 11 - Commerce
| 1. What is a set in mathematics? |  |
| 2. What are the different ways to represent a set? |  |
| 3. What is the cardinality of a set? |  |
| 4. What is the intersection of two sets? |  |
| 5. What is the power set of a set? |  |






















