NCERT Solutions for Class 8 Maths - Squares and Square Roots- 1
| Table of contents |

|
| Try These |

|
| Exercise 6.1 |

|
| Finding the Square of a number |

|
| Pythagorean Triplets |

|
| Exercise 6.2 |

|
| Square Roots |

|
| Think, Discuss and Write |

|
Q.1. Find the perfect square numbers between
(i) 30 and 40
(ii) 50 and 60.
Solution.
(i) Since,
⇒ 1 *1 = 1
⇒ 2 * 2 = 4
⇒ 3 * 3 = 9
⇒ 4 * 4 = 16
⇒ 5 * 5 = 25
⇒ 6 * 6 = 36
⇒ 7 * 7 = 49
Thus, 36 is a perfect square number between 30 and 40.
(ii) Since, 7 * 7 = 49 and 8 * 8 = 64.
It means there is no perfect number between 49 and 64, and thus there is no perfect number between 50 and 60.
Q.2. Can we say whether the following numbers are perfect squares? How do we know?
(i) 1057
(ii) 23453
(iii) 7928
(iv) 222222
(v) 1069
(vi) 2061
Write five numbers which you can decide by looking at their one’s digit that they are not square numbers.
Solution.
(i) 1057
- The ending digit is 7 (which is not one of 0, 1, 4, 5, 6, or 9)
- 1057 cannot be a square number.
(ii) 23453
- The ending digit is 3 (which is not one of 0, 1, 4, 5, 6, and 9).
- 23453 cannot be a square number.
(iii) 7928
- The ending digit is 8 (which is not one of 0, 1, 4, 5, 6 and 9).
- 7928 cannot be a square number.
(iv) 222222
- The ending digit is 2 (which is not one of 0, 1, 4, 5, 6 or 9).
- 222222 cannot be a square number.
(v) 1069
- The ending digit is 9.
- It may or may not be a square number.
Also,
- 30 * 30 = 900
- 31 * 31 = 961
- 32 * 32 = 1024
- 33 * 33 = 1089
i.e. No natural number between 1024 and 1089 is a square number.
∴ 1069 cannot be a square number.
(vi) 2061
- The ending digit is 1
- It may or may not be a square number.
45 * 45 = 2025
and 46 * 46 = 2116
i.e. No natural number between 2025 and 2116 is a square number.
∴ 2061 is not a square number.
We can write many numbers which do not end with 0, 1, 4, 5, 6 or 9. (i.e. which are not square number).
Five such numbers can be:
1234, 4312, 5678, 87543, 1002007.
Q.3. Write five numbers that you cannot decide just by looking at their unit’s digit (or one’s place) whether they are square numbers or not.
Solution. Any natural number ending in 0, 1, 4, 5, 6 or 9 can be or cannot be a square-number.
Five such numbers are:
56790, 3671, 2454, 76555, 69209
Property 1. If a number has 1 or 9 in the unit’s place, then its square ends in 1.
Example: (1)2 = 1, (9)2 = 81, (11)2 = 121, (19)2 = 361, (21)2 = 441.
Q.4. Which of 1232, 772, 822, 1612, 1092 would end with digit 1?
Solution. The squares of those numbers end in 1 which ends in either 1 or 9.
∴ The squares of 161 and 109 would end in 1.
Property 2. When a square number ends in 6, then the number whose square it will have 4 or 6 in its unit place.
Q.5. Which of the following numbers would have digit 6 at unit place.
(i) 192
(ii) 242
(iii) 262
(iv) 362
(v) 342
Solution.
(i) 192: Unit’s place digit = 9
∴ 192 would not have unit’s digit as 6.
(ii) 242: Unit’s place digit = 4
∴ 242 would have unit’s digit as 6.
(iii) 262: Unit’s place digit = 6
∴ 262 would have 6 as unit’s place.
(iv) 362: Unit place digit = 6
∴ 362 would end in 6.
(v) 342: Since the unit place digit is 4
∴ 342 would have unit place digit as 6.
Q.6. What will be the “one’s digit” in the square of the following numbers?
(i) 1234
(ii) 26387
(iii) 52698
(iv) 99880
(v) 21222
(vi) 9106
Solution.
(i) Since Ending digit = 4 and 42 = 16
∴ (1234)2 will have 6 as the one’s digit.
(ii) Since Ending digit is 7 and 72 = 49
∴ (26387)2 will have 9 as the one’s digit.
(iii) Since Ending digit is 8, and 82 = 64
∴ (52692)2 will end in 4.
(iv) Since Ending digit is 0.
∴ (99880)2 will end in 0.
(v) Since Ending digit = 2 and 22 = 4
∴ Ending digit of (21222)2 is 4.
(vi) ∵ 62 = 36
∴ Ending digit of (9106)2 is 6.
Property 3. A square number can only have even number of zeros at the end.
Property 4. The squares of odd numbers are odd and the squares of even numbers are even.
Q.7. The square of which of the following numbers would be an odd number/an even number? Why?
(i) 727
(ii) 158
(iii) 269
(iv) 1980
Solution.
(i) 727
Since 727 is an odd number.
∴ Its square is also an odd number.
(ii) 158
Since 158 is an even number.
∴ Its square is also an even number.
(iii) 269
Since 269 is an odd number.
∴ Its square is also an odd number.
(iv) 1980
Since 1980 is an even number.
∴ Its square is also an even number.
Q.8. What will be the number of zeros in the square of the following numbers?
(i) 60
(ii) 400
Solution.
(i) In 60, the number of zero is 1.
∴ Its square will have 2 zeros.
(ii) Since there are 2 zeroes in 400.
∴ Its square will have 4 zeros.
Property 5. The difference between the squares of two consecutive natural numbers is equal to the sum of the two numbers.
Property 6. There are 2n non-perfect square numbers between the squares of the numbers n and n + 1.
Q.9. How many natural numbers lie between 92 and 102? Between 112 and 122?
Solution.
(a) Between 92 and 102
Here, n = 9 and n + 1 = 10
∴ Natural number between 92 and 102 are (2 * n) or 2 * 9, i.e. 18.
(b) Between 112 and 122
Here, n = 11 and n + 1 = 12
∴ Natural numbers between 112 and 122 are (2 * n) or 2 *11, i.e. 22.
Q.10. How many non-square numbers lie between the following pairs of numbers:
(i) 1002 and 1012
(ii) 902 and 912
(iii) 10002 and 10012
Solution.
(i) Between 1002 and 1012
Here, n = 100
∴ n * 2 = 100 * 2 = 200
∴ 200 non-square numbers lie between 1002 and 1012.
(ii) Between 902 and 912
Here, n = 90
∴ 2 * n = 2 * 90 or 180
∴ 180 non-square numbers lie between 90 and 91.
(iii) Between 10002 and 10012
Here, n = 1000
∴ 2 * n = 2 * 1000 or 2000
∴ 2000 non-square numbers lie between 10002 and 10012.
Property 7. The sum of first n odd natural numbers is n2.
OR
If there is a square number, it has to be the sum of the successive odd numbers starting from 1.
Q.11. Find whether each of the following numbers is a perfect square or not?
(i) 121
(ii) 55
(iii) 81
(iv) 49
(v) 69
Solution. Remember: If a natural number cannot be expressed as a sum of successive odd natural numbers starting from 1, then it is not a perfect square.
(i) 121
Since,
121 – 1 = 120
120 – 3 = 117
117 – 5 = 112
112 – 7 = 105
105 – 9 = 96
96 – 11 = 85
85 – 13 = 72
72 – 15 = 57
57 – 17 = 40
40 – 19 = 21
21 – 21 = 0
i.e. 121 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21. Thus, 121 is a perfect square.
(ii) 55
Since,
55 – 1 = 54
54 – 3 = 51
51 – 5 = 46
46 – 7 = 39
39 – 9 = 30
30 – 11 = 19
19 – 13 = 6
6 – 15 = –9
Since, 55 cannot be expressed as the sum of successive odd numbers starting from 1. Thus, 55 is not a perfect square.
(iii) 81
Since,
81 – 1 = 80
80 – 3 = 77
77 – 5 = 72
72 – 7 = 65
65 – 9 = 56
56 – 11 = 45
45 – 13 = 32
32 – 15 = 17
17 – 17 = 0
∴ 81 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17. Thus, 81 is a perfect square.
(iv) 49
Since,
49 – 1 = 48
48 – 3 = 45
45 – 5 = 40
40 – 7 = 33
33 – 9 = 24
24 – 11 = 13
13 – 13 = 0
∴ 49 = 1 + 3 + 5 + 7 + 9 + 11 + 13. Thus, 49 is a perfect square.
(v) 69
Since,
69 – 1 = 68
68 – 3 = 65
65 – 5 = 60
60 – 7 = 53
53 – 9 = 44
44 – 11 = 33
33 – 13 = 20
20 – 15 = 5
5 – 17 = –12
∴ 69 cannot be expressed as the sum of consecutive odd numbers starting from 1. Thus, 69 is not a perfect square.
Property 8. The square of an odd number can be expressed as the sum of two consecutive natural numbers.
Try These
Q1. Express the following as the sum of two consecutive integers.
(i) 212
(ii) 132
(iii) 112
(iv) 192
Solution:
(i) n = 21
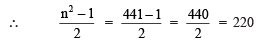
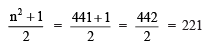
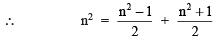
or 212 = 220 + 221 = 441
(ii) n = 13
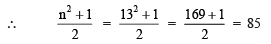

∴ 132 = 85 + 84 = 169
Similarly,
(iii) 112 = 60 + 61 = 121
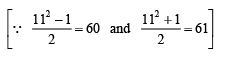
(iv) 192 = 180 + 181 = 361
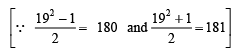
Q2. Do you think the reverse is also true, i.e. is the sum of any two consecutive positive integers is perfect square of a number? Give example to support your answer.
Solution: No, it is not always true.
Example:
(i) 5 + 6 = 11, 11 is not a perfect square.
(ii) 21 + 22 = 43, 43 is not a perfect square.
Property 10. The difference between the squares of two consecutive natural numbers is equal to the sum of the two numbers.
Examples:
92 – 82 = 81 – 64 = 17 = 9 + 8
102 – 92 = 100 – 81 = 19 = 10 + 9
152 – 142 = 225 – 196 = 29 = 15 + 14
1012 – 1002 = 10201 – 10000 = 201 = 101 + 100
Property 11. If (n + 1) and (n – 1) are two consecutive even or odd natural numbers, then (n + 1) X (n – 1) = n2 – 1.
Example:
10 * 12 = (11 – 1) * (11 + 1) = 112 – 1
11 * 13 = (12 – 1) * (12 + 1) = 122 – 1
25 * 27 = (26 – 1) * (26 + 1) = 262 – 1
Q3. Write the square, making use of the above pattern.
(i) 1111112
(ii) 11111112
Solution: Using above pattern we can write:
(i) (111111)2 = 12345654321
(ii) (1111111)2 = 1234567654321
Q4. Can you find the square of the following numbers using the above pattern?
(i) 66666672
(ii) 666666672
Solution: Using the above pattern, we can have:
(i) 66666672 = 44444448888889
(ii) 666666672 = 4444444488888889
Exercise 6.1
Q1. What will be the unit digit of the squares of the following numbers?
(i) 81
(ii) 272
(iii) 799
(iv) 3853
(v) 1234
(vi) 26387
(vii) 52698
(viii) 99880
(ix) 12796
(x) 55555
Solution:
(i) Since, 1 * 1 = 1
∴ The unit’s digit of (81)2 will be 1.
(ii) Since, 2 * 2 = 4
∴ The unit’s digits of (272)2 will be 4.
(iii) Since, 9 * 9 = 81
∴ The unit’s digit of (799)2 will be 1.
(iv) Since, 3 * 3 = 9
∴ The unit’s digit of (3853)2 will be 9.
(v) Since, 4 * 4 = 16
∴ The unit’s digit of (1234)2 will be 6.
(vi) Since 7 * 7 = 49
∴ The unit’s digit of (26387)2 will be 9.
(vii) Since, 8 * 8 = 64
∴ The unit’s digit of (52698)2 will be 4.
(viii) Since 0 * 0 = 0
∴ The unit’s digit of (99880)2 will be 0.
(ix) Since 6 * 6 = 36
∴ The unit’s digit of (12796)2 will be 6.
(x) Since, 5 * 5 = 25
∴ The unit’s digit of (55555)2 will be 5.
Q2. The following numbers are obviously not perfect squares. Give reason.
(i) 1057
(ii) 23453
(iii) 7928
(iv) 222222
(v) 64000
(vi) 89722
(vii) 222000
(viii) 505050
Solution:
(i) 1057
Since, the ending digit is 7 (which is not one of 0, 1, 4, 5, 6 or 9)
∴ 1057 is not a perfect square.
(ii) 23453
Since, the ending digit is 7 (which is not one of 0, 1, 4, 5, 6 or 9).
∴ 23453 is not a perfect square.
(iii) 7928
Since, the ending digit is 8 (which is not one of 0, 1, 4, 5, 6 or 9).
∴ 7928 is not a perfect square.
(iv) 222222
Since, the ending digit is 2 (which is not one of 0, 1, 4, 5, 6 or 9).
∴ 222222 is not a perfect square.
(v) 64000
Since the number of zeros is odd.
∴ 64000 is not a perfect square.
(vi) 89722
Since, the ending digits is 2 (which is not one of 0, 1, 4, 5, 6 or 9).
∴ 89722 is not a perfect square.
(viii) 222000
Since the number of zeros is odd.
∴ 222000 is not a perfect square.
(viii) 505050
The unit’s digit is odd zero.
∴ 505050 can not be a perfect square.
Q3. The squares of which of the following would be odd numbers?
(i) 431
(ii) 2826
(iii) 7779
(iv) 82004
Solution: Since the square of an odd natural number is odd and that of an even number is an even number.
(i) The square of 431 is an odd number.
[∵ 431 is an odd number.]
(ii) The square of 2826 is an even number.
[∵ 2826 is an even number.]
(iii) The square of 7779 is an odd number.
[∵ 7779 is an odd number.]
(iv) The square of 82004 is an even number.
[∵ 82004 is an even number.]
Q4. Observe the following pattern and find the missing digits.
112 = 121
1012 = 10201
10012 = 1002001
1000012 = 1 … 2 …1
100000012 = …
Solution: Observing the above pattern, we have:
(i) (100001)2 = 10000200001
(ii) (10000001)2 = 100000020000001
Q5. Observe the following pattern and supply the missing number.
112 = 121
1012 = 10201
101012 = 102030201
10101012 = ………….
………….2 = 10203040504030201
Solution: Observing the above, we have:
(i) (1010101)2 = 1020304030201
(ii) 10203040504030201 = (101010101)2
Q6. Using the given pattern, find the missing numbers.
12 + 22 + 22 = 32
22 + 32 + 62 = 72
32 + 42 + 122 = 132
42 + 52 + __2 = 212
52 + __2 + 302 = 312
62 + 72 + __2 = __2
Note: To find pattern:
Third number is related to first and second number. How?
Fourth number is related to third number. How?
Solution: The missing numbers are:
(i) 42 + 52 + 202 = 212
(ii) 52 + 62 + 302 = 312
(iii) 62 + 72 + 422 = 432
Q7. Without adding, find the sum.
(i) 1 + 3 + 5 + 7 + 9
(ii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19
(iii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23
Solution:
(i) The sum of first 5 odd numbers = 52 = 25
(ii) The sum of first 10 odd numbers = 102 = 100
(iii) The sum of first 12 odd numbers = 122 = 144
Q8. (i) Express 49 as the sum of 7 odd numbers.
(ii) Express 121 as the sum of 11 odd numbers.
Solution:
(i) 49 =72 = Sum of first 7 odd numbers
= 1 + 3 + 5 + 7 + 9 + 11 + 13
(ii) 121 = 112 = Sum of first 11 odd numbers
= 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21
Q9. How many numbers lie between squares of the following numbers?
(i) 12 and 13
(ii) 25 and 26
(iii) 99 and 100
Solution: Since between n2 and (n + 1)2, there are 2n non-square numbers.
(i) Between 122 and 132, there are 2 *12, i.e. 24 numbers.
(ii) Between 252 and 262, there are 2 * 25, i.e. 50 numbers.
(iii) Between 992 and 1002, there are 2 * 99, i.e. 198 numbers.
Finding the Square of a number
Example. Find the square of 27.
Solution: (27)2 = (20 + 7)2
Using the formula (a + b)2 = a2 + 2ab + b2, we have
(20 + 7)2 = (20)2 + 2 * (20) * (7) + (7)2
= 400 + 280 + 49
= 729
Thus, (27)2 = 729
Note: For any number ending with 5, the square is a(a + 1) hundred + 25.
For example,
(25)2 = 2(2 + 1) * 100 + 25 = 625
(35)2 = 3(3 + 1) * 100 + 25 = 1225
(65)2 = 6(6 + 1) *100 + 25 = 4225
(125)2 = 12(12 + 1) * 100 + 25 = 15625
Pythagorean Triplets
If three numbers a, b and c are such that a2 + b2 = c2, then they are called Pythagorean Triplets and they represent the sides of a right triangle.
Example:
(i) 3, 4, 5 form a Pythagorean triplet.
[∵ 32 + 42 = 52]
(ii) 8, 15, 17 form a Pythagorean triplet.
[∵ 82 + 152 = 172]
Note: For any natural number n, (n > 1), we have
(2n)2 + (n2 – 1)2 = (n2 + 1)2
such that 2n, n2 – 1 and n2 + 1 are a Pythagorean triplet.
Example. Write a Pythagorean triplet whose one member is 15.
Solution: Since, a Pythagorean triplet is given by 2n, n2 – 1 and n2 + 1.
∴ 2n = 15 or n = 15/2 is not an integer.
So, let us assume that
n2 – 1 = 15
or n2 = 15 + 1 = 16
or n2 = 42, i.e. n = 4
Now, the required Pythagorean triplet is
2n, n2 – 1 and n2 + 1
or 2(4), 42 – 1 and 42 + 1
or 8, 15 and 17
Remember
All Pythagorean triplets may not be obtained using the above form.
Question: Find the square of the following numbers containing 5 in unit’s place.
(i) 15 (ii) 95 (iii) 105 (iv) 205
Solution:
(i) (15)2 = 1 * (1 + 1) * 100 + 25
= 1 * 2 * 100 + 25
= 200 + 25 = 225
(ii) (95)2 = 9(9 + 1) * 100 + 25
= 9 * 10 * 100 + 25
= 9000 + 25 = 9025
(iii) (105)2 = 10 * (10 + 1) * 100 + 25
= 10 *11 * 100 + 25
= 11000 + 25 = 11025
(iv) (205)2 = 20 * (20 + 1) * 100 = 25
= 20 * 21 * 100 + 25
= 42000 + 25 = 42025
Exercise 6.2
Que 1. Find the square of the following numbers.
(i) 32 (ii) 35 (iii) 86 (iv) 93 (v) 71 (vi) 46
Solution:
(i) (32)2 = (30 + 2)2
= 302 + 2(30)(2) + (2)2
= 900 + 120 + 4 = 1024
(ii) (35)2 = (30 + 5)2
= (30)2 + 2(30)(5) + (5)2
= 900 + 300 + 25
= 1200 + 25 = 1225
Second method
352 = 3 * (3 + 1) * 100 + 25
= 3 * 4 * 100 + 25
= 1200 + 25 = 1225
(iii) (86)2 = (80 + 6)2
= (80)2 + 2(80)(6) + (6)2
= 6400 + 960 + 36 = 7396
(iv) (93)2 = (90 + 3)2
= (90)2 + 2(90)(3) + (3)2
= 8100 + 540 + 9 = 8649
(v) (71)2 = (70 + 1)2
= (70)2 + 2(70)(1) + (1)2
= 4900 + 140 + 1 = 5041
(vi) (46)2 = (40 + 6)2
= (40)2 + 2(40)(6) + (6)2
= 1600 + 480 + 36 = 2116
Que 2. Write a Pythagorean triplet whose one member is
(i) 6 (ii) 14 (iii) 16 (iv) 18
Solution:
(i) Let 2n = 6 ∴n = 3
Now, n2 – 1 = 32 – 1 = 8
and n2 + 1 = 32 + 1 = 10
Thus, the required Pythagorean triplet is 6, 8, 10.
(ii) Let 2n = 14 ∴ n = 7
Now, n2 – 1 = 72 – 1 = 48
and n2 + 1 = 72 + 1 = 50
Thus, the required Pythagorean triplet is 14, 48, 50.
(iii) Let 2n = 16 ∴n = 8
Now, n2 – 1 = 82 – 1
= 64 – 1 = 63
and n2 + 1 = 82 + 1
= 64 + 1 = 65
Thus, the required Pythagorean triplet is 16, 63, 65.
(iv) Let 2n = 18 ∴n = 9
Now, n2 – 1 = 92 – 1
= 81 – 1 = 80
and n2 + 1 = 92 + 1
= 81 + 1 = 82
Thus, the required Pythagorean triple is 18, 80, 82.
Q. Write all the square numbers between 100 and 300. Ans: 121, 144, 169, 196, 225, 256 and 289 Q. Write all the non-square numbers between 42 and 52. Ans: 17, 18, 19, 20, 21, 22, 23 and 24 Q. Fill in the blanks: Ans: (i) 11 (ii) 11 + 13 Q. Fill in the blanks: Q. Find the square of the following numbers actual multiplication: Ans: (i) 1521 (ii) 1764 Q. Write the Pythagorean triplet whose smallest number is 8. Ans: 8, 15, 17 Q. Find a Pythagorean triplet in which one member is 12. Ans: 12, 35, 37 |
Square Roots
Finding the square root of a number is just the opposite operation of squaring it. For example, the square of 5 is 25.
∴ Square root of 25 is 5.
Note: We kwon that (–2) * (–2) = 4, then we say that (–2) is also the square root of 4. Similarly, square roots of 100 are 10 and (–10).
But in this chapter, we shall be studying about positive square roots only
Finding Square Root Through Prime Factorisation
We know that a factor that occurs once in the prime factorisation of a number, occurs twice in the prime factorisation of its square. Thus, we can use this fact of prime factorisation of a number to find the square root of a perfect square.
Note: A perfect square has complete pairs of its prime factors.
Example. Is 1008 a perfect square? If not, find the smallest multiply of 1008 which is a perfect square end then find the square root of the new number.
Solution: We have
1008 = 2 * 2 * 2 * 2 * 3 * 3 * 7
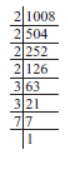
As the prime factor 7 has no pair.
∴1008 is not a perfect square. Obviously, if 7 gets a pair, then the number will become a perfect square.
∴1008 * 7 = [2 * 2 * 2 * 2 * 3 * 3 * 7] * 7
or 7056 = 2 * 2 * 2 * 2 * 3 * 3 * 7
Thus, 7056 is the required multiple of 1008 which is a perfect square.
Now,  = 2 * 2 * 3 * 7 = 84
= 2 * 2 * 3 * 7 = 84
Question: (i) 112 = 121. What is the square root of 121?
(ii) 142 = 196. What is the square root of 196?
Solution: (i) The square root of 121 is 11.
(ii) The square root of 196 is 14.
Think, Discuss and Write
Question:
(–1)2 = 1. Is –1, a square root of 1?
(–2)2 = 4. Is –2, a square root of 4?
(–9)2 = 81. Is –9, a square root of 81?
Solution:
(i) Since (–1) * (–1) = 1
i.e. (–1)2 = 1
∴ Square root of 1 can also be –1.
Similarly,
(ii) Yes (–2) is a square root of 4.
(iii) Yes (–9) is a square root of 81.
Since, we have to consider the positive square roots only and the symbol for a positive square
root is √
∴ 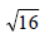 = 4 [and not (–4)]
= 4 [and not (–4)]
Similarly, 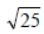 means, the positive square root of 25, i.e. 5.
means, the positive square root of 25, i.e. 5.
Note: We can also find the square root by subtracting successive odd numbers starting from 1.
Question: By repeated subtraction of odd numbers starting from 1, find whether the following numbers are perfect squares or not? If the number is a perfect square, then find its square root.
(i) 121 (ii) 55 (iii) 36 (iv) 49 (v) 90
Solution:
(i) Subtracting the successive odd numbers from 121, we have
121 – 1 = 120 120 – 3 = 117
117 – 5 = 112 112 – 7 = 105
105 – 9 = 96 96 – 11 = 85
85 – 13 = 72 72 – 15 = 57
57 – 17 = 40 40 – 19 = 21
21 – 21 = 0
∴ 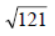 = 11. [∵ We had to subtract the first 11 odd numbers.]
= 11. [∵ We had to subtract the first 11 odd numbers.]
(ii)
∵ 55 – 1 = 54 54 – 3 = 51
51 – 5 = 46 46 – 7 = 39
39 – 9 = 30 30 – 11 = 19
19 – 13 = 6 6 – 15 = –9
and we do not reach to 0. ∴ 55 is not a perfect square.
(iii)
∵ 36 – 1 = 35 35 – 3 = 32
32 – 5 = 27 27 – 7 = 20
20 – 9 = 11 11 – 11 = 0
and we have obtained 0 after subtracting 6 successive odd numbers.
∴ 36 is a perfect square.
Thus, 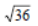 = 6.
= 6.
(iv) We have
49 – 1 = 48 48 – 3 = 45
45 – 5 = 40 40 – 7 = 33
33 – 9 = 24 24 – 11 = 13
13 – 13 = 0
∵ We have obtained 0 after successive subtraction of 7 odd numbers.
∴ 49 is a perfect square,
Thus, 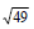 = 7.
= 7.
(v) We have:
90 – 1 = 89 89 – 3 = 86
86 – 5 = 81 81 – 7 = 74
74 – 9 = 65 65 – 11 = 54
54 – 13 = 41 41 – 15 = 26
26 – 17 = 9 9 – 19 = –10
Since, we can not reach to 0 after subtracting successive odd numbers.
∴ 90 is not a perfect square.
|
276 docs|155 tests
|
FAQs on NCERT Solutions for Class 8 Maths - Squares and Square Roots- 1
| 1. What is Exercise 6.1 about? |  |
| 2. What are Pythagorean Triplets? |  |
| 3. What does Exercise 6.2 cover? |  |
| 4. What is the purpose of the article "Think, Discuss and Write" in relation to Squares & Square Roots? |  |
| 5. What are some NCERT Solutions provided for Squares & Square Roots-1? |  |
















