Ratio and Proportion Class 6 Notes Maths Chapter 12
| Table of contents |

|
| Introduction |

|
| Ratio |

|
| Proportion |

|
| Unitary Method |

|
Introduction
In daily life, we often compare quantities to understand how they relate to each other. There are two main ways to compare quantities:
- Difference Comparison:This method involves finding the difference between two quantities. For example, if you have 10 apples and your friend has 15 apples, you can find out how many more apples your friend has by subtracting: 15 - 10 = 5 apples. This tells you the exact amount by which one quantity is greater or smaller than the other.
- Ratio Comparison:This method involves using division to find out how many times one quantity is compared to another. For example, if a toy costs ₹200 and a book costs ₹50, you can compare their costs by dividing: ₹200 ÷ ₹50 = 4. This tells you that the toy costs 4 times more than the book.

Ratio
A ratio is a way to compare two quantities to see how many times one quantity is relative to another. It is denoted by the symbol ":" and shows the relationship between the quantities.
Example: Anna weighs 30 kg, and her brother weighs 90 kg.
Ratio of Anna’s weight to her brother’s weight:
Convert the weights into the same unit (kg).
Ratio = 90 kg : 30 kg = 90 ÷ 30 = 3 : 1
This means Anna’s brother weighs 3 times more than Anna.
Same Unit
To compare two quantities using ratios, they must be expressed in the same unit. If the quantities are in different units, you need to convert them to the same unit before calculating the ratio. This ensures an accurate comparison.
Example 1: A bottle contains 500 ml of juice, and a jug contains 3 liters of juice.
Ans: Convert the jug’s volume to ml:
3 liters = 3000 ml.
Ratio of the jug’s volume to the bottle’s volume:
Ratio = 3000 ml : 500 ml = 3000 ÷ 500 = 6 : 1
This means the jug holds 6 times more juice than the bottle.
Example 2: A bike travels 8 kilometers, and a car travels 5000 meters.
Initial Ratio: 8 kilometers : 5000 meters
To compare these, convert kilometers to meters:
1 kilometer = 1000 meters
8 kilometers = 8 × 1000 = 8000 meters
Now, the ratio is:
8000 meters : 5000 meters
Simplify this ratio:
8000 ÷ 5000 = 1.6
5000 ÷ 5000 = 1
Simplified Ratio: 1.6:1 or 8:5 (by multiplying both terms by 5)
The bike travels 1.6 times as far as the car.
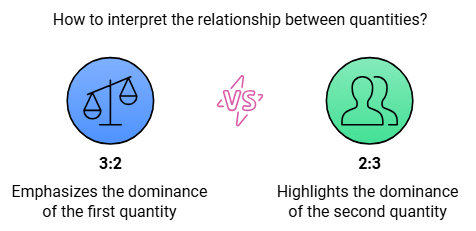
Order Matters
The order in which quantities are compared matters. For example, 3:2 is different from 2:3.
The order determines which quantity is being compared to which, leading to different interpretations of the relationship between them.
Example: Comparing Apples and Oranges
Scenario 1: A basket contains 3 apples and 2 oranges.
Ratio of apples to oranges: 3:2
Interpretation: There are 3 apples for every 2 oranges.
Scenario 2: Another basket contains 2 apples and 3 oranges.
Ratio of apples to oranges: 2:3
Interpretation: There are 2 apples for every 3 oranges.
In this case:
3:2 means the basket has more apples relative to oranges.
2:3 means the basket has more oranges relative to apples.
Lowest Form
Just like fractions, ratios can be simplified to their lowest form. Simplifying a ratio means reducing it so that the numbers are as small as possible while still maintaining the same relationship between the quantities. This makes the ratio easier to understand and compare.
Example 1: A recipe requires 50 grams of sugar for every 15 grams of flour.
Initial Ratio: 50:15
To simplify this ratio:
Find the Greatest Common Divisor (GCD): The GCD of 50 and 15 is 5.
Divide both terms of the ratio by the GCD:
50 ÷ 5 = 10
15 ÷ 5 = 3
Simplified Ratio: 10:3
The simplified ratio 10:3 means that for every 10 grams of sugar, there are 3 grams of flour.
Example 2: There are 18 boys and 12 girls in a club.
Initial Ratio: 18:12
To simplify this ratio:
Find the Greatest Common Divisor (GCD): The GCD of 18 and 12 is 6.
Divide both terms of the ratio by the GCD:
18 ÷ 6 = 3
12 ÷ 6 = 2
Simplified Ratio: 3:2
The simplified ratio 3:2 means there are 3 boys for every 2 girls in the club.
Equivalent Ratios
Two ratios are considered equivalent if they represent the same relationship between the quantities, even though the numbers in the ratios may be different. This means that when you simplify each ratio to its lowest form, they should be the same. Equivalent ratios are like fractions that are equal to each other.
We can get equivalent ratios by multiplying or dividing the numerator and denominator by the same number.
Example 1: Compare the ratios 6:4 and 3:2.
Ans: To check if they are equivalent:
Simplify 6:4: Divide both terms by their Greatest Common Divisor (GCD), which is 2.
6 ÷ 2 = 3
4 ÷ 2 = 2
Simplified Ratio: 3:2
Compare with 3:2: Since both ratios simplify to 3:2, they are equivalent.
Interpretation: 6:4 and 3:2 are equivalent ratios.
Example 2: Find the equivalent ratios of 2:5.
Ans: To find equivalent ratios, you can multiply both terms by the same number:
Multiply by 2:
2 × 2 = 4
5 × 2 = 10
Equivalent Ratio: 4:10
Multiply by 3:
2 × 3 = 6
5 × 3 = 15
Equivalent Ratio: 6:15
Interpretation: 4:10 and 6:15 are equivalent to 2:5.
Example 3: A recipe calls for 4 cups of flour to 2 cups of sugar (4:2). If you scale up the recipe and use 8 cups of flour, how much sugar is needed to maintain the same ratio?
Ans: Find the Scaling Factor: Multiply the ratio 4:2 by 2 to get the new amounts.
4 × 2 = 8 cups of flour
2 × 2 = 4 cups of sugar
To maintain the ratio 4:2, you need 4 cups of sugar when using 8 cups of flour.
Uses of Ratios
- Ratios are used in various real-life situations such as comparing prices, lengths, or any quantities where division makes sense.
- Ratios are also used in proportion, which involves comparing two ratios to determine equality.
Proportion
A proportion is an equation that shows that two ratios are equal. It means that the ratios on either side of the equation are equivalent.
When two ratios are compared and found to be equal, we say they are in proportion. This can be expressed using the symbol "::" or "=".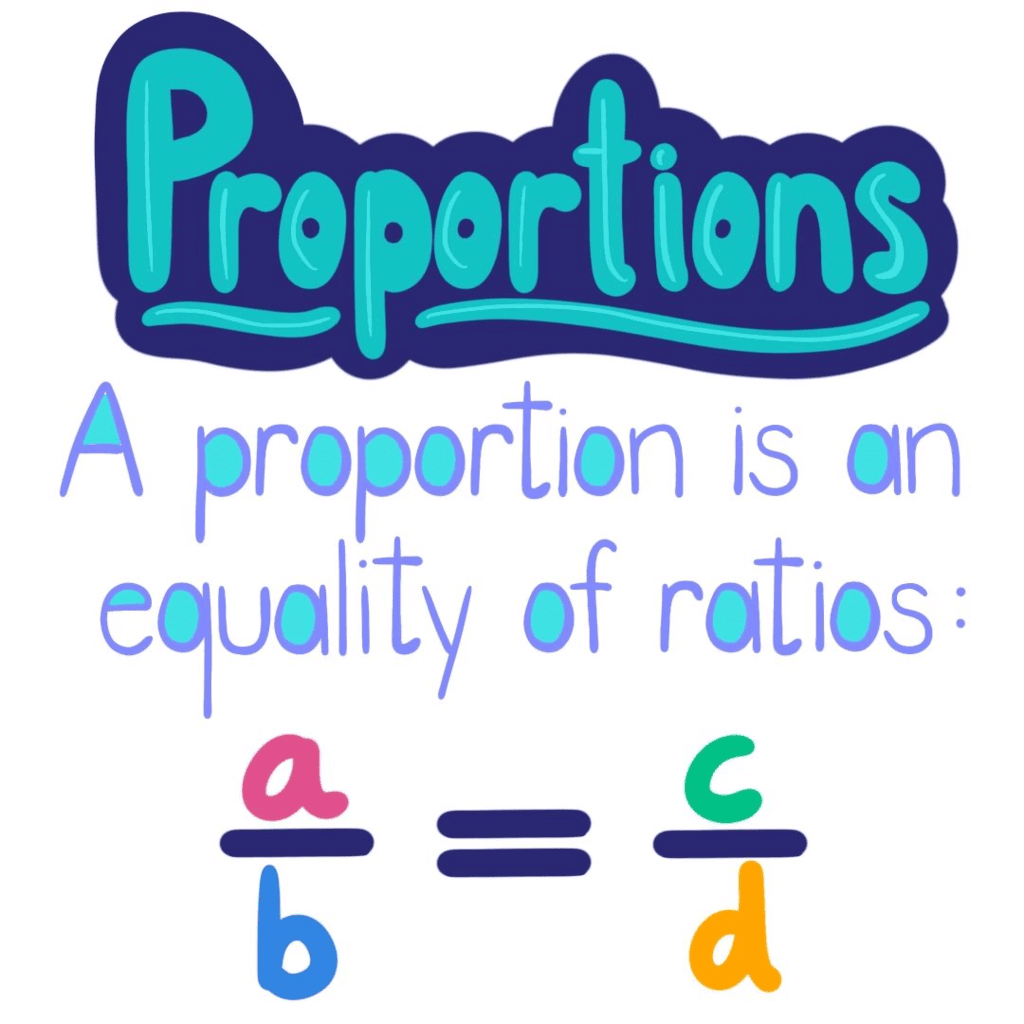
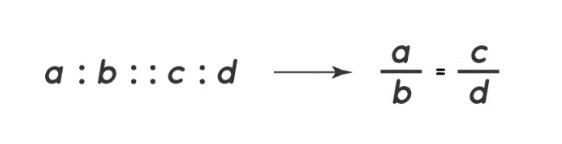
Example: If 2 kg of apples cost ₹60, and 4 kg of apples cost ₹120, then the two ratios are 2:60 and 4:120.
Simplifying these, 2:60 = 1:30 and 4:120 = 1:30. Since the ratios are equal, 2:60 and 4:120 are in proportion.
This can be written as:
2:60::4:120
This is read as "2 is to 60 as 4 is to 120."
Proportions are often used to solve problems where you need to find an unknown quantity when the relationship between quantities is known.
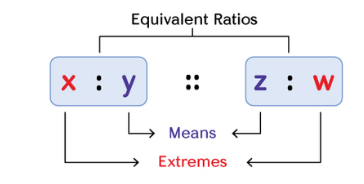
Terms in a Proportion
In a statement of proportion, there are four quantities involved, which are taken in a specific order.
- First and Fourth Terms: These are known as the extreme terms.
- Second and Third Terms: These are called the middle terms.
For example, in the proportion a:b::c:d,
a and 𝑑 are the extreme terms, and
𝑏 and 𝑐 are the middle terms.
Importance of Units
For quantities to be compared in a proportion, they must be in the same units. If not, they must first be converted to the same unit before checking for proportion.Proportional Relationships
Proportions are used to maintain equality in comparisons, such as dividing profits according to investment ratios or comparing the cost of goods based on quantity.
Example: Are 20, 40, 60, 120 in proportion?
Ans: First we will find 20:40 and 60:120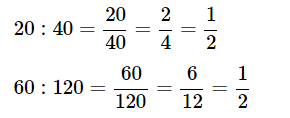
The numbers in the simplest form are equal.
Yes, 20, 40, 60, 120 are in proportion.
Unitary Method
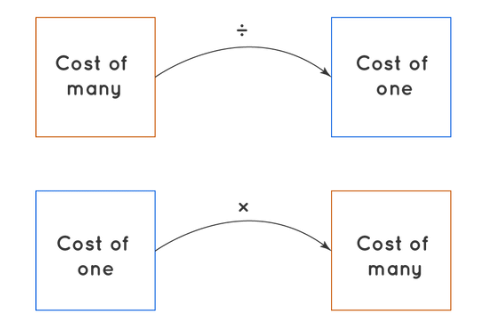
The unitary method is a technique used to find the value of a single unit and then use it to determine the value of multiple units. This method is useful when you need to solve problems involving ratios, rates, or proportions.
- Find the Value of One Unit: First, determine the value of one unit from the given information.
- Find the Value of Multiple Units: Use the value of one unit to find the value for the required number of units.
Example 1: Reshma purchased 2 notebooks for ` 24. What is the price of one notebook?
Ans:
Find the Value of One Unit: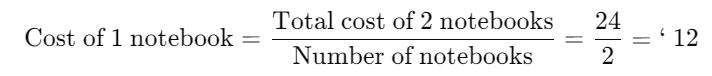
Find the Cost of 5 Notebooks:
So, the cost of 5 notebooks is ` 60.
Example 2:A scooter requires 2 litres of petrol to cover 80 km. How many litres of petrol are needed to cover 1 km?
Ans: Find the Petrol Required for 1 km: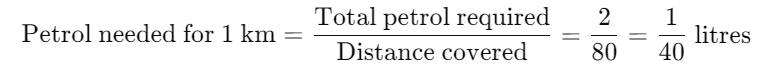
Find Petrol Required to Cover 120 km: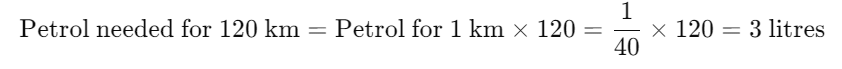
So, 3 litres of petrol are needed to cover 120 km.
FAQs on Ratio and Proportion Class 6 Notes Maths Chapter 12
| 1. What is the definition of a ratio? |  |
| 2. How do you simplify a ratio? |  |
| 3. What is a proportion, and how is it different from a ratio? |  |
| 4. How can the unitary method be applied to solve problems involving ratios and proportions? |  |
| 5. What are some real-life applications of ratios and proportions? |  |
















