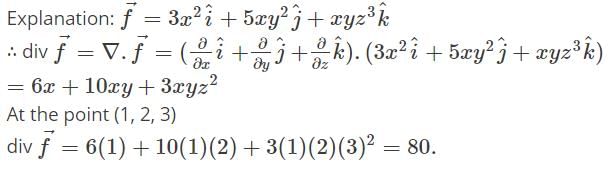Divergence & Curl of a Vector Field | Electromagnetic Fields Theory (EMFT) - Electrical Engineering (EE) PDF Download
| Table of contents |

|
| Introduction |

|
| Divergence and Curl of a Vector Field |

|
| Divergence Theorem |

|
| Curl of a Vector Field |

|
| Solved Examples |

|
| Practice Questions |

|
Introduction
- We had defined divergence of a vector field and had obtained an expression for the divergence in the Cartesian coordinates. We also derived the divergence theorem which connects the flux of a vector field with the volume integral of the divergence of the field.
- Physically, the divergence, as the name suggests is a measure of the amount of spread that the field has at a point.
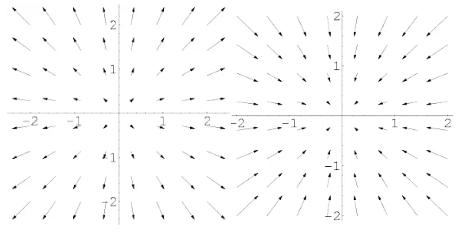
- For instance, in the figure above, the vector field shown to the left has a positive divergence while that to the right has a negative divergence. In electrostatics, we will see that the field produced by a positive charge has positive divergence while a negative charge produces an electrostatic field with negative divergence.
Divergence and Curl of a Vector Field
- Divergence, curl were extensively used in fluid dynamics from which a lot of nomenclatures have arisen. Let us consider a fluid flowing through an elemental volume of dimension
with its sides oriented parallel to the Cartesian axes.
- In the figure below, we show only the y-component of the velocity of the fluid entering and leaving the elemental volume. Let the density of the fluid at
and the y-component of the velocity be vy. We define a vector
The mass of the fluid flowing into the volume per unit time through the left face which has an outward normal
is given by:
- Mass of the fluid flowing out is
Retaining only the first order term in a Taylor series expansion, we have
- Thus the net increase in mass is
This is the increase due to the y-component of the velocity. We can write similar expressions for the flow in the x and z directions. The net increase in mass per unit time is
where we have put the volume element
so as not to confuse with the vector
defined above.
- Another of of talking about the net increase in mass is to realize that since the volume is fixed, the increase in mass is due to a change in the density alone. Thus the rate of increase of mass is
- Equating these two expressions, we get what is known as the equation of continuity in fluid dynamics,
- To see what this equation implies, consider, for example a vector field given by
The field has been plotted using Mathematica (see figure)
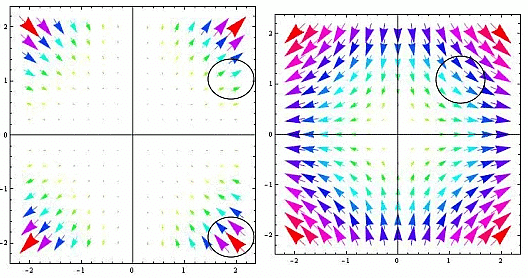
- To the left is plotted
Note that in the first and the third quadrants the divergence is positive while in the other two quadrants it is negative. The figure to the right is for the force field
which has zero divergence.
- The size of the arrow roughly represents the magnitude of the vector. The divergence is given by 4xy. In the first and the third quadrants (x,y both positive or both negative) divergence is positive.
- One can see that in these quadrants, if you take any closed region the size of the arrows which are entering the region are smaller than those leaving it. Thus the density decreases, divergence is positive. Reverse is true in the even quadrants.
- In the figure to the right, the force field
has zero divergence. If you take a closed region in this figure, you find as many vectors are getting in as are going out. The field is a solenoidal (zero divergence) field.
Divergence Theorem
- Recall divergence theorem
where the surface integral is taken over a closed surface defining the enclosed volume. As an example consider the surface integral of the position
over the surface of a cylinder of radius a and height h.
- Evaluating the surface integral by use of the divergence theorem is fairly simple. Divergence of position vector has a value 3 because
Thus the volum integral of the divergence is simply three times the volume of the cylinder which gives
- Direct calculation of the surface integral can be done as follows. For convenience, let the base of the cylinder be in the x-y plane with its centre at the origin.
- There are three surface of the cylinder, a top cap, a bottom cap and the curved surface. For the top cap, the normal vector
direction, so that
On the top surface z is constant and is given by z=h. Thus
For the bottom cap
direction so that
- However, the value of z on this surface being zero, the flux vanishes. We are now left with the curved surface for which the outward normal is parallel to the x-y plane. The unit vector on this surface is
However, on the surface
- Thus the surface integral is
Adding to this the contribution from the top and the bottom face, the surface integral works out to
as was obtained from the divergence theorem
- As a second example, consider a rather nasty looking vector field
over the surface of a cubical box
We will not attempt to calculate the surface integral directly.
- However, the divergence theorem gives a helping hand.
- We need to calculate the triple integral
As the integrand has no z dependence, the z-integral evaluates to 1. The volume integral is
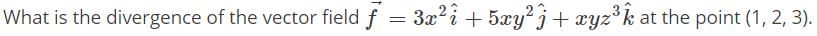
Curl of a Vector Field
- We have seen that the divergence of a vector field is a scalar field. For vector fields it is possible to define an operator which acting on a vector field yields another vector field. The name curl comes from “circulation” which measures how much does a vector field “curls” about a point.
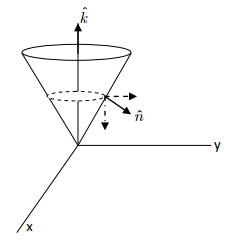
- Consider an open surface of the type shown – something like an inverted pot with a rim. We wish to calculate the surface integral of a vector field defined over this surface.
- Let's divide the surface into many small parts and find the line integral along the edge of each small part. An example of such a small part with its edge is displayed. If we describe the edge of this surface in a counterclockwise direction, the normal to the surface will point outward.
- If we look at each small part individually and compute the line integral along the edge ΔCi of each part, the contributions from neighboring areas will cancel out because the integrals along the edges are in opposite directions (observe the black and red arrows on the edges of two parts).
- After considering all the small parts, we are left with the unbalanced line integral at the boundary. This is shown in the figure below.
- The line integral around the boundary for ABCD is equal to the line integral around the boundary for ABEF because the integration is done along CD in the former and DC in the latter.
- Thus we have,
(1)
- The quantity in the parenthesis in the last expression is defined as the curl of the vector field
limit of the elemental surface goes to zero. Curl being a vector, its direction is specified as the outgoing normal to the surface element.
- It may be noted that because the definition is valid in the limit of the surface area going to zero, it is a point relationship. Using this definition, we can write the previous equation (1) as
- This equation relates the surface integral of the curl of a vector field with the line integral of the vector field and is known as “Stoke’s Theorem”.
Solved Examples
Example.1. Calculate the flux of the vector field over the surface of a unit cube whose edges are parallel to the axes and one of the corners is at the origin. Use this result to illustrate the divergence theorem.
- The geometry of the cube along with the direction of surface normalsare shown in the figure. Consider the base of the cube which is the plane z=0. On this face
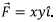
- Since the normal is along the -z direction flux from this face is zero. Similarly, the flux from the other two faces which meet at the origin are also zero. Consider the top face where z=1.
- On this face
The normal is in the +z direction, so that the flux is
Likewise, the flux from the other two faces are also ½ each. The total flux, therefore, is 3/2. The divergence of the field
- The volume integral of the divergence is
- By symmetry, this is 3 times
1/2. Thus the volume integral of the divergence is 3/2.
Example.2. Calculate the flux of the vector field over the surface of a unit sphere. Use this result to illustrate the divergence theorem. (Use spherical coordinates).
- Divergence of the field is
Thus the volume integral of the divergence over the surface of a unit sphere is just
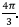
- To calculate the surface integral we note that the normal on the surface of the sphere is along the radial direction and is given by
where R=1 is the radius of the sphere. Thus
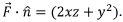
- Since the surface element on the sphere is
we have , substituting (in spherical polar)
- The first term gives zero because of vanishing of the integral over φ. We are left with
Example.3. Calculate the flux of the vector over the surface of a right circular cylinder of radius R bounded by the surfaces z=0 and z=h. Calculate it directly as well as by use of the divergence theorem.
- Let the base of the cylinder be at z=0 and the top at z=h. The origin is at the centre of the base. The cylinder has three surfaces. For the bottom surface, the direction of the normal is along
and on this surface z=0.
- The surface integral for this surface is
For the top surface, the normal is along
the surface integral is
For the curved surface the direction of the normal is outward radial direction in the x-y plane which is
so that the surface integral is
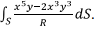
- The integral is done in the cylindrical coordinates by polar substitution
The surface element is
Thus the integral become The angle integral in both cases gives zero. Thus the total flux is only contributed by the top surface and is
The angle integral in both cases gives zero. Thus the total flux is only contributed by the top surface and is
This can also be seen by the divergence theorem.
The volume integral is
Example.4. Calculate the flux of the position vector through a torus of inner radius a and outer radius b. Use the result to illustrate divergence theorem. (* This is a hard problem).
- Geometrically a torus is obtained by taking a circle, say in the x-z plane and rotating it about the z-axis to obtain a solid of revolution. Let us define the mean radius of the torus to be
and the radius of the circle which is being revolved about the z-axis to be
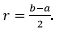
- The position vector of an arbitrary point on the torus is defined as follows:
- Consider the coordinate of an arbitrary point on the circle which is in the x-z plane. Let the position of the point make an angle φ with the x-axis. The coordinate of this point is
When the circle is rotated about the z-axis by an angle θ, the z coordinate does not change.
- However, the x and y coordinates change and become
- Thus an arbitrary point on the torus can be parameterized by
given by the above expressions. A surface element on the torus is then obtained by the area formed by an arc obtained by incrementing
and the arc formed by incrementing
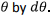
- The area element is therefore given by the cross product
(The unit vector on the surface is directed along the direction of the cross product.). The partial derivatives are given by
- Thus
(the order of the cross product determines the outward normal).
- Thus , substituting
- Since the integrand is independent of θ the integral over it gives 2π. The integral over the remaining angle is straightforward. We can simplify the integrand as follows :
- The second and the third term in the integral vanish, the remaining two terms give
which makes the total contribution to the surface integral as
- However, the problem is straightforward if we apply the divergence theorem. The divergence of the position vector is 3. Thus by divergence theorem, the surface integral is 3 times the volume of the toroid.
- The volume of the toroid is rather easy to calculate if we note that if we cut it along a section, the toroid becomes a cylinder of radius r and length 2πR. Thus the volume of the toroid is
Thus 3 times the volume is
consistent with our direct evaluation of the surface integral.
Example.5. Calculate the flux of the vector field over the surface defined by
- The surface is sketched below. Since
the region of interest is
Notice that the divergence theorem is not directly applicable because the surface is not closed.
- However, one can close the surface by adding a cap to the surface at z=3. We will calculate the flux by applying the divergence theorem to this closed surface and then explicitly subtract the surface integral over the cap.
- The divergence of the field is given by
- Thus the surface integral over the closed surface is thus given by
To evaluate this, consider a disk lying between z and z+dz. The circular disk of width dz has a volume
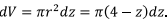
- This gives the surface integral to be 4π. We have to now subtract from this the surface integral over the cap that was added by us, which is directed along
direction. On this surface z=3 so that the radius of the disk is 1. This integral
can be easily calculated and shown to have value zero. Thus the required surface integral has a value 4π.
Practice Questions
In the following questions(Q1-Q5) calculate the flux both by direct integration and also by application of the divergence theorem.
Q.1. Calculate the flux of the field over the surface of a right circular cylinder of radius R and height h in the first octant, i.e. in the region (x>0, y>0, z>0).
- For the curved surface of the cylinder, the unit vector is
which gives
- Parameterize
Since we are confined to the first octant
- The flux through the slant surface is
The top and the bottom caps are in the
the contribution from these two give zero by symmetry. T
- here are two more surfaces if we consider the first octant, they are the positive x-z plane and the positive y-z plane., the normal to the former being in the direction of
that for the latter is along
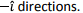
- The flux from the former is
while that from the latter is
- Adding up all the contributions, the total flux from the closed surface is zero. This is consistent with the fact that the divergence of the field is zero.
Q.2. Evaluate the surface integral of the vector field over the surface of a unit cube with the origin being at one of the corners.
- There are six faces. For the face at x=0, since the surface is directed along
the surface integral is
The face at x=1 gives +1/2. The faces at y=0 and that at z=0 gives zero because the field is proportional to y and z respectively.
- The contribution to flux from y=1 is 1 and that from z=1 is 3/2. Adding, the flux is 5/2 units. This can also be done by the divergence theorem. Divergence of the field is 2x+3y, so that the volume integral is
Q.3. Calculate the flux of over the surface of a sphere of radius R with its centre at the origin.
- The divergence of the given vector field is
Thus, by divergence theorem, the flux is
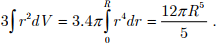
- We can show this result by direct integration. The unit normal on the surface of the sphere is given by
that the flux is
This integral can be conveniently evaluated in a spherical polar coordinates with
The surface element on the sphere is
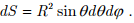
- By symmetry, the flux can be seen to be
. (Note that we decided to do the integral involving z4 rather than x4 or y4 because the azimuthal integral gives 2π in this case. The integral is easy to perform with the substitution
which gives the flux to be
Q.4. Calculate the flux of through the surface defined by a cone
- The divergence of the field is 3. The flux, therefore, is 3 times the volume of the cone which is
The flux is thus π. The direct calculation of the flux involves two surfaces, the slant surface and the cap, as shown in the figure.
- The cap is in the xy plane and has an outward normal
(because on the cap z=1 and the cap is a disk of unit radius). Thus it remains to be shown that the flux from the slanted surface vanishes. At any height z, the section parallel to the cap is a circle of radius z. Since, the height and the radius of the cap are 1 each, the semi angle of the cone is 450.
- Thus the normal to the slanted surface has a component
along the z direction and
in the x-y plane. The component in the xy plane can be parameterized by the azimuthal angle φ and we can write
The area element can be written as
appears because the length element is along the slant.
- Thus the contribution from the slanted surface is
this integral can be evaluated and shown to be zero.
Q.5. Evaluate the flux through an open cone for the field
- This problem is to be attempted similar to the problem 5 of the tutorial, i.e., by closing the cap and subtracting the contribution due to the cap. The divergence being 3, the flux from the closed cone is 3 times the volume of the cone which gives 8π.
- The contribution from the top face (which is a disk of radius 2) is
the net flux is zero. (You can also try to get this result directly as done in problem 4, where we showed that the flux from the curved surface is zero).
|
10 videos|53 docs|56 tests
|
FAQs on Divergence & Curl of a Vector Field - Electromagnetic Fields Theory (EMFT) - Electrical Engineering (EE)
| 1. What is the mathematical definition of divergence of a vector field? |  |
| 2. How is the curl of a vector field defined in mathematics? |  |
| 3. What is the physical interpretation of the divergence of a vector field? |  |
| 4. How can the divergence theorem be used in practical applications? |  |
| 5. Can you provide an example illustrating the calculation of curl of a vector field? |  |