Magnetostatics - 1 | Electromagnetic Fields Theory (EMFT) - Electrical Engineering (EE) PDF Download
What is Magnetostatics?
- Sources of magnetic field are steady currents. In such a field a moving charge experiences a sideways force. Recall that an electric field exerts a force on a charge, irrespective of whether the charge is moving or static.
- Magnetic, field, on the other hand, exerts a force only on charges that are moving. Under the combined action of electric and magnetic fields, a charge experiences, what is known as Lorentz force:
where the fieldknown by various names, such as, “magnetic field of induction”, “magnetic flux density”, or simply, as we will be referring to it in this course as the “magnetic field”.
- Note that the force due to the magnetic field is expressed as a cross product of two vectors, the force is zero when the charges are moving perpendicular to the direction of the magnetic field as well.
Current and Current Density
- Let us look at the definition of current. Current is a scalar quantity which is the amount of charge that crosses the boundary of a surface of a volume per unit time, the surface being oriented normal to the direction of flow.
- In the steady-state there is no accumulation of charge inside a volume through whose surface the charges flow in. This results in the “equation of continuity”.
- If p is the charge density, the current is given by
wherethe current density.
- Recalling that
we get,
- Here, the minus sign is taken because, we define the current to be positive when it flows from outside the volume to the inside and the surface normal, as in the previous lectures, is taken to be outward. Using the divergence theorem, we can rewrite this as
- Since the relationship is true for arbitrary volume, we can equate the integrands from both sides, which results in the equation of continuity :
- The principle is a statement of conservation of electric charge.
- As we stated earlier in the lecture, magnetostatics deals with steady currents which implies
so that for magnetostatic phenomena, we have
Though we will not be talking much about it, we would like to mention that this equation is also relativistically invariant.
Biot- Savart’s Law & Ampere's Law
- Recall that the electric field at a point due to a charge distribution was calculated by the principle of superposition of fields due to charges inside infinitesimal volume elements which make this charge distribution.
- The field due to the infinitesimal charge element is given by Coulomb’s law, which is an inverse square law. We take a similar approach to calculate the magnetic field due to a charge distribution.
- We consider a current distribution to comprise of infinitesimal current elements whose direction is taken along the direction of the current flow. If
is such a current element located at the position
the field due to it at the position
given by the law of Biot and Savart,
- Note that, like the Coulomb’s law, this is also an inverse square law as
is the distance from the current element to the position where the field is to be calculated. The constant μ0 which appears here is known as the permeability of free space, which has a value
- We will now do some algebraic manipulation of this equation.
- Writing
and summing over the current distribution, the field at the position
given by
- We use the relation
and absorb the minus sign by interchanging the order of the cross product, - In arriving at the last step, we have used the fact that the gradient being with respect to r it has no effect on
and we have used the identity that for a scalar field f and a vector field
- Since the curl operator
does not depend on the integration variable, we can take it outside the integral sign and write,
- As divergence of a curl is zero, we have,
- This is the magnetostatic Gauss’s law. Comparing with the corresponding electrostatic formula
we see that this equation implies non-existence of magnetic monopoles.
- We are aware that a vector field is uniquely given by specifying its divergence and curl. We will now try to find the curl of the magnetic field.
- Using the form of
in eqn. (1) we get on taking curl,
- Use the identity,
- Let us examine each of the terms. The first term can be simplified as follows. We first take the divergence operator inside the integral as the integration is with respect to the primed variable,
where we have written the gradient with respect to the primed variable by incorporating a minus sign because it acts on the difference - Using the identity
- The first term can be converted to a surface integral, using the divergence theorem and the surface can be taken to infinite distances making the integral vanish. The second term also vanishes because of continuity equation. Thus the first tem of eqn. (2) vanishes, leaving us with the second term
- The
operator can be taken inside the integral and as it is derivative with respect to r, it acts only on
- This is known as Ampere’s Law. Thus the magnetic field is specified by
- Note that for the case of electric field, the curl is zero , which is characteristic of a conservative field.
- We will now provide an integral formulation of these two relations.
- Consider a closed volume V defined by a surface S. The normal to the surface is defined in the usual way. We can take the volume integral of the first relation and convert to a surface integral using the divergence theorem.
- This is the integral form of magnetostatic Gauss’s law. Take the second relation. Let S be an arbitrary surface through which the current passes. The surface integral is then given by
- The first relation can be converted to a line integral using the Stoke’s thorem,
- In the following, we illustrate the use of Biot Savart’s law and Ampere’s law.
- Just as direct use of Coulomb’s law for calculation of electric field for a charge distribution was not always easy and we had to restrict our calculation to a few cases where symmetry of the problem allowed us to use Gauss’s law to our advantage, direct use of Biot Savart’s law can be made only in a few cases, though the law is always applicable.
- Ampere’s law provides an attractive alternative for cases where symmetry allows us to express the magnetic field in a form which allows us to use the line integral of the magnetic field in terms of B itself.
Magnetic Field of a Long Straight Wire Carrying Current
- Let us take the wire along the z direction. We will first compute the magnetic field using the integral form of Ampere’s law.
- By symmetry, the field cannot depend on z coordinate and its magnitude can only depend on the distance from the wire.
- Thus, if we take a circle of radius r, the magnetic field strength should be the same everywhere. Further, the direction of the field should be circumferential, i.e. given by the right hand rule.
- If we were to clasp the wire with our right palm, finger pointing in the direction of the current, the direction in which the finger curls is the direction of the magnetic field. (This is dictated by symmetry and we will see more explicitly when we relook at the problem from Biot Savart’s law).
- Taking an Amperian loop in the form of a circle of radius R, the line integral is
- Thus
wherethe unit vector along the azimuthal direction.
- Let us redo the problem using Biot Savart’s law.
- Let us take
along the x-axis which is also the direction of the current. We will calculate the magnetic field at a distance r from the wire along the y-axis.
- Note that this is quite general as from whichever point we want to calculate the magnetic field, we can drop a perpendicular on to the x-axis and call this to be the y axis. Thus the vector
is in the xy plane. We have,
- It is directed along
because the vectors
are in the xy plane. We also have,
which gives - Thus the magnetic field is given by
Field Along the Axis of a Circular Loop
- Let us take the loop in the xy plane. We wish to calculate the field along the z axis. A length element along the circle is given by
and has the position vector
- We take the point P along the z axis so that
With these relations, we have,
- Thus, the magnetic field along the axis is given by
where we have used the magnetic moment vectorgiven by the product of the current with the area of the loop directed along the normal to the loop according to the right hand rule.
- It is observed that at large distances from the loop the magnetic field varies as the inverse cube of distance from the loop,
Solved Examples
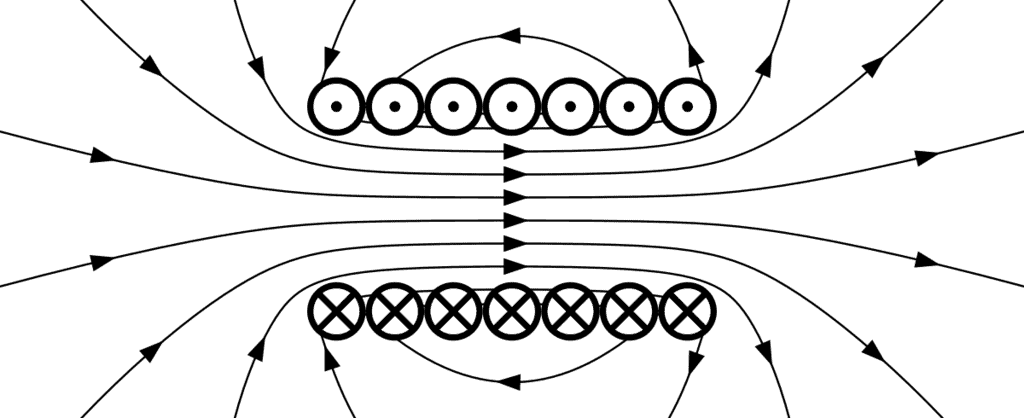
Example.1. Two infinite conducting planes at z=0 and z=d carry currents in opposite directions with surface current density in opposite directions Calculate the magnetic field everywhere in space.
- Let us take the yz plane to be the plane of the paper so that the direction of current flow is perpendicular to this plane. Consider a single conducting plane carrying current in the x direction. Let the plate be in the xy plane. The surface current is shown by a circles with a dot.
- Consider an Amperian loop of length L and width 2z located as shown. The magnetic field direction above the plane is in –y direction while that below is in +y direction. Taking the loop to be anticlockwise, the line integral of magnetic field is
- Thus, above the plane the field is
and below the plane it is
Not that the field strength is independent of the distance from the plane.
- If we have two planes, at z=0 and z=d, the former having a linear current density
the fields would add in the region between the plates and would cancel outside. Between the plates,
and outside both the plates the field is zero.
Example.2. Part of a long current carrying wire is bent in the form of a semicircle of radius R. Calculate the magnetic field at the centre of the semi circle.
- Since the centre is along the line carrying the current,
for the straight line section and the contribution to magnetic field is only due to the semicircular arc.
- The field is into the page at B and is given by Biot Savart’s law to be
Example.3. A long cylindrical wire has a current density flowing in the direction of its length whose density is J = J0r, where r is the distance from the cylinder’s axis. Find the magnetic field both inside and outside the cylinder.
- The total current in the wire can be obtained by integrating the current density over its cross section The current enclosed within a radius r from the axis is
- Using Ampere’s law, the field at a distance is r < R is
- The total current carried by the wire being
the field outside is given by
Example.4. A thin plastic disk of radius R has a uniform charge density σ. The disk is rotating about its axis with an angular speed ω. Find the magnetic field along the axis of the disk at a distance z from the centre.
- The current on the disk can be calculated by assuming the rotating disc to be equivalent to a collection of concentric current loops.
- Consider a ring of radius r and width dr. As the disc rotates, the rotating charge on this annular section behaves like a current loop carrying current
The field at a distance z due to this ring is
- The total field is obtained by integrating this expression from 0 to R,
which can be easily performed by a substitution x = r2 + z2. The result is
Example.5. Two infinite conducting planes at z=0 and z=d carry currents in opposite directions with surface current density in the same directions Calculate the magnetic field everywhere in space.
- The field due to a single plane carrying a linear current density
direction above the plane while below the plane it is in +y direction.
- Since the magnitude of the field is independent of distance, the field cancels between the planes and add up above the planes. For z > d, we have
while for z<0 it is
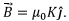
- Its value between the planes is zero.
Example.6. Two infinite conducting sheets lying in x-z and y-z planes intersect at right angles along the z axis. On each plane a surface current Find the magnetic field in each of the four quadrants into which the space is divided by the planes.
- The field due to the current in xz plane is along
the plane (i.e. for y > 0) and along
the plane (i.e. for y < 0)
- Likewise for the y-z plane, the field is along
the plane (i.e. for x > 0) and along
below (x < 0). The magnitude of the field in each case is the same and is
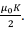
- Thus the field along the first quadrant is
and along the fourth is
One can similarly find the fields in the other two quadrants.
Example.7. Consider the loop formed by two semicircular wires of radii R1 and R2 (>R1) and two short straight sections, as shown. A current I flows through the wire. Find the field at the common centre of the semicircles.
- From example 2 it follows that the contribution to the field due to two straight sections is zero.
- The smaller semicircle section gives a field into the page while the bigger semicircle gives a field out of the page. The net field is (into the page)
Example.8. The current density along a long cylindrical wire of radius a is given by where r is the distance from the axis of the cylinder. Use Ampere’s law to find the magnetic field both inside and outside the cylinder.
- First find the current enclosed within a distance r from the axis,
- Thus the field inside is given by
- Outside the cylinder the total current
|
11 videos|50 docs|56 tests
|
FAQs on Magnetostatics - 1 - Electromagnetic Fields Theory (EMFT) - Electrical Engineering (EE)
| 1. What is magnetostatics? |  |
| 2. What is the difference between current and current density? |  |
| 3. What is Biot-Savart's Law and Ampere's Law? |  |
| 4. How is the magnetic field calculated for a long straight wire carrying current? |  |
| 5. What is the magnetic field along the axis of a circular loop carrying current? |  |