Hydrostatic Thrusts on Submerged Plane Surface - 1 | Fluid Mechanics for Mechanical Engineering PDF Download
Hydrostatic Thrusts on Submerged Plane Surface
Due to the existence of hydrostatic pressure in a fluid mass, a normal force is exerted on any part of a solid surface which is in contact with a fluid. The individual forces distributed over an area give rise to a resultant force.
Plane Surfaces
Consider a plane surface of arbitrary shape wholly submerged in a liquid so that the plane of the surface makes an angle θ with the free surface of the liquid. We will assume the case where the surface shown in the figure below is subjected to hydrostatic pressure on one side and atmospheric pressure on the other side.
Fig 5.1 Hydrostatic Thrust on Submerged Inclined Plane Surface
Let p denotes the gauge pressure on an elemental area dA. The resultant force F on the area A is therefore (5.1)
According to Eq (3.16a) Eq (5.1) reduces to
(5.2)
Where h is the vertical depth of the elemental area dA from the free surface and the distance y is measured from the x-axis, the line of intersection between the extension of the inclined plane and the free surface (Fig. 5.1). The ordinate of the centre of area of the plane surface A is defined as
(5.3)
Hence from Eqs (5.2) and (5.3), we get (5.4)
where hc (yc sin θ) is the vertical depth (from free surface) of centre c of area .
Equation (5.4) implies that the hydrostatic thrust on an inclined plane is equal to the pressure at its centroid times the total area of the surface, i.e., the force that would have been experienced by the surface if placed horizontally at a depth hc from the free surface (Fig. 5.2).
Fig 5.2 Hydrostatic Thrust on Submerged Horizontal Plane Surface
The point of action of the resultant force on the plane surface is called the centre of pressure cp Let xp and yp be the distances of the centre of pressure from the y and x axes respectively. Equating the moment of the resultant force about the x axis to the summation of the moments of the component forces, we have (5.5)
Solving for yp from Eq. (5.5) and replacing F from Eq. (5.2), we can write (5.6)
In the same manner, the x coordinate of the centre of pressure can be obtained by taking moment about the y-axis. Therefore,
From which, (5.7)
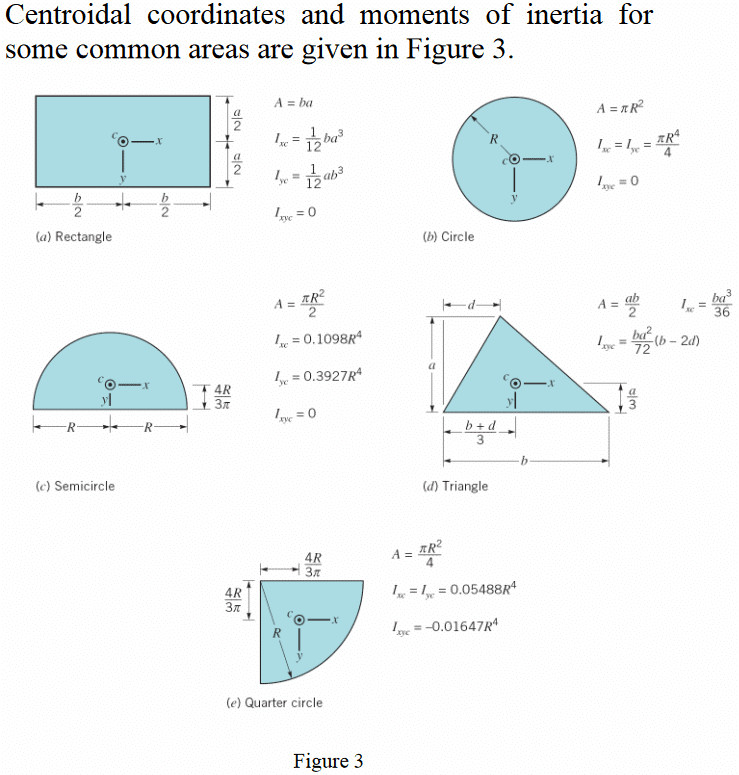
The two double integrals in the numerators of Eqs (5.6) and (5.7) are the moment of inertia about the x-axis Ixxand the product of inertia Ixy about x and y axis of the plane area respectively. By applying the theorem of parallel axis (5.8)
(5.9)
where, I x' x' and I x' y' are the moment of inertia and the product of inertia of the surface about the centroidal axes (x' - y'), xc, and yc are the coordinates of the center c of the area with respect to x-y axes.
With the help of Eqs (5.8), (5.9) and (5.3), Eqs (5.6) and (5.7) can be written as (5.10a)
(5.10b)
The first term on the right hand side of the Eq. (5.10a) is always positive. Hence, the centre of pressure is always at a higher depth from the free surface than that at which the centre of area lies. This is obvious because of the typical variation of hydrostatic pressure with the depth from the free surface. When the plane area is symmetrical about the y' axis, I x' y' = 0, and xp = xc .
Hydrostatic Thrusts on Submerged Curved Surfaces
On a curved surface, the direction of the normal changes from point to point, and hence the pressure forces on individual elemental surfaces differ in their directions. Therefore, a scalar summation of them cannot be made. Instead, the resultant thrusts in certain directions are to be determined and these forces may then be combined vectorially. An arbitrary submerged curved surface is shown in Fig. 5.3. A rectangular Cartesian coordinate system is introduced whose xy plane coincides with the free surface of the liquid and z-axis is directed downward below the x - y plane.
Fig 5.3 Hydrostatic thrust on a Submerged Curved Surface
Consider an elemental area dA at a depth z from the surface of the liquid. The hydrostatic force on the elemental area dA is
d F = p g z dA (5.11)
and the force acts in a direction normal to the area dA. The components of the force dF in x, y and z directions are
Where l, m and n are the direction cosines of the normal to dA. The components of the surface element dA projected on yz, xz and xy planes are, respectively
dAx = ldA (5.13a)
dAy = mdA (5.13b)
dAz = ndA (5.13c)
Substituting Eqs (5.13a-5.13c) into (5.12) we can write
Therefore, the components of the total hydrostatic force along the coordinate axes are
where zc is the z coordinate of the centroid of area Ax and Ay (the projected areas of curved surface on yz and xz plane respectively). If zp and yp are taken to be the coordinates of the point of action of Fx on the projected area Ax on yz plane, , we can write
where Iyy is the moment of inertia of area Ax about y-axis and Iyz is the product of inertia of Ax with respect to axes y and z. In the similar fashion, zp' and x p' the coordinates of the point of action of the force Fy on area Ay, can be written as
where Ixx is the moment of inertia of area Ay about x axis and Ixz is the product of inertia of Ay about the axes x and z.
We can conclude from Eqs (5.15), (5.16) and (5.17) that for a curved surface, the component of hydrostatic force in a horizontal direction is equal to the hydrostatic force on the projected plane surface perpendicular to that direction and acts through the centre of pressure of the projected area. From Eq. (5.15c), the vertical component of the hydrostatic force on the curved surface can be written as (5.18)
where  is the volume of the body of liquid within the region extending vertically above the submerged surface to the free surfgace of the liquid. Therefore, the vertical component of hydrostatic force on a submerged curved surface is equal to the weight of the liquid volume vertically above the solid surface of the liquid and acts through the center of gravity of the liquid in that volume.
is the volume of the body of liquid within the region extending vertically above the submerged surface to the free surfgace of the liquid. Therefore, the vertical component of hydrostatic force on a submerged curved surface is equal to the weight of the liquid volume vertically above the solid surface of the liquid and acts through the center of gravity of the liquid in that volume.
|
56 videos|154 docs|75 tests
|
FAQs on Hydrostatic Thrusts on Submerged Plane Surface - 1 - Fluid Mechanics for Mechanical Engineering
| 1. What is hydrostatic thrust on a submerged plane surface? |  |
| 2. How is hydrostatic thrust calculated on a submerged plane surface? |  |
| 3. What factors affect the hydrostatic thrust on a submerged plane surface? |  |
| 4. How does the shape of the submerged plane surface affect the hydrostatic thrust? |  |
| 5. Can the hydrostatic thrust on a submerged plane surface be negative? |  |

















