Intermittency - 2 | Fluid Mechanics for Mechanical Engineering PDF Download
continued..
Consider another lump of fluid with a negative value of v'. This is arriving at y1 from ( y1 + 1). If this lump retains its original momentum, its mean velocity at the current lamina y1 will be somewhat more than the original mean velocity of y1. This difference is given by
 (33.16)
(33.16)
- The velocity differences caused by the transverse motion can be regarded as the turbulent velocity components at
 .
. - We calculate the time average of the absolute value of this fluctuation as
 (33.17)
(33.17)
- Suppose these two lumps of fluid meet at a layer y1 The lumps will collide with a velocity 2u' and diverge. This proposes the possible existence of transverse velocity component in both directions with respect to the layer at y1. Now, suppose that the two lumps move away in a reverse order from the layer y1 with a velocity 2u'. The empty space will be filled from the surrounding fluid creating transverse velocity components which will again collide at y1. Keeping in mind this argument and the physical explanation accompanying Eqs (33.4), we may state that

along with the condition that the moment at which u' is positive, v' is more likely to be negative and conversely when u' is negative. Possibly, we can write at this stage
 (33.18)
(33.18)
where C1 and C2 are different proportionality constants. However, the constant C2 can now be included in still unknown mixing length and Eg. (33.18) may be rewritten as

- For the expression of turbulent shearing stress τt we may write

- After comparing this expression with the eddy viscosity Eg. (33.14), we may arrive at a more precise definition,
 (33.20a)
(33.20a)
where the apparent viscosity may be expressed as (33.20b)
(33.20b)
and the apparent kinematic viscosity is given by
 (33.20c)
(33.20c)
- The decision of expressing one of the velocity gradients of Eq. (33.19) in terms of its modulus as
 was made in order to assign a sign to τt according to the sign of
was made in order to assign a sign to τt according to the sign of  .
. - Note that the apparent viscosity and consequently,the mixing length are not properties of fluid. They are dependent on turbulent fluctuation.
- But how to determine the value of "l" the mixing length? Several correlations, using experimental results for
 have been proposed to determine l.
have been proposed to determine l.
However, so far the most widely used value of mixing length in the regime of isotropic turbulence is given by
where Y is the distance from the wall and X is known as von Karman constant (≈ 0.4 ).
|
56 videos|104 docs|75 tests
|
FAQs on Intermittency - 2 - Fluid Mechanics for Mechanical Engineering
| 1. What is intermittency in mechanical engineering? |  |
| 2. How does intermittency affect mechanical systems? |  |
| 3. What are the common causes of intermittency in mechanical systems? |  |
| 4. How can intermittency be mitigated in mechanical systems? |  |
| 5. Are there any advancements in technology to address intermittency in mechanical systems? |  |
|
56 videos|104 docs|75 tests
|

|
Explore Courses for Mechanical Engineering exam
|

|
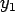 .
. 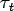 have been proposed to determine l.
have been proposed to determine l. 
















