Introduction to Laminar Boundary Layers - 2 | Fluid Mechanics for Mechanical Engineering PDF Download
Blasius Flow Over A Flat Plate
- The classical problem considered by H. Blasius was
- Two-dimensional, steady, incompressible flow over a flat plate at zero angle of incidence with respect to the uniform stream of velocity U∞.
- The fluid extends to infinity in all directions from the plate.
- Blasius wanted to determine
(a) the velocity field solely within the boundary layer,
(b) the boundary layer thickness(δ),
(c) the shear stress distribution on the plate, and
(d) the drag force on the plate. - The Prandtl boundary layer equations in the case under consideration are

The boundary conditions are

- Note that the substitution of the term
 in the original boundary layer momentum equation in terms of the free stream velocity produces
in the original boundary layer momentum equation in terms of the free stream velocity produces  which is equal to zero.
which is equal to zero. - Hence the governing Eq. (28.15) does not contain any pressure-gradient term.
- However, the characteristic parameters of this problem are U∞, x, v,y that is, u = u U∞, x, v,y
- This relation has five variables U∞, x, v,y .
- It involves two dimensions, length and time.
- Thus it can be reduced to a dimensionless relation in terms of (5-2) =3 quantities ( Buckingham Pi Theorem)
- Thus a similarity variables can be used to find the solution
- Such flow fields are called self-similar flow field .
Law of Similarity for Boundary Layer Flows
- It states that the u component of velocity with two velocity profiles of u(x,y) at different x locations differ only by scale factors in u and y .
- Therefore, the velocity profiles u(x,y) at all values of x can be made congruent if they are plotted in coordinates which have been made dimensionless with reference to the scale factors.
- The local free stream velocity U(x) at section x is an obvious scale factor for u, because the dimensionless u(x) varies between zero and unity with y at all sections.
- The scale factor for y , denoted by g(x) , is proportional to the local boundary layer thickness so that y itself varies between zero and unity.
- Velocity at two arbitrary x locations, namely x1 and x2 should satisfy the equation
 (28.17)
(28.17)
- Now, for Blasius flow, it is possible to identify g(x) with the boundary layers thickness δ we know

Thus in terms of x we get

i.e
 ( 28.18)
( 28.18)
where 
or more precisely,
 (28.19)
(28.19)

The stream function can now be obtained in terms of the velocity components as

 (28.20)
(28.20)
where D is a constant. Also  and the constant of integration is zero if the stream function at the solid surface is set equal to zero.
and the constant of integration is zero if the stream function at the solid surface is set equal to zero.
Now, the velocity components and their derivatives are:
 (28.21a)
(28.21a)

or
 (28.21b)
(28.21b)
 (28.21c)
(28.21c)
 (28.21d)
(28.21d)
 (28.21e)
(28.21e)
Substituting (28.2) into (28.15), we have

or
 (28.22)
(28.22)
where

and 
This is known as Blasius Equation .
Contd. from Previous Slide
The boundary conditions as in Eg. (28.16), in combination with Eg. (28.21a) and (28.21b) become
 (28.23)
(28.23)
Equation (28.22) is a third order nonlinear differential equation .
- Blasius obtained the solution of this equation in the form of series expansion through analytical techniques
- We shall not discuss this technique. However, we shall discuss a numerical technique to solve the aforesaid equation which can be understood rather easily.
- Note that the equation for f does not contain x .
- Boundary conditions at x = 0 and y = ∞ merge into the condition
 . This is the key feature of similarity solution.
. This is the key feature of similarity solution. - We can rewrite Eq. (28.22) as three first order differential equations in the following way
f' = G ( 28.24a)
G = H (28.24b)
 (28.24c)
(28.24c)
- Let us next consider the boundary conditions.
- The condition f (0) = 0 remains valid.
- The condition f' (0) = 0 means that G (0) = 0 .
- The condition f'' (∞) = 1 gives us G (∞) = 1 .
Note that the equations for f and G have initial values. However, the value for H(0) is not known. Hence, we do not have a usual initial-value problem.
Shooting Technique
We handle this problem as an initial-value problem by choosing values of H(0) and solving by numerical methods F (n) , G (n) and H(n) .
In general, the condition G (∞) = 1. will not be satisfied for the function G arising from the numerical solution.
We then choose other initial values of H so that eventually we find an H(0) which results in G (∞) = 1 .
This method is called the shooting technique .
In Eq. (28.24), the primes refer to differentiation wrt. the similarity variable n. The integration steps following Runge-Kutta method are given below.
 (28.25a)
(28.25a)
 (28.25b)
(28.25b)
 (28.25c)
(28.25c)
- One moves from nn +1 =nn . A fourth order accuracy is preserved if h is constant along the integration path, that is, nn +1 - n =h for all values of n . The values of k , l and m are as follows.
- For generality let the system of governing equations be


In a similar way k3 , l3, m3 and k4 , l4, m4 mare calculated following standard formulae for the Runge-Kutta integration. For example, k3 is given by  The functions F1, F2and F3 are G, H , - f/H2 respectively. Then at a distance Δn from the wall, we have
The functions F1, F2and F3 are G, H , - f/H2 respectively. Then at a distance Δn from the wall, we have
 (28.26d)
(28.26d)
- As it has been mentioned earlier F'(0) = H (0) = λ is unknown. It must be determined such that the condition F' (0) = G (∞) = 1 is satisfied.
The condition at infinity is usually approximated at a finite value of n (around n= 10 ). The process of obtaining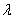 accurately involves iteration and may be calculated using the procedure described below.
accurately involves iteration and may be calculated using the procedure described below.
- For this purpose, consider Fig. 28.2(a) where the solutions of G versus n for two different values of H(0) are plotted.
The values of G(∞) are estimated from the G curves and are plotted in Fig. 28.2(b). - The value of
- H(0) now can be calculated by finding the value
 at which the line 1-2 crosses the line G(∞) = 1 By using similar triangles, it can be said that
at which the line 1-2 crosses the line G(∞) = 1 By using similar triangles, it can be said that  . By solving this, we get
. By solving this, we get  .
. - Next we repeat the same calculation as above by using
 and the better of the two initial values of H(0) . Thus we get another improved value
and the better of the two initial values of H(0) . Thus we get another improved value  . This process may continue, that is, we use
. This process may continue, that is, we use  and
and  as a pair of values to find more improved values for H(0) , and so forth. The better guess for H (0) can also be obtained by using the Newton Raphson Method. It should be always kept in mind that for each value of H(0) , the curve G(n) versus n is to be examined to get the proper value of G(∞) .
as a pair of values to find more improved values for H(0) , and so forth. The better guess for H (0) can also be obtained by using the Newton Raphson Method. It should be always kept in mind that for each value of H(0) , the curve G(n) versus n is to be examined to get the proper value of G(∞) . - The functions f(n), f' (n) = G and f" (n) =H are plotted in Fig. 28.3.The velocity components, u and v inside the boundary layer can be computed from Eqs (28.21a) and (28.21b) respectively.
- A sample computer program in FORTRAN follows in order to explain the solution procedure in greater detail. The program uses Runge Kutta integration together with the Newton Raphson method



- Measurements to test the accuracy of theoretical results were carried out by many scientists. In his experiments, J. Nikuradse, found excellent agreement with the theoretical results with respect to velocity distribution (u/ U∞) within the boundary layer of a stream of air on a flat plate.
- In the next slide we'll see some values of the velocity profile shape f' (n) = (u/ U∞) = G and f" (n) = H in tabular format.
Values of the velocity profile shape f' (n) = (u/ U∞) = G and f" (n) = H


|
56 videos|104 docs|75 tests
|
FAQs on Introduction to Laminar Boundary Layers - 2 - Fluid Mechanics for Mechanical Engineering
| 1. What is a laminar boundary layer? |  |
| 2. How does a laminar boundary layer differ from a turbulent boundary layer? |  |
| 3. What factors influence the development of a laminar boundary layer? |  |
| 4. What are the advantages of a laminar boundary layer in engineering applications? |  |
| 5. Can a laminar boundary layer transition to a turbulent boundary layer? |  |
|
56 videos|104 docs|75 tests
|

|
Explore Courses for Mechanical Engineering exam
|

|

















