General Viscosity Law - 1 | Fluid Mechanics for Mechanical Engineering PDF Download
General Viscosity Law
Newton's viscosity law is

where,
τ = Shear Stress,
n is the coordinate direction normal to the solid-fluid interface,
μ is the coefficient of viscosity, and
V is velocity.
The above law is valid for parallel flows.
Considering Stokes' viscosity law: shear stress is proportional to rate of shear strain so that

τ has two subscripts---
first subscript : denotes the direction of the normal to the plane on which the stress acts, while the
second subscript : denotes direction of the force which causes the stress.
The expressions of Stokes' law of viscosity for normal stresses are

where μ' is a proportionality factor and it is related to the second coefficient of viscosity μ1 by the relationship 
We have already seen that the thermodyamic pressure is 
Now if we add the three equations 24.3(a),(b) and (c) , we obtain,

or
 (24.4)
(24.4)
For incompressible fluids, 
o,  is satisfied eventually. This is known as Thermodynamic pressure.
is satisfied eventually. This is known as Thermodynamic pressure.
For compressible fluids, Stokes' hypothesis is 
- Invoking this to Eq. (24.4), will finally result in
 (same as for incompressible fluid).
(same as for incompressible fluid). - Interesting historical aspects of the Stoke's assumption
 can be found in Truesdell (1952) Truesdell , C.A. "Stoke's Principle of Viscosity", Journal of Rational Mechanics and Analysis, Vol.1, pp.228-231,1952.
can be found in Truesdell (1952) Truesdell , C.A. "Stoke's Principle of Viscosity", Journal of Rational Mechanics and Analysis, Vol.1, pp.228-231,1952. - Generally, fluids obeying the ideal gas equation follow this hypothesis and they are called Stokesian fluids .
- The second coefficient of viscosity, μ1 has been verified to be negligibly small.
Substituting μ for μ' in 24.3a, 24.3b, 24.3c we obtain

In deriving the above stress-strain rate relationship, it was assumed that a fluid has the following properties
- Fluid is homogeneous and isotropic, i.e. the relation between components of stress and those of rate of strain is the same in all directions.
- Stress is a linear function of strain rate.
- The stress-strain relationship will hold good irrespective of the orientation of the reference coordinate system.
The stress components must reduce to the hydrostatic pressure "p" (typically thermodynamic pressure = hydrostatic pressure ) when all the gradients of velocities are zero.
Navier-Strokes Equation
- Generalized equations of motion of a real flow named after the inventors CLMH Navier and GG Stokes are derived from the Newton's second law
- Newton's second law states that the product of mass and acceleration is equal to sum of the external forces acting on a body.
- External forces are of two kinds-
- one acts throughout the mass of the body ----- body force ( gravitational force, electromagnetic force)
- another acts on the boundary---------------------- surface force (pressure and frictional force).
Objective - We shall consider a differential fluid element in the flow field (Fig. 24.1). Evaluate the surface forces acting on the boundary of the rectangular parallelepiped shown below.

Fig. 24.1 Definition of the components of stress and their locations in a differential fluid element
- Let the body force per unit mass be

and surface force per unit volume be
 (24.7)
(24.7)
- Consider surface force on the surface AEHD, per unit area,

[Here second subscript x denotes that the surface force is evaluated for the surface whose outward normal is the x axis]
- Surface force on the surface BFGC per unit area is
- Net force on the body due to imbalance of surface forces on the above two surfaces is
 (since area of faces AEHD and BFGC is dydz)
(since area of faces AEHD and BFGC is dydz)
(24.8)
- Total force on the body due to net surface forces on all six surfaces is
 (24.9)
(24.9)
- And hence, the resultant surface force dF, per unit volume, is
 (since Volume= dx dy dz) (24.10)
(since Volume= dx dy dz) (24.10)
The quantities 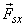 ,
,  and
and 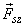 are vectors which can be resolved into normal stresses denoted by
are vectors which can be resolved into normal stresses denoted by  and shearing stresses denoted by
and shearing stresses denoted by  as
as

The stress system has nine scalar quantities. These nine quantities form a stress tensor.
|
56 videos|104 docs|75 tests
|
FAQs on General Viscosity Law - 1 - Fluid Mechanics for Mechanical Engineering
| 1. What is the General Viscosity Law? |  |
| 2. How is viscosity defined in mechanical engineering? |  |
| 3. Why is viscosity important in mechanical engineering? |  |
| 4. How is viscosity measured in mechanical engineering? |  |
| 5. How does temperature affect viscosity? |  |
|
56 videos|104 docs|75 tests
|

|
Explore Courses for Mechanical Engineering exam
|

|

















