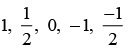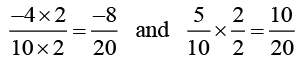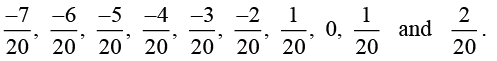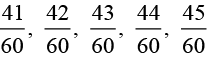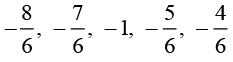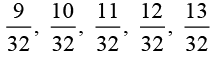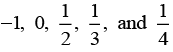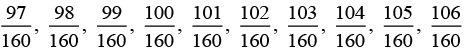NCERT Solutions for Class 8 Maths Chapter 1 - Rational Numbers- 2
In Mathematics, a rational number can be described as a number that can be expressed as a fraction of two integers, where the denominator is not equal to zero. Put differently, any fraction where the numerator and denominator are integers falls under the category of rational numbers. To delve further, let's explore the NCERT Solutions of the chapter.
Let's have a look at NCERT Solutions of Rational Numbers!
Try These
Q1. Write the rational number for each point labelled with a letter.
Ans:
(i) Here, the rational number for the point A is 1/5
The rational number for the point B is 4/5
The rational number for the point C is 5/5 or 1
The rational number for the point D is 8/5
The rational number for the point E is 9/5
(ii) The rational number for:
The point is F -2/6 or 1/3
The point G is -5/6
The point H is -7/6
The point I is -8/6 or -43
The point J is -11/6
Exercise 1.2
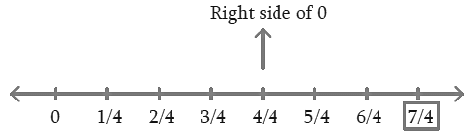
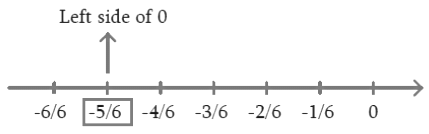
Q.1. Represent these numbers on the number line.
(i) 7/4
(ii) - 5/6
Difficulty level: Medium
Reasoning: The positive numbers are on the right of 0 and negative numbers are represented on the left of 0 in the number line. The denominator of the rational number indicates the number of equal parts into which the first unit has to be divided whereas the numerator indicates as to how many of these parts are to be taken into consideration.
Solution:
7/4 The first unit has to be divided by 4 parts. We make 7 markings of distance
1/4 Each on the right of 0 and starting from 0. The seventh marking represents 7/4Diagram
-5/6 The first unit has to be divided into 6 parts. We make 5 markings of distance 1/6 each on the left of 0 and starting from 0.
The fifth marking represents 5/6 left side of 0.Diagram
Q2. Represent 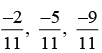 on the number line.
on the number line.
Difficulty level: Medium
Reasoning: The negative numbers are represented on the left of 0 in the number line. The denominator of the rational number indicates the number of equal parts into which the first unit has to be divided whereas the numerator indicates as to how many of these parts are to be taken into consideration.
Solution:
We make 9 marking of distance 1/11 each on the left of 0 and starting from 0.
The second marking represent - 2/11 which is represented as A in the line.
The fifth marking represent -5/11 representations B in the line.
The ninth marking represent -9/11 represented as C in the number line.
Diagram
Q.3. Write five rational numbers which are smaller than 2.
Difficulty level: Easy
What is the known/given?
Rational numbers.
What is the unknown?
The rational numbers between given rational numbers.
Reasoning: We can write infinitely many rational numbers lesser than number 2.
Solution:
Five rational numbers which are smaller than 2 are
Q.4. Find ten rational numbers between -2/5 and 1/2
Difficulty level: Medium
What is the known/given?
Rational numbers.
What is the unknown?
The rational numbers between given rational numbers.
Reasoning:
We can find infinitely many rational numbers between any two given rational numbers by taking the mean of the two rational numbers. Another method: We can make the denominator same for the two given rational numbers.
Solution:
[multiplying both numerator and denominator by 2]
[multiplying both numerator and denominator by 5]
[Multiplying both numerators and denominators by the same number]
Now, there are 9 rational numbers between -4/10 and 5/10, but we need 10 numbers. So, we should again multiply both numerator and denominator by 2 in the two rational numbers -4/10 and 5/10The ten rational numbers between -2/5 and 1/2 which can be taken as.
[There are many more such rational numbers.]
Q.5. Find five rational numbers between,
(i) 2/3 and 4/5
(ii) -3/2 and 5/3
(iii) 1/4 and 1/2
Difficulty level: Medium
What is the known/given?
Rational numbers.
What is the unknown?
The rational numbers between given rational numbers.
Reasoning: We can find infinitely many rational numbers between any two given rational numbers by taking the mean of the two rational numbers.
Another method: We can make the denominator same for the two given rational numbers.
Solution:
(i) 2/3 and 4/5
[multiplying both numerator and denominator by 20]
[multiplying both numerator and denominator by 12]
Answer: The five rational numbers between 2/3 and 4/5 that can be taken are:
Solution:
(ii) 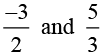
[multiplying both numerator and denominator by 3]
[multiplying both numerator denominator by 2]
Answer:
∴ The five rational numbers between -3/2 and 5/3 that can be taken are:
[There can be more such rational numbers]
(iii) Solution:
1/4 and 1/2
[multiplying both numerator and denominator by 8]
[multiplying both numerator and denominator by 16]
Answer:
Thus, five rational numbers between 1/2 and 1/4 that can be taken are:
Q.6. Write five rational numbers greater than –2.
Difficulty level: Medium
What is the known/given?
Rational numbers.
What is the unknown?
The rational numbers between given rational numbers.
Reasoning: We can find infinitely many rational numbers between any two given rational numbers by taking the mean of the two rational numbers. Another method: We can make the denominator same for the two given rational numbers.
Solution:
Some of the five rational numbers greater than – 2 are
[There can be more such rational numbers]
Q.7. Find the rational numbers between 3/5 and 3/4
Difficulty level: Medium
What is the known/given?
Rational numbers.
What is the unknown?
The rational numbers between given rational numbers.
Reasoning: We can find infinitely many rational numbers between any two given rational numbers by taking the mean of the two rational numbers. Another method: We can make the denominator same for the two given rational numbers.
Solution:
[multiplying both numerator and denominator by 32]
[multiplying both numerator and denominator by 40]
Answer:
Thus, ten rational numbers between 3/5 and 3/4 that can be written are:
[There can be many more such rational numbers]
|
41 videos|48 docs|9 tests
|
FAQs on NCERT Solutions for Class 8 Maths Chapter 1 - Rational Numbers- 2
| 1. What are rational numbers? |  |
| 2. What is the difference between a rational and an irrational number? |  |
| 3. How can we add and subtract rational numbers? |  |
| 4. How can we multiply and divide rational numbers? |  |
| 5. How can we represent rational numbers on a number line? |  |