NCERT Solutions for Class 8 Maths - Practical Geometry - 2
Question 1. Can you construct the following quadrilateral MIST if we have 100° at M instead of 75°?
Solution: Yes, the quadrilateral MIST can be constructed with ∠M = 100° instead of ∠75°.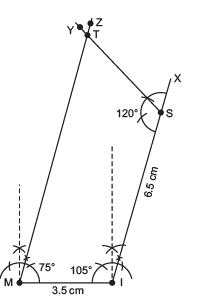
Question 2. Can you construct the quadrilateral PLAN if PL = 6 cm, LA = 9.5 cm, ∠P = 75°, ∠L = 150° and ∠A = 140°?
(Hint: Recall angle-sum property)
Solution: Here, ∠P + ∠L + ∠A + ∠N = 75° + 150° + 140° + ∠N
= 365° + ∠N
But the sum of all the angles of a quadrilateral is 360°.
∴ Construction of quadrilateral PLAN is not possible.
Question 3. In a parallelogram, the lengths of adjacent sides are known. Do we still need measures of the angles to construct as in the Q-1 above?
Solution: No, the measures of three angles are not necessary in case of a parallelogram as its opposite sides are parallel.
EXERCISE 4.1
(Question 1. Construct the following quadrilaterals:
(i) Quadrilateral MORE
MO = 6 cm
OR = 4.5 cm
∠M = 60°
∠O = 105°
∠R = 105°
(ii) Quadrilateral PLAN
PL = 4 cm
LA = 6.5 cm
∠P = 90°
∠A = 110°
∠N = 85°
(iii) Parallelogram HEAR
HE = 5 cm
EA = 6 cm
∠R = 85°
(iv) Rectangle OKAY
OK = 7 cm
KA = 5 cm
Solution: (i) Steps of construction:
I . Draw a line segment MO = 6 cm.
II. At M, draw , such that ∠OMX = 60°.
III. At O, draw , such that ∠MOY = 105°.
IV. From , cut off OR = 4.5 cm.
V. At R, draw , such that ∠ORZ = 105°.
Let intersects
at E.
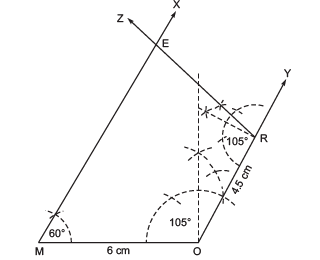
Thus, MORE is the required quadrilateral.
(ii) Steps of construction:
I. Draw a line segment AL = 6.5 cm.
II. At A, draw such that ∠LAX = 110°.
III. At L, draw such that ∠ALY = 75°.
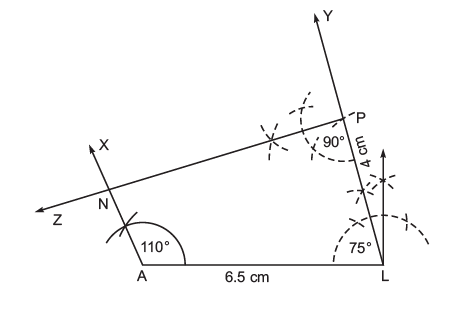
Note: ∠L = 75° is not given, but we can determine it using angle sum property
∵ Sum of the three given angles = 110° + 90° + 85° = 285°
∴ The fourth angle ∠L = 360° – 285° = 75°.
IV. From, cut-off LP = 4 cm.
V. At P, draw such that ∠LPZ = 90°
Let PZ and intersect at N.
Thus, PLAN is the required quadrilateral.
(iii) Steps of construction:
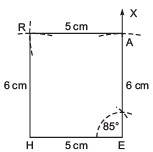
I. Draw a line segment = 5 cm.
II. At E, draw such that ∠HEA = 85°.
III. From , cut-off EA = 6 cm.
IV. With centre at A and radius = 5 cm, draw an arc towards H.
V. With centre at H and radius = 6 cm, draw an arc such that it intersects the previous arc at R.
VI. Join RA and RH.
Thus, HEAR is the required quadrilateral.
(iv) Steps of constructions:
I. Draw a line segment OK = 7 cm.
II. At O, draw such that ∠KOP = 90°.
III. From , cut-off
= 5 cm.
IV. At K, draw such that ∠OKQ = 90°.
V. From cut-off
= 5 cm.
VI. Join A and Y.
Thus, OKAY is the required quadrilateral.
CONSTRUCTION OF A QUADRILATERAL WHEN THREE SIDES AND TWO INCLUDED ANGLES ARE GIVEN
Question. We used some five measurements to draw quadrilateral so far. Can there be different sets of five measurements (other than seen so far) to draw a quadrilateral? The following problems may help you in answering the question.
(i) Quadrilateral ABCD with AB = 5 cm, BC = 5.5 cm, CD = 4 cm, AD = 6 cm and ∠B = 80°.
(ii) Quadrilateral PQRS with PQ = 4.5 cm, ∠P = 70°,∠Q = 100°, ∠ R = 80° and ∠S = 110°.
Construct a few more examples of your own to find sufficiency/insufficiency of the data for construction of a quadrilateral
Solution: (i) It is possible to construct a quadrilateral ABCD with the given measurements.
(ii) Not possible, because we cannot locate the points R and S with the help of given measurements.
EXERCISE 4.4
Question 1 Construct the following quadrilaterals.
(i) Quadrilateral DEAR
DE = 4 cm
EA = 5 cm
AR = 4.5 cm
∠E = 60°
∠A = 90°
(ii) Quadrilateral TRUE
TR = 3.5 cm
RU = 3 cm
UE = 4 cm
∠R = 75°
∠U = 120°
Solution: (i) Steps of construction:
I. Draw a line segment DE = 4 cm.
II. At E, draw such that ∠DEX = 60°.
III. From , cut-off EA = 5 cm.
IV. At A, draw ray such that ∠EAY = 90°.
V. From , cut-off AR = 4.5 cm.
VI. Join R and D.
Thus, DEAR is the required quadrilateral.
(ii) Steps of construction:
I. Draw a line segment = 3.5 cm.
II. At R, draw a ray such that ∠TRX = 75°.
III. From , cut-off RU = 3 cm.
IV. At U, draw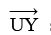 such that ∠RUY = 120°.
such that ∠RUY = 120°.
V. From UY, cut-off= 4 cm.
VI. Join E and T.
Thus, TRUE is the required quadrilateral.
SOME SPECIAL CASES
Using the properties of a square, rectangle, kite and rhombus, etc., we can construct some special quadrilaterals even with less than 5 measurements.
|
276 docs|155 tests
|
FAQs on NCERT Solutions for Class 8 Maths - Practical Geometry - 2
| 1. What is practical geometry? |  |
| 2. How do we construct a perpendicular bisector of a line segment? |  |
| 3. How do we construct an angle bisector? |  |
| 4. Can we construct a triangle if we know the lengths of its three sides? |  |
| 5. How do we construct a parallelogram if we know the lengths of its adjacent sides? |  |






















