Class 8 Exam > Class 8 Notes > Mathematics (Maths) Class 8 > Points to Remember: Squares & Square Roots
Points to Remember: Squares & Square Roots | Mathematics (Maths) Class 8 PDF Download
| Table of contents |
|
| Facts that Matter |
|
| We know that |
|
| Remember |
|
| Properties of Square Number |
|
| Some Interesting Patterns |
|
| Solved Examples |
|
Facts that Matter
- A natural number ‘n’ is a perfect square, if m2 = n for a natural number m.
- A number ending in 2, 3, 7, or 8 is never a perfect square.
- The squares of even numbers are even.
- The squares of odd numbers are odd.
- A number ending in an odd number of zeros is never a perfect square.
- There are 2n non-perfect square numbers between the squares of the numbers n and n + 1.
- For any natural number ‘n’ greater than 1, 2n, (n2 – 1), and (n2 + 1) form a Pythagorean triplet.
- Finding a square root is the inverse operation of squaring a number.
- If ‘n’ be the number of digits of a square number then the number of digits in its square root is given by n/2 (for ‘n’ is even) and (n+1) /2 (for ‘n’ is odd).
Question for Points to Remember: Squares & Square RootsTry yourself:Which of the following is a perfect square?
View Solution
We know that
- If a whole number is multiplied by itself, the product is called the square of that number.
Example: 3 * 3 = 9 = 32
i.e. the square of 3 is 9.
Example: 5 * 5 = 25 = 52
i.e. the square of 5 is 25.
- A natural number is called a perfect square or a square number if it is the square of some natural number.
Example: 16 is the square of 4, therefore, 16 is a perfect square.
Remember
- All-natural numbers are not perfect squares or square numbers, 32 is not a square number. In general, if a natural number ‘m’ can be expressed as n2, where n is also a natural number, then ‘m’ is the perfect square. The numbers like 1, 4, 9, 16, 25, and 36 are called square numbers.
Table: Square of numbers from 1 and 10.
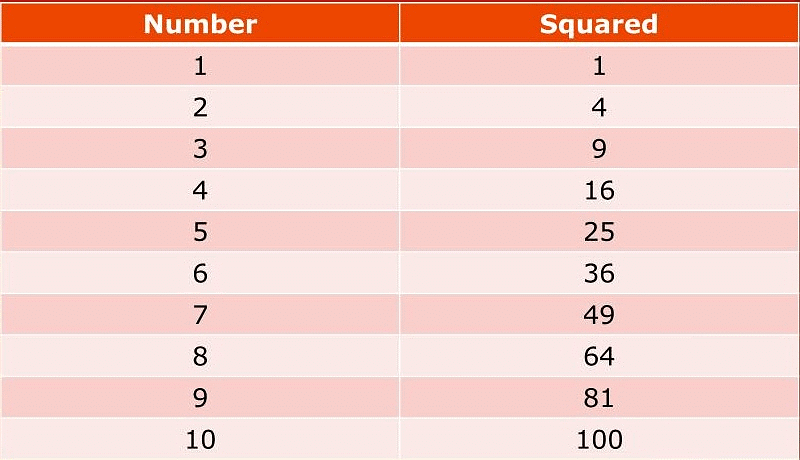
Properties of Square Number
Table: Let us consider the square of all natural numbers from 1 to 20.
From the table, we conclude that:
Property 1: “The ending digits (the digits in the one’s place) of a square number is 0, 1, 4, 5, 6 or 9 only.”
Question for Points to Remember: Squares & Square RootsTry yourself: A perfect square that lies between 40 and 50 is:
View Solution
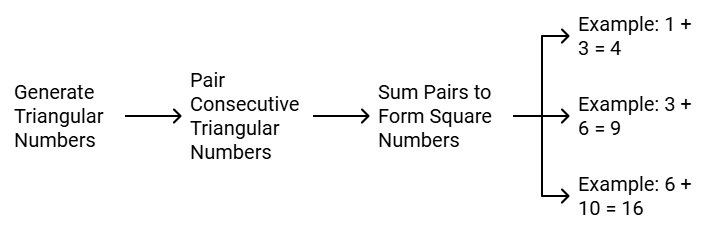
Some Interesting Patterns
- Triangular numbers are: 1, 3, 6, 10, 15, 21, etc. If we combine two consecutive triangular numbers, we get a square number.
1 + 3 = 4, ‘4’ is a square number
3 + 6 = 9, ‘9’ is a square number
6 + 10 = 16, ‘16’ is a square number
and so on.
- 12 =1
112 = 121
1112 = 12321
11112 = 1234321 - 72 = 49
672 = 4489
6672 = 444889
66672 = 44448889 and so on.
Solved Examples
Problem: What will be the unit’s digit in the square of the following numbers?1. 12487
2. 1324
3. 91478
4. 1251
Solution: The unit’s digit in the square of the following is:
1. 12487 is 9 (as 72 = 49, 9 in the unit’s place).
2. 1324 is 6 (as 42 = 16, 6 in the unit’s place).
3. 91478 is 4 (as 82 = 64, 4 in the unit’s place).
4. 1251 is 1 (as 12 = 1, 1 in the unit’s place).
Question for Points to Remember: Squares & Square RootsTry yourself:If 5278 is squared, then what will be at the unit place?
View Solution
Problem: Comment on the square of an even number and of an odd number.
Solution: The square of an even number is always an even number and the square of an odd number is always an odd number. The square of an even number will always have 4, 6, or even zeros in its unit’s place. And the square of an odd number will always have 1, 5, or 9 in its unit’s place.
The document Points to Remember: Squares & Square Roots | Mathematics (Maths) Class 8 is a part of the Class 8 Course Mathematics (Maths) Class 8.
All you need of Class 8 at this link: Class 8
|
79 videos|408 docs|31 tests
|
FAQs on Points to Remember: Squares & Square Roots - Mathematics (Maths) Class 8
| 1. What is a square number and how is it defined? |  |
Ans.A square number is a number that can be expressed as the product of an integer multiplied by itself. For example, \(4\) is a square number because it can be written as \(2 \times 2\). The general form for a square number is \(n^2\) where \(n\) is any whole number.
| 2. How can I find the square root of a number? | |
Ans.To find the square root of a number, you need to determine which number multiplied by itself gives you the original number. For instance, the square root of \(25\) is \(5\) because \(5 \times 5 = 25\). You can also use a calculator or look up a square root table for quick reference.
| 3. What are some properties of square numbers? | |
Ans.Square numbers have several interesting properties:
1. The square of any integer is non-negative.
2. The difference between consecutive square numbers is an odd number (e.g., \(1^2 - 0^2 = 1\), \(2^2 - 1^2 = 3\), \(3^2 - 2^2 = 5\)).
3. The square of an even number is even; the square of an odd number is odd.
| 4. Are there any interesting patterns related to square numbers? | |
Ans.Yes, square numbers display various patterns. For example, the sum of the first \(n\) odd numbers is always a perfect square (\(1 + 3 + 5 + ... + (2n-1) = n^2\)). Additionally, if you list square numbers, you'll notice that they are spaced further apart as numbers increase.
| 5. Can you provide an example of solving a problem involving square roots? | |
Ans.Certainly! If you need to find the square root of \(144\), you can determine that \(12 \times 12 = 144\), so the square root of \(144\) is \(12\). Alternatively, you can check values systematically or use a calculator for larger numbers.
Related Exams
About this Document
|
18.2K Views |
|
4.83/5 Rating |
|
Dec 24, 2024 Last updated |
Document Description: Points to Remember: Squares & Square Roots for Class 8 2024 is part of Mathematics (Maths) Class 8 preparation.
The notes and questions for Points to Remember: Squares & Square Roots have been prepared according to the Class 8 exam syllabus. Information about Points to Remember: Squares & Square Roots covers topics
like Facts that Matter, We know that, Remember, Properties of Square Number, Some Interesting Patterns, Solved Examples and Points to Remember: Squares & Square Roots Example, for Class 8 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Points to Remember: Squares & Square Roots.
Introduction of Points to Remember: Squares & Square Roots in English is available as part of our Mathematics (Maths) Class 8
for Class 8 & Points to Remember: Squares & Square Roots in Hindi for Mathematics (Maths) Class 8 course.
Download more important topics related with notes, lectures and mock test series for Class 8
Exam by signing up for free. Class 8: Points to Remember: Squares & Square Roots | Mathematics (Maths) Class 8
Description
Full syllabus notes, lecture & questions for Points to Remember: Squares & Square Roots | Mathematics (Maths) Class 8 - Class 8 | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) Class 8 | Best notes, free PDF download
Information about Points to Remember: Squares & Square Roots
In this doc you can find the meaning of Points to Remember: Squares & Square Roots defined & explained in the simplest way possible. Besides explaining types of
Points to Remember: Squares & Square Roots theory, EduRev gives you an ample number of questions to practice Points to Remember: Squares & Square Roots tests, examples and also practice Class 8
tests
|
Explore Courses for Class 8 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
Summary
,Semester Notes
,video lectures
,Objective type Questions
,Viva Questions
,Free
,study material
,mock tests for examination
,Points to Remember: Squares & Square Roots | Mathematics (Maths) Class 8
,Points to Remember: Squares & Square Roots | Mathematics (Maths) Class 8
,MCQs
,ppt
,Sample Paper
,Important questions
,Extra Questions
,Previous Year Questions with Solutions
,Points to Remember: Squares & Square Roots | Mathematics (Maths) Class 8
,past year papers
,shortcuts and tricks
,practice quizzes
,Exam
;
Additional Information about Points to Remember: Squares & Square Roots for Class 8 Preparation
Points to Remember: Squares & Square Roots Free PDF Download
The Points to Remember: Squares & Square Roots is an invaluable resource that delves deep into the core of the Class 8 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Points to Remember: Squares & Square Roots now and kickstart your journey towards success in the Class 8 exam.
Importance of Points to Remember: Squares & Square Roots
The importance of Points to Remember: Squares & Square Roots cannot be overstated, especially for Class 8 aspirants.
This document holds the key to success in the Class 8 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Points to Remember: Squares & Square Roots Notes
Points to Remember: Squares & Square Roots Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Points to Remember: Squares & Square Roots.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Points to Remember: Squares & Square Roots Notes on EduRev are your ultimate resource for success.
Points to Remember: Squares & Square Roots Class 8 Questions
The "Points to Remember: Squares & Square Roots Class 8 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 8 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Points to Remember: Squares & Square Roots on the App
Students of Class 8 can study Points to Remember: Squares & Square Roots alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Points to Remember: Squares & Square Roots,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Points to Remember: Squares & Square Roots is prepared as per the latest Class 8 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup