Points to Remember- Exponents and Powers | Mathematics (Maths) Class 8 PDF Download
Important Points to Remember
Exponents and powers are basic ideas in Maths. Knowing these ideas well helps students learn more complex subjects in algebra, calculus, and other Maths areas.
1. What are Exponents?
Exponents are a way to represent repeated multiplication of a number by itself. They are used to simplify expressions and make it easier to understand and work with large numbers or repeated multiplication.
If the base is 2 and we multiply it n times, we have the expression 2n
 Base & ExponentExample: If n = 3, then the expression would be 23.
Base & ExponentExample: If n = 3, then the expression would be 23.
23 = 2 × 2 × 2 = 8
Similarly,
64 = 6 × 6 × 6 × 6
107=10 × 10 × 10 × 10 × 10 × 10 × 10
2. General form of Exponents
The general form of exponents is:
an = a × a × a × a × a × a × a……………. n times
Where:
- a is the base
- n is the exponent (the power to which x is raised)
Powers with Negative Exponents
In mathematics, powers with negative exponents represent the reciprocal or inverse of a number raised to a positive exponent. The negative exponent indicates that the base is in the denominator of a fraction.
To understand negative exponents, let's consider an example using a base, "a," raised to the power of "-n": a(-n) = 1 / (an)
Here, "an" represents the base "a" raised to the power of "n." Taking the reciprocal of "an" gives us the value of "a(-n)." In simpler terms, when you have a negative exponent, you can rewrite it as the reciprocal of the positive exponent.
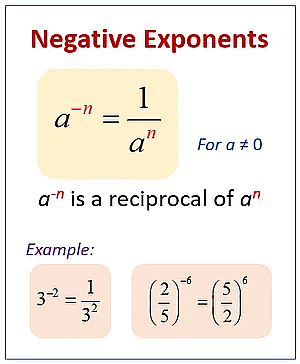 Negative Exponents Let's look at some examples:
Negative Exponents Let's look at some examples:
1. 2(-3) = 1 / (23) = 1 / 8
In this case, 2(-3) is equal to 1/8. The negative exponent turns the base 2 into its reciprocal, which is 1/23 or 1/8.
2. 5(-2) = 1 / (52) = 1 / 25
Here, 5(-2) simplifies to 1/25. The negative exponent converts the base 5 into its reciprocal, resulting in 1/52 or 1/25.
3. (1/3)^(-4) = 3^4 = 81
In this case, (1/3)^(-4) can be rewritten as 3^4, which is equal to 81. The negative exponent removes the reciprocal, and we are left with the base raised to the positive exponent.
Negative exponents often arise in calculations involving fractions or scientific notation. They allow us to express numbers in a more convenient form and simplify calculations.
Remember, negative exponents indicate reciprocals, and positive exponents represent the number raised to the power itself.
3. Laws of Exponents
The laws of exponents, also known as exponent rules or properties, are a set of rules that govern the manipulation and simplification of expressions involving exponents. These laws help us perform operations such as multiplication, division, and raising to powers more efficiently. Here are the main laws of exponents:
Below is table of is the overview of the laws of exponents.
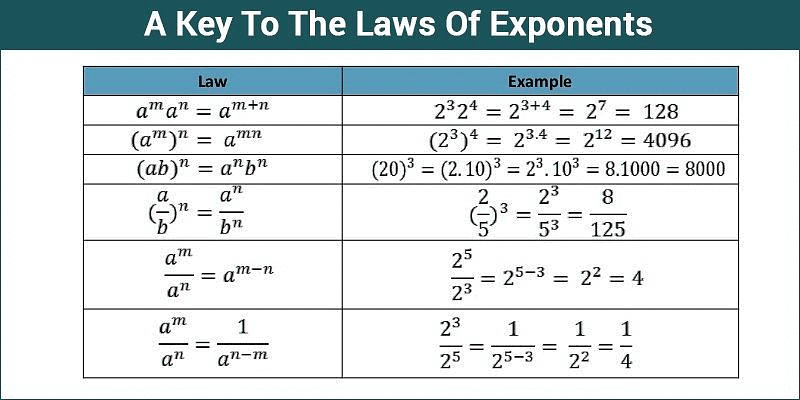
I. Multiplication Law: When multiplying two exponents with the same base and different powers, add the powers and keep the base the same.
am × an = am+n
II. Division Law: When dividing two exponents with the same base and different powers, subtract the denominator's power from the numerator's power and keep the base the same.
am ÷ an = am / an = am-n
III. Power to a Power Law: When raising an exponent to another power, multiply the exponents and keep the base the same.
(am)n = amn
IV. Negative Exponent Law or Multiplicative Inverse: When an exponent has a negative power, take the reciprocal of the base with a positive power.
a-m = 1/am
V. Zero Exponent Law: Any non-zero base raised to the power of zero equals one.
a0 = 1 (where a ≠ 0)
VI. Product to a Power Law: When a product is raised to a power, distribute the power to each factor in the product.
(ab)m = am × bm
VII. Quotient to a Power Law: When a quotient is raised to a power, distribute the power to both the numerator and the denominator.
(a/b)m = am / bm
4. Use of Exponents to Express Small Numbers in Standard Form
Standard Form: A number is said to be in standard form if it is expressed as the product of a number between 1 and 10 (including 1) and a power of 10. It is also known as scientific notation or exponential notation.
Example: 3600000000000 = 36 * 1011 = 3.6 * 1012
So, 3.6 * 1012 is the standard form.
To express a small number in standard form, we need to count the number of decimal places moved and write it as a power of 10.
Example: To express 0.00053 in standard form:
- Move the decimal point 4 places to the right to get 5.3
- Write this as a product of 5.3 and 10 raised to the power of -4 (since we moved the decimal point to the right)
- So, 0.00053 in standard form is 5.3 × 10(-4)
5. Comparing Very Large and Very Small Numbers
One way to compare small and large numbers is to express them in standard form. This makes it easier to compare the numbers based on their exponent values.
Example:
Compare 0.00024 and 0.000042
Convert both numbers to standard form:
- 0.00024 = 2.4 × 10-4
- 0.000042 = 4.2 × 10-5
Now, we can clearly observe that 4.2 × 10-5 is a small number as power of 10 is smaller.
Some Solved Examples
Ques 1: Find the multiplicative inverse of the following.
(i) 2–4
(ii) 10–5
(iii) 7–2
(iv) 5–3
(v) 10–100
Solution:
(i) The multiplicative inverse of 2–4 is 24.
(ii) The multiplicative inverse of 10–5 is 105
(iii) The multiplicative inverse of 7–2 is 72.
(iv) The multiplicative inverse of 5–3 is 53.
(v) The multiplicative inverse of 10–100 is 10100.
Ques 2: Find the value of
Solution: By using rule 2 and 3 –
Ques 3: Solve the following: (-3)2 × (5/3)3
Solution: (-3)2 × (5/3)3
= (-3 × -3) × ( ( 5 × 5 × 5 ) / ( 3 × 3 × 3 ) )
= 9 × (125/27)
= (125/3)
Ques 4: If x11 = y0 and x=2y, then y is equal to
(a) 1/2
(b) 1
(c) -1
(d) -2
Solution: Option A. x11 = y0 => x11 = 1 => x = 1. Given, x = 2y hence, y = x/2 =1/2
overview of the laws of exponents.
|
79 videos|408 docs|31 tests
|
FAQs on Points to Remember- Exponents and Powers - Mathematics (Maths) Class 8
| 1. What are exponents? |  |
| 2. What is the general form of exponents? |  |
| 3. What are the laws of exponents? |  |
| 4. How are exponents used to express small numbers in standard form? |  |
| 5. How can we compare very large and very small numbers using exponents? |  |

|
Explore Courses for Class 8 exam
|

|





















