Algebra of Matrices - Matrices and Determinants, Business Mathematics & Statistics | Business Mathematics and Statistics - B Com PDF Download
Algebra of Matrices
Addition and Subtraction of Matrices
Any two matrices can be added if they are of the same order and the resulting matrix is of the same order. If two matrices A and B are of the same order, they are said to be conformable for addition.
For example:
Note:
-
Only matrices of the same order can be added or subtracted.
-
Addition of matrices is commutative as well as associative.
-
Cancellation laws hold well in case of addition.
-
The equation A + X = 0 has a unique solution in the set of all m × n matrices.
Scalar Multiplication
The matrix obtained by multiplying every element of a matrix A by a scalar λ is called the multiple of A by λ and its denoted by λ A i.e. if A = [aij] then λA = [λaij].
For example:
Note: All the laws of ordinary algebra hold for the addition or subtraction of matrices and their multiplication by scalar.
Multiplication of Matrices
Two matrices can be multiplied only when the number of columns in the first, called the prefactor, is equal to the number of rows in the second, called the postfactor. Such matrices are said to be conformable for multiplication.
where cij = ai1 b1j + ai2 b2j +...+ ain bnj= ∑nk=1 aik bki 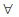 i = 1, 2, 3 ......, m and
i = 1, 2, 3 ......, m and
j = 1, 2, 3 ......, p.
Properties of Multiplication
- Matrix multiplication may or may not be commutative. i.e., AB may or may not be equal to BA
- If AB = BA, then matrices A and B are called Commutative Matrices.
- If AB = BA, then matrices A and B are called Anti-Commutative Matrices.
- Matrix multiplication is Associative
- Matrix multiplication is Distributive over Matrix Addition.
- Cancellation Laws not necessary hold in case of matrix multiplication i.e., if AB = AC => B = C even if A ≠ 0.
- AB = 0 i.e., Null Matrix, does not necessarily imply that either A or B is a null matrix.
Illustration:
show that AB ≠ BA.
Solution:
Here A.B =
and B.A =
Thus A.B ≠ B.A.
Illustration:
Solution:
We have
|
113 videos|175 docs
|
FAQs on Algebra of Matrices - Matrices and Determinants, Business Mathematics & Statistics - Business Mathematics and Statistics - B Com
| 1. What is the purpose of studying matrices and determinants in business mathematics and statistics? |  |
| 2. How are matrices used in business decision-making? |  |
| 3. Can determinants be used to determine if a matrix has an inverse? |  |
| 4. How can matrix operations be applied to statistical analysis in business? |  |
| 5. Are there any limitations or challenges in using matrices and determinants in business mathematics and statistics? |  |
















