Lagrange's Interpolation - Interpolation and Extrapolation, Business Mathematics and Statistics | Business Mathematics and Statistics - B Com PDF Download
Lagrange's Interpolation formula
In this section, we shall obtain an interpolating polynomial when the given data has unequal tabular points. However, before going to that, we see below an important result.
THEOREM 12.3.1 The kth divided difference 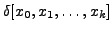 can be written as:
can be written as:
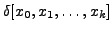 =
= 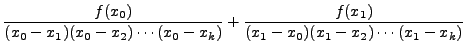
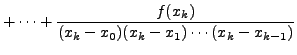
= 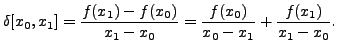
Proof. We will prove the result by induction on k The result is trivially true for k = 0 For k = 1
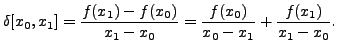
Let us assume that the result is true for k = n i.e.,
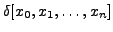 =
= 
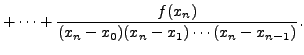
Consider k = n + 1 then the (n + 1)th divided difference is
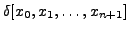 =
= 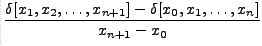
= 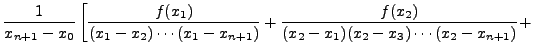
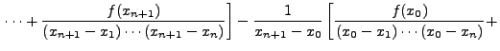
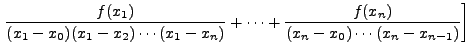
which on rearranging the terms gives the desired result. Therefore, by mathematical induction, the proof of the theorem is complete. height6pt width 6pt depth 0pt
Remark 12.3.2 In view of the theorem 12.3.1 the kth divided difference of a function f(x) remains unchanged regardless of how its arguments are interchanged, i.e., it is independent of the order of its arguments.
Now, if a function is approximated by a polynomial of degree n, then , its (n+1)th divided difference relative to x, xo ,x1,.......,xn will be zero,(Remark 12.2.6) i.e.,
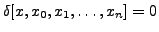
Using this result, Theorem 12.3.1 gives
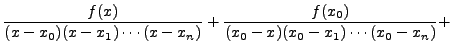
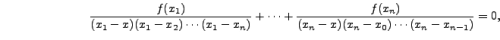
or,
 =
= 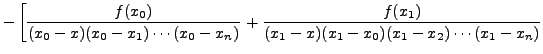
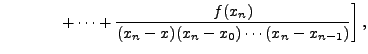
which gives ,
f(x) = 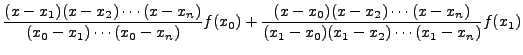
+ 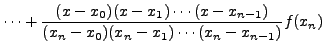
= 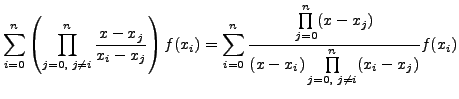
= 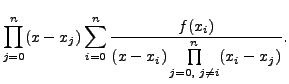
Note that the expression on the right is a polynomial of degree n and takes the value f (xi) at x = xi for i = 0,1,......, (n-1)
This polynomial approximation is called LAGRANGE'S INTERPOLATION FORMULA.
Remark 12.3.3 In view of the Remark (12.2.9), we can observe that Pn (x) is another form of Lagrange's Interpolation polynomial formula as obtained above. Also the remainder term Rn+1 gives an estimate of error between the true value and the interpolated value of the function.
Remark 12.3.4 We have seen earlier that the divided differences are independent of the order of its arguments. As the Lagrange's formula has been derived using the divided differences, it is not necessary here to have the tabular points in the increasing order. Thus one can use Lagrange's formula even when the points x, xo ,x1,.....,xk.......,xn are in any order, which was not possible in the case of Newton's Difference formulae.
Remark 12.3.5 One can also use the Lagrange's Interpolating Formula to compute the value of x for a given value of y = f(x)This is done by interchanging the roles of x and y, i.e. while using the table of values, we take tabular points as yk and nodal points are taken as xk,
EXAMPLE 12.3.6 Using the following data, find by Lagrange's formula, the value of f(x) at x = 10
|
|
0 |
1 |
2 |
3 |
4 |
|
|
9.3 |
9.6 |
10.2 |
10.4 |
10.8 |
|
|
11.40 |
12.80 |
14.70 |
17.00 |
19.80 |
Also find the value of  where f(x) = 16.00
where f(x) = 16.00
Solution: To compute f(10), we first calculate the following products:
 =
= 
= 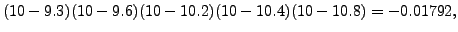
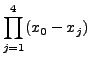 =
= 
 =
= 
Thus,
f(10) ≈ 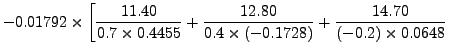
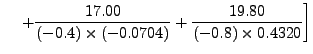
= 13.197845
Now to find the value of  such that f (x) = 16 we interchange the roles of
such that f (x) = 16 we interchange the roles of  and y and calculate the following products:
and y and calculate the following products:
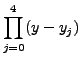 =
= 
= 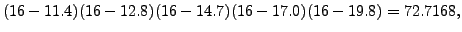
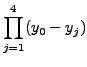 =
= 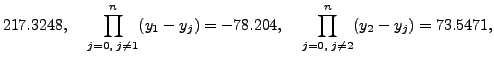
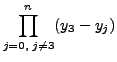 =
= 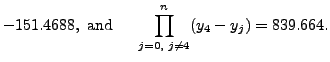
Thus,the required value of  is obtained as:
is obtained as:
x ≈ 

≈ 10.39123
EXERCISE 12.3.7 The following table gives the data for steam pressure  vs temperature
vs temperature  :
:
|
|
360 |
365 |
373 |
383 |
390 |
|
|
154.0 |
165.0 |
190.0 |
210.0 |
240.0 |
Compute the pressure at 
EXERCISE 12.3.8 Compute from following table the value of y for  :
:
|
|
5.60 |
5.90 |
6.50 |
6.90 |
7.20 |
|
|
2.30 |
1.80 |
1.35 |
1.95 |
2.00 |
Also find the value of  where y = 1.00
where y = 1.00
|
115 videos|142 docs
|
FAQs on Lagrange's Interpolation - Interpolation and Extrapolation, Business Mathematics and Statistics - Business Mathematics and Statistics - B Com
| 1. What is Lagrange's interpolation method? |  |
| 2. How does Lagrange's interpolation method work? |  |
| 3. What is the difference between interpolation and extrapolation? |  |
| 4. How can Lagrange's interpolation method be applied in business mathematics? |  |
| 5. What are the limitations of Lagrange's interpolation method? |  |

|
Explore Courses for B Com exam
|

|
























