Questions: Linear Algebra and Matrices - Mathematical Methods of Physics, UGC - NET Physics | Physics for IIT JAM, UGC - NET, CSIR NET PDF Download
Question 1. Let Mn be the vector space of all n × n matrices with real entries under usual matrix addition and scalar multiplication. Find the dimensions of the fol lowing subspaces of Mn:
1. W1 = {A ∈ Mn : A is symmetric}
2. W2 = {A ∈ Mn : A is skew-symmetric}
3. W3 = {A ∈ Mn : A is upper triangular}
4. W4 = {A ∈ Mn : A is tridiagonal}
Sol:
To solve this problem, let's calculate the dimensionof each subspace of Mnn × n matrices with real entries. The dimension of Mnis n2n2entries in a general
1. Subspace (W1 = A ∈ Mn : A is symmetric)
A matrix A = [aij]∈ Mn is symmetric if A = AT , meaning aij = aji for all i, j.
In a symmetric matrix:
- The diagonal entries aii can take any value (n independent entries).
- For i < j, the upper triangular entries aij determine the lower triangular entries aji , leading to
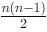 independent entries.
independent entries.
Total number of independent entries: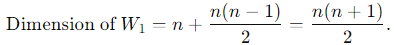
2. Subspace (W2 = A ∈ Mn : A is skew-symmetric)
A matrix A= [aij]∈ Mn is skew-symmetric if AT= −A, meaning aij = −aji for all i, j, and aii = 0 (diagonal entries are zero).
- In a skew-symmetric matrix:
The diagonal entries aii = 0 (n constraints).
For i < j, the upper triangular entries aij determine the lower triangular entries aji = −aij, giving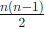 independent entries.
independent entries.
Total number of independent entries: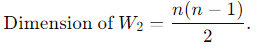
3. Subspace (W3 = A ∈ Mn : A is uper triangular)
A matrix A = [aij] ∈ Mn is upper triangular if aij = 0 for all i > j.
In an upper triangular matrix:
- All entries aij for i ≤ j are independent (1 + 2+ ⋯ + n
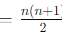 entries).
entries). - The remaining entries (aij for i > j) are zero and do not contribute to the dimension.
Total number of independent entries: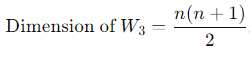
4. Subspace (W4 = A ∈ Mn : A is tridiagonal)
A matrix A = [aij] ∈ Mn is tridiagonal if aij = 0 for all ∣i − j∣ > 1.
In a tridiagonal matrix:
There are n diagonal entries (aii).
- There are n − 1 upper diagonal entries (ai, i + 1).
- There are n − 1 lower diagonal entries (ai + 1,i).
- Total number of independent entries:
Dimension of W4 = n + (n − 1) + (n − 1) = 3n − 2.
Final Dimensions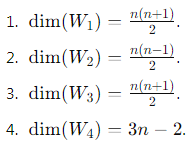
Question 2. Let V be the subspace of M2(R) consisting of matrices such that the entries of the first row add up to zero. Write down a basis for V.
Sol:
Subspace V Definition
Let 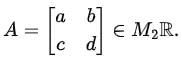
The condition for A ∈ V is:
a + b = 0(the sum of the entries in the first row is zero).
This implies b = −a. Thus, matrices in V can be written as: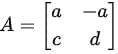 , where
, where 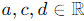 .
.
Dimension of V
The general form of A shows that it depends on three parameters: a, c, and d. Therefore, dim (V) = 3.
Basis for V
To find a basis, we express A as a linear combination of matrices where each parameter (a, c ,d) is varied independently.
Write: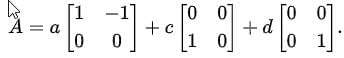
Thus, the following matrices form a basis for V: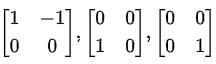 Verification
Verification
- The three matrices are linearly independent because no linear combination of them produces the zero matrix unless all coefficients are zero.
- They span V, as any matrix in V can be written as a linear combination of these matrices.
Question 3. Write down a necessary and sufficient condition, in terms of a, b, c and d (which are assumed to be real numbers), for the matrix not to have a real eigenvalue.
Sol:
To determine a necessary and sufficient condition for the matrix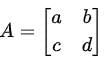
not to have a real eigenvalue, we analyze the eigenvalues of A using the characteristic equation.
1. Eigenvalues of A:
The eigenvalues of A are the roots of its characteristic polynomial, given by:
det(A − λI) = 0,
where I is the identity matrix. Explicitly: 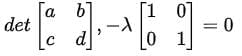
This simplifies to: 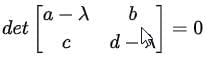
The determinant is:
(a − λ)(d − λ) − bc = 0.
Expanding this, we get the quadratic equation:
λ2 − (a + d)λ + (ad − bc) = 0.
2. Condition for Real Eigenvalues:
The roots of this quadratic equation are real if and only if the discriminant of the quadratic equation is non-negative. The discriminant is:
Δ = (a + d)2 − 4(ad − bc).
Simplifying:
Δ = (a + d)2 − 4ad + 4bc = (a − d)2 + 4bc.
- For the eigenvalues not to be real, the discriminant must be negative:
Δ < 0
3. Necessary and Sufficient Condition:
The necessary and sufficient condition for A not to have real eigenvalues is:
(a − d)2 + 4bc < 0.
4. Interpretation:
(i) (a − d)2 ≥ 0 (since it is a square term).
(ii) For Δ < 0, the term 4bc must be negative and sufficiently large in magnitude to make (a − d)2 + 4bc < 0.
This implies:
- bc < 0 (the product of b and c must be negative).
Thus, the matrix A will not have real eigenvalues if and only if:
bc < 0 and ∣4bc∣ > (a − d)2.
Question 4. Given that the matrixhas 1 as an eigenvalue, compute its trace and its determinant.
Sol:
We are given the matrix: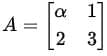
and the information that 1 is an eigenvalue of A. We need to compute the trace and determinant of A.
Step 1: Eigenvalue Condition
The eigenvalues of A satisfy the characteristic equation:
det(A − λI) = 0,
where I is the 2 × 2 identity matrix. For A − λI, we have: 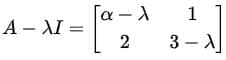
The determinant of A − λI is: 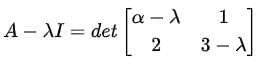
Using the determinant formula, we compute:
det (A − λI) = (α − λ)(3 − λ) − (1)(2).
Simplify:
det (A − λI) = (α − λ)(3 − λ) − 2 = α(3 − λ) − λ(3 − λ) − 2.
Expanding further:
det (A − λI) = 3α − αλ − 3λ + λ2 − 2.
Rearranging:
det(A − λI) = λ2 −(α + 3)λ + (3α − 2).
Since 1 is an eigenvalue, it satisfies the characteristic equation:
12 −(α + 3)(1) + (3α − 2) = 0.
Simplify:
1 − α − 3 + 3α − 2 = 0.
Solve for α:
α = 2.
Step 2: Compute the Trace
The trace of a matrix is the sum of its diagonal elements:
Trace (A) = α + 3.
Substitute α = 2:
Trace (A) = 2 + 3 = 5.
Trace(A) = 2 + 3 = 5.
Step 3: Compute the Determinant
The determinant of A is:
det (A) = α(3) − (1)(2).
Substitute α = 2:
det (A) = 2(3) − 2 = 6 − 2 = 4.
Final Answer:
- Trace: 5
- Determinant: 4
Question 5. Let A be a non diagonal 2 × 2 matrix with complex entries such that A = A−1. Write down its characteristic and minimal polynomials.
Sol:
We are tasked with finding the characteristic and minimal polynomials for a 2 × 2 non-diagonal matrix A with complex entries, satisfying the condition A = A−1.
Step 1: Properties of A = A−1
1. The condition A = A−1 implies:
A2 = I,
where I is the 2 × 2 identity matrix.
2. This means that A is involutory, i.e., squaring the matrix yields the identity matrix.
3. The eigenvalues of A are the roots of its characteristic polynomial. Since A2 = I, any eigenvalue λ of A satisfies: λ2 = 1.
Thus, the eigenvalues are λ = 1 and λ = −1.
Step 2: Characteristic Polynomial
The characteristic polynomial of a 2 × 2 matrix A is defined as:
p(λ) = det(A − λI).
From Step 1, the eigenvalues of A are 1 and −1. Thus, the characteristic polynomial is:
p(λ) = (λ − 1)(λ + 1).
Simplify: p(λ) = λ2 − 1.
Step 3: Minimal Polynomial
The minimal polynomial of A is the monic polynomial of the smallest degree that annihilates A, i.e., m(A) = 0.
From the property A2 = I, it is clear that A satisfies
A2− I = 0.
Thus, the minimal polynomial is: m(λ) = λ2 −1.
Step 4: Non-diagonal Condition
For A to be non-diagonal, it must not commute with all matrices in  . A simple example of such a matrix is:
. A simple example of such a matrix is: 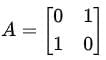
This matrix satisfies A2 = I, is non-diagonal, and has eigenvalues 1and −1.
Final Answer
- Characteristic Polynomial: p(λ) = λ2 −1.
- Minimal Polynomial: m(λ) = λ2 −1.
Question 6. For a fixed positive integer n ≥ 3, let A be the n × n matrix defined by A = I −, where J is the n × n matrix with all entries equal to 1. Which of the fol lowing statements is not true?
1. Ak = A for every positive integer k.
2. Trace(A) = n − 1
3. Rank(A) + Rank(I − A) = n
4. A is invertible.
Sol:
Let us analyze the properties of the given matrix 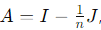 , where J is the n × n matrix with all entries equal to 1.
, where J is the n × n matrix with all entries equal to 1.
Key Properties of J:
1. J is an n × n matrix where all entries are 1.
2. The rank of J is 1, because all rows (or columns) of J are identical.
3. The eigenvalues of J are:
- n, corresponding to the eigenvector [1, 1,…,1] T .
- 0, with multiplicity n − 1, corresponding to eigenvectors orthogonal to [1, 1, …,1]T.
Eigenvalues of A:
1. Since 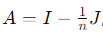 the eigenvalues of A are obtained by shifting the eigenvalues of J:
the eigenvalues of A are obtained by shifting the eigenvalues of J:
- If λ is an eigenvalue of J, then
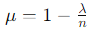 is an eigenvalue of A.
is an eigenvalue of A.
2. The eigenvalues of J are n (once) and 0 (multiplicity n − 1):
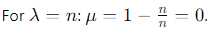
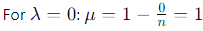 (multiplicity n − 1).
(multiplicity n − 1).
Thus, the eigenvalues of A are 0 (once) and 1 (multiplicity n − 1).
Analyzing the Statements:
1. Ak = A for every positive integer k:
Since A has eigenvalues 0 and 1, raising A to any power k does not change its eigenvalues. Specifically: 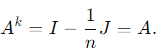
This statement is true.
2. Trace(A) = n − 1:
- The trace of A is the sum of its eigenvalues. From the eigenvalue analysis, A has 0 (once) and 1 (n − 1 times). Thus:
Trace(A) = 0 + (n − 1)(1) = n − 1. - This statement is true.
3. Rank(A) + Rank(I − A) = n:
- The rank of A is equal to the number of nonzero eigenvalues, which is n − 1 (corresponding to eigenvalue 1).
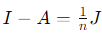 , and its rank is 1 (since J has rank 1).
, and its rank is 1 (since J has rank 1).- Hence: Rank (A) + Rank (I − A) = (n − 1) + 1 = n.
- This statement is true.
4. A is invertible:
A is not invertible because it has 0 0 as an eigenvalue, which makes its determinant 0 0. This statement is false.
Final Answer:
The statement that is not true is:
4. A is invertible.
Question 7. Let A be a 5 × 4 matrix with real entries such that Ax = 0 if and only if x = 0, where x is a 4 × 1 vector. Then find the rank of A.
Sol:
We are given that A is a 5 × 4 matrix with real entries, and the condition Ax = 0 if and only if x = 0, where x is a 4 × 1 vector.
We need to find the rank of A.
Key Observations:
1. Condition Ax = 0 implies x = 0:
This means that the null space (kernel) of A contains only the zero vector.
Thus, the nullity of A is zero.
2. Rank-Nullity Theorem: For any matrix A of size m × n, the rank-nullity theorem states:
Rank(A) + Nullity(A) = n,
where n is the number of columns of A.
Here, n = 4, and since the nullity is zero:
Rank (A) = 4.
3. Rank of A:
- The rank of A is 4, which means A has full column rank (all 4 columns are linearly independent).
- Since A is a 5 × 4 matrix, having rank 4 4 is the maximum possible for the number of columns.
Final Answer:
The rank of A is: 4
Question 8. Consider the following row vectors
a1 = (1, 1, 0, 1, 0, 0), a2 = (1, 1, 0, 0, 1, 0),
a3 = (1, 1, 0, 0, 0, 1) a4 = (1, 0, 1, 1, 0, 0),
a5 = (1, 0, 1, 0, 1, 0), a6 = (1, 0, 1, 0, 0, 1)
What is the dimension of the real vector space spanned by these vectors?
Sol:
To determine the dimension of the real vector space spanned by the given row vectors: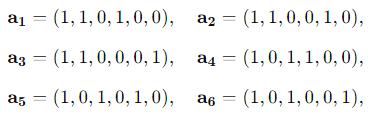
Step 1: Form the Matrix
We arrange the vectors as rows in a matrix A: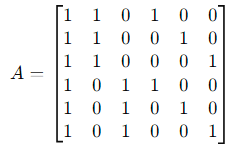
Step 2: Row Reduce the Matrix To find the dimension of the vector space spanned by these vectors, we compute the rank of A by row reducing it to row echelon form.
1. Subtract the first row from rows 2–6: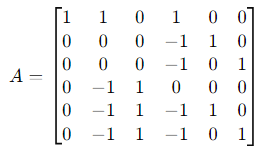
2. Simplify further by eliminating duplicate rows and linear combinations. After row reduction, the matrix reduces to: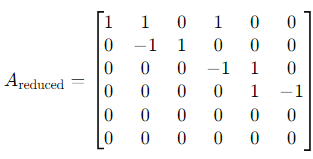
Step 3: Count the Pivot Columns
The row echelon form has 4 non-zero rows, corresponding to 4 pivot columns. This implies that the vectors span a 4-dimensional space. Final Answer:
The dimension of the real vector space spanned by these vectors is: 4
Question 9. Let 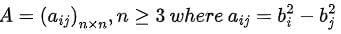 i, j = 1, 2, . . . , n for some distinct real numbers b1 , b2 , . . . , bn . Then find det(A).
i, j = 1, 2, . . . , n for some distinct real numbers b1 , b2 , . . . , bn . Then find det(A).
Solution. Performing the elementary operations, Ri → Ri − R1 for each i = 2, 3, . . . , n we see that det(A) = 0. Note that det(A) may not be zero if n = 2.
Question 10. Number of matrices with real entries, of the formsuch that A2 − A = 0 i
1. only one
2. only two
3. finitely many
4. infinitely many
Solution. Using the equation A2 = A, it can be shown that any matrix A of the form A = where bc = a − a2 , satisfies the given condition. So, there are infinitely many such matrices.
Question 11. Let V be a vector space of dimension n over the field Zp where p is a prime. Then how many elements are there in V ?
Solution. Since dim(V ) = n, so let {e1 , e2 , . . . , en } be a basis of V . Then any element of V is a linear combination of the form αi ei where αi ∈ Zp . So,
the number of elements in V is pn .
Question 12. If T :be a linear transformation defined by T (1, 0, 0) = (1, 0, 1), T (0, 1, 0) = (0, 0, 1) and T (0, 0, 1) = (1, 0, 0). Then find the range space of T , null space of T , rank and nullity of T.
Sol:
To solve this problem, let 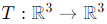 be a linear transformation defined by:
be a linear transformation defined by:
T(1, 0, 0) = (1, 0, 1), T(0, 1, 0) = (0, 0, 1), T(0, 0, 1) = (1, 0, 0).
We need to find:
1. The range space of T,
2. The null space of T,
3. The rank of T,
4. The nullity of T.
Step 1: Representing T as a Matrix
The action of T on the standard basis vectors e1 =(1, 0, 0), e2 = (0, 1, 0), e3 = (0, 0, 1) gives us the columns of the matrix representation of T.
T(e1) = (1, 0, 1), T(e2) = (0, 0, 1), T(e3) = (1, 0, 0).
Thus, the matrix representation of T is: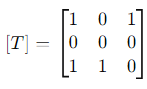
Step 2: Range Space of T
The range space (or column space) of T is spanned by the columns of the matrix: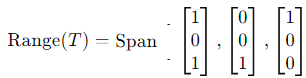
These vectors are linearly dependent, as: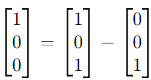
Thus, the range space is spanned by: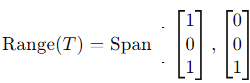
The range space is 2-dimensional.
Step 3: Null Space of T
The null space (or kernel) of T is the set of vectors x ∈ R3 such that T(x) = 0. Solving:
T(x) = [T]⋅x = 0,
where: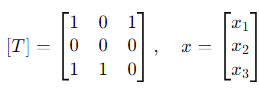
This gives the system of equations:
1. x1 + x3 = 0
2. 0 = 0, (no condition),
3. x1 + x2 = 0.
From these equations: x3 = −x1 , x2 = −x1 .
Let x1 = t. Then:
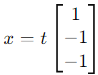
Thus, the null space is: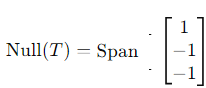
Step 4: Rank and Nullity
From the Rank-Nullity Theorem:
Rank (T) + Nullity (T) = n,
where n = 3.
- The rank is the dimension of the range space: Rank (T) = 2.
- The nullity is the dimension of the null space: Nullity(T) = 1.
Final Answers:
1. Range space of T: 
2. Null space of T: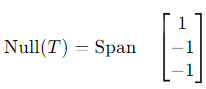
3. Rank of T:
Rank (T) = 2.
4. Nullity of T:
Nullity (T) = 1.
Question 13. Let A ∈ M2(R) such that tr(A) = 2 and det(A) = 3. Write down the characteristic polynomial of A−1 .
Sol:
We are given a matrix 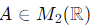 such that:
such that:
tr(A) = 2, det(A) = 3.
We are tasked with finding the characteristic polynomial of A−1.
Step 1: Characteristic Polynomial of A
The characteristic polynomial of A is given by:
pA (λ) = det(A − λI).
For a 2 × 2 matrix A, the characteristic polynomial is:
pA (λ) = λ2 − tr(A)λ + det(A).
Substitute the given values tr (A) = 2 and det (A) = 3:
pA (λ) = λ2 − 2λ + 3.
Step 2: Relationship between A and A−1
If λ is an eigenvalue of A, then 1/λ is an eigenvalue of A−1. The characteristic polynomial of A−1 can be derived from that of A.
Let the eigenvalues of A be λ1 and λ2. Then:
The trace of A satisfies: λ1 + λ2 = tr(A) = 2,
The determinant of A satisfies: λ1 λ2 = det(A) = 3.
The characteristic polynomial of A−1 has eigenvalues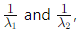 so:
so: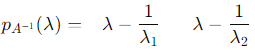
Step 3: Expressing pA−1 (λ)
1. The trace of A −1 is the sum of its eigenvalues: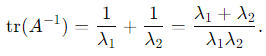
Substitute λ1 + λ2 = 2 and λ1 λ2 = 3: 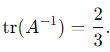 2. The determinant of A−1 is the product of its eigenvalues:
2. The determinant of A−1 is the product of its eigenvalues: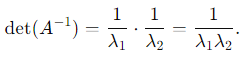
Substitute λ1λ2 = 3: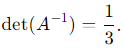
Thus, the characteristic polynomial of A−1 is: 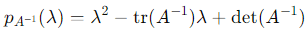
Substitute tr (A−1) = 2/3 and det (A−1) = 1/3:
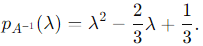
Final Answer:
The characteristic polynomial of A−1 is:
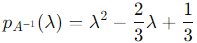
Question 14. Let a 3 × 3 matrix A have eigenvalues 1, 2, −1, then find the trace of the matrix B = A − A−1 + A2 .
Sol:
We are tasked with finding the trace of the matrix B = A − A−1 + A2, where the 3 × 3 matrix A has eigenvalues 1, 2, −1.
Step 1: Properties of Trace and Eigenvalues
1. Trace of A: The trace of a matrix is the sum of its eigenvalues. Since the eigenvalues of A are 1, 2, −1:
tr(A) = 1 + 2 − 1 = 2.
2. Eigenvalues of A−1: If λ is an eigenvalue of A, then 1/λ is an eigenvalue of A−1. Thus, the eigenvalues of A−1 are: 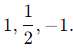
3. Eigenvalues of A2 : If λ is an eigenvalue of A, then λ2 is an eigenvalue of A2.
Thus, the eigenvalues of A2 are:
12 = 1, 22 = 4, (−1)2 = 1.
Step 2: Trace of B
The trace of B is the sum of the traces of A, A−1 , and A2 :
tr(B) = tr(A) − tr(A−1) + tr(A2).
1. Trace of A: tr(A)=2.
2. Trace of A−1: The trace of A−1 is the sum of its eigenvalues: 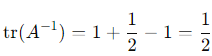
3. Trace of A2: The trace of A2 is the sum of its eigenvalues:
tr(A2) = 1 + 4 + 1 = 6.
Thus:
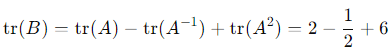
Step 3: Simplify the Result 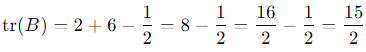
Final Answer:
tr (B) = 15/2
Question 15. The eigenvectors of a 3 × 3 matrix A corresponding to the eigenvalues 1, 1, 2 are (1, 0, −1)T , (0, 1, −1)T and (1, 1, 0)T . Find the matrix A.
Sol:
We are tasked with finding the 3 × 3 matrix A, given its eigenvalues and corresponding eigenvectors.
The eigenvalues are 1, 1 ,2, and the corresponding eigenvectors are:
1. For eigenvalue 1: 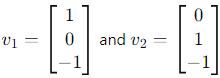 ,
,
2. For eigenvalue 2: 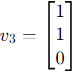
Step 1: Diagonalization
The matrix A can be diagonalized as: A = PDP −1,
where:
- P is the matrix whose columns are the eigenvectors of A,
- D is the diagonal matrix with eigenvalues on its diagonal.
Step 2: Construct P and D
1. Construct the matrix P using the eigenvectors as columns:
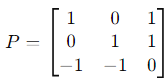
2. Construct the diagonal matrix D using the eigenvalues: 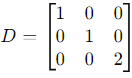
Step 3: Compute P −1
To compute P −1 , use the formula for the inverse of a 3×3 matrix: 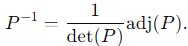
Compute det (P): 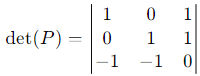
Expanding along the first row: 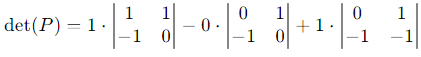
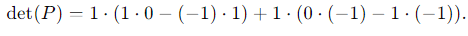
det(P) = 1⋅1 + 1⋅1 = 2.
Compute P−1:
The adjugate of P, adj (P), is computed by finding the cofactors of P. For brevity:
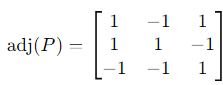
Thus: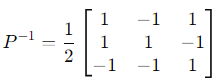
Step 4: Compute A = PDP −1
Substitute P, D, and P−1 into A = PDP−1: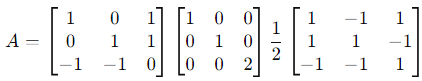
After performing the matrix multiplication: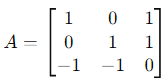
Final Answer:
The matrix A is:
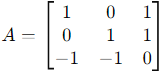
Question 16. What is the null space of the matrix A =
Sol:
We are tasked with finding the null space of the matrix:
A = [ 1 0 2 5 1 4 ].
Step 1: Definition of Null Space
The null space of a matrix A consists of all column vectors x such that:
Ax = 0.
Here, x is a vector in 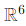 (since A has 6 columns), so
(since A has 6 columns), so 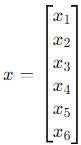 . The equation becomes:
. The equation becomes: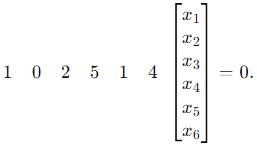
This gives a single linear equation: 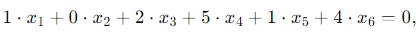
or: x1 + 2x3 + 5x4 + x5 + 4x6 = 0. . ..(1)
Step 2: Parametrize the Solution
We express x1 in terms of the free variables x3, x4, x5, x6
x1 = −2x3 −5x4 − x5 − 4x6.
Let x2 = t2, x3 = t3, x4 = t4, x5 = t5, x6 = t6 , where t2, t3, t4, t5 ,t6 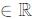 are free parameters.
are free parameters.
Then: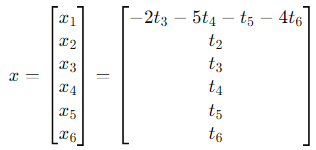
Split this into a linear combination of the free variables: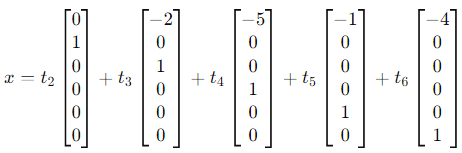
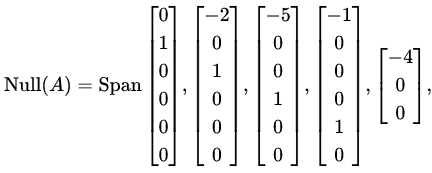
Step 3: Basis for the Null Space
The null space of A is spanned by the vectors:
Question 17. Let V be the vector of all n × n matrices over the fieldof real numbers. A subset W of V is not a subspace of V if W consists of all matrices for which
1. A2 = A
2. A2 ≠ A
3. A = AT
4. A = −AT
Sol:
We are tasked with determining which of the given subsets W of the vector space V (all n × n matrices over the field of real numbers) is not a subspace of V.
Definition of a Subspace:
For W to be a subspace of V, it must satisfy:
1. W is non-empty (contains the zero matrix).
2. W is closed under matrix addition: If A, B ∈ W, then A + B ∈ W.
3. W is closed under scalar multiplication: If A ∈ W and c ∈ R, then c A ∈ W.
Analyzing Each Case:
1. W = A ∈ V : A2 = A (Idempotent Matrices)
- A2 = A implies that A satisfies the quadratic equation A(A − I) = 0, where I is the identity matrix.
- The zero matrix is in W, and it is closed under addition and scalar multiplication:
If A, B ∈ W, then (A + B)2 = (A + B) does not necessarily hold because cross-terms like AB or BA might not satisfy the idempotent condition. - Conclusion: W is not closed under addition, so it is not a subspace.
2. W = A ∈ V : A2 ≠ A
- This subset consists of matrices that do not satisfy A2 = A.
- The subset is not closed under addition or scalar multiplication because combining two matrices A and B in W could result in a matrix A + B for which (A + B)2 = A + B, violating the condition.
- Conclusion: W is not closed under addition or scalar multiplication, so it is not a subspace.
3. W = A ∈ V : A ≠ AT (Symmetric Matrices)
A=A T means A is symmetric.
The zero matrix is symmetric, and the set is closed under addition and scalar multiplication:
- If A, B ∈ W, then (A + B)T = AT + BT = A + B, so A + B ∈ W.
- If c ∈ R and A ∈ W, then (cA)T = cAT = cAT, so c A ∈ W.
Conclusion: W is a subspace.
4. W = A ∈ V : A = - AT ( (Skew-Symmetric Matrices):
- A = −AT means A is skew-symmetric.
- The zero matrix is skew-symmetric, and the set is closed under addition and scalar multiplication:
If A, B ∈ W, then(A + B)T = AT + BT = −A −B = −(A + B), so A + B ∈ W.
If c ∈ R and A ∈ W, then (cA)T = cAT =−cA, so cA ∈ W. - Conclusion: W is a subspace.
Final Answer:
The subset W is not a subspace of V if it consists of matrices satisfying:
A2 = A or A2 ≠ A.
Question 18. Let A be a 4 × 4 invertible matrix. Which of the following is NOT true?
1. The rows of A form a basis of
2. Null space of A contains only the zero vector
3. A has four distinct eigenvalues
4. Image of the linear transformation x → Ax on
Sol:
Let A be a 4 × 4 invertible matrix. We need to determine which of the given statements is NOT true.
Statement 1: The rows of A form a basis of  .
.
- Since A is invertible, its rank is 4, meaning its rows are linearly independent.
- Linearly independent rows of a 4 × 4 matrix span
 .
. - This statement is true.
Statement 2: The null space of A contains only the zero vector.
- For an invertible matrix A, the null space contains only the zero vector because Ax = 0 implies x = 0.
- This statement is true.
Statement 3: A has four distinct eigenvalues.
- An invertible matrix is not guaranteed to have four distinct eigenvalues. The matrix can have repeated eigenvalues, or some eigenvalues may have algebraic multiplicity greater than 1.
- For example, the identity matrix I has a single eigenvalue 1 repeated four times.
- This statement is NOT necessarily true.
Statement 4: The image of the linear transformation x ↦ Ax is  .
.
- Since A is invertible, the transformation x ↦ Ax is surjective, meaning it maps all of
 onto itself.
onto itself. - The image of the transformation is
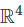 .
. - This statement is true.
Final Answer:
The statement that is NOT true is: A has four distinct eigenvalues.
Question 19. Let Cbe the linear space of all continuous functions from R to R. Let Wc be the set of differentiable functions u(x) that satisfy the differential equation u′ = xu + c. For which value(s) of the real constant c is this set a linear subspace of C (
)?
Sol:
To determine the values of c for which the set Wc is a linear subspace of 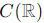 , let's analyze the given conditions and the properties of subspaces.
, let's analyze the given conditions and the properties of subspaces.
Step 1: Definition of Wc
The set Wc is defined as:
Wc = {u(x) ∈ 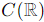 :u ′ (x)=xu(x)+c}.
:u ′ (x)=xu(x)+c}.
Here, u(x) is a differentiable function satisfying the given first-order differential equation.
Step 2: Conditions for Wc to be a Subspace
For Wc to be a subspace of 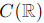 , it must satisfy the following conditions:
, it must satisfy the following conditions:
- Zero function belongs to Wc : The zero function u(x) = 0 must satisfy the differential equation.
- Closed under addition: If u1(x), u2 (x) ∈ Wc , then u1 (x) + u2 (x) ∈ Wc .
- Closed under scalar multiplication: If u(x) ∈ Wc and
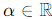 , then αu(x)∈Wc.
, then αu(x)∈Wc.
Step 3: Check the Zero Function
Substitute u(x) = 0 into the differential equation:
u′ (x) = xu(x) + c ⟹ 0 = 0 + c.
For the zero function to satisfy the equation, we require: c = 0.
Step 4: Closure under Addition and Scalar Multiplication
Let u1 (x), u2 (x) ∈ Wc. This means: 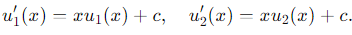
Consider their sum v(x)= u1 (x) + u2 (x). Then: 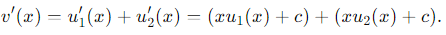
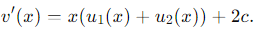
For v(x) to satisfy the differential equation v′ (x) = xv(x) + c, we must have:
2c = c ⟹ c = 0.
Similarly, for scalar multiplication w(x) = αu(x), where 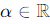 , we find:
, we find:
w′ (x) = αu′ (x) = α(xu(x) + c) = x(αu(x)) + αc.
For w(x) to satisfy w ′ (x) = xw(x) + c, we require:
αc = c ⟹ c(1 − α) = 0.
This holds for all α only if c = 0.
Step 5: Conclusion
The set Wc is a linear subspace of 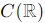 if and only if c = 0.
if and only if c = 0.
Final Answer: c = 0.
Question 20. Let U and V both be two-dimensional subspaces ofand U ≠ V , and let W = U ∩ V . Find all possible values for the dimension of W.
Sol:
We are tasked with finding all possible values for the dimension of W = U∩V, where U and V are two-dimensional subspaces of a vector space 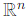 , and U ≠ V.
, and U ≠ V.
Step 1: Key Properties
1. dim (U) = dim (V) = 2 because U and V are two-dimensional subspaces.
2. The dimension of the intersection W = U ∩ V satisfies:
dim (W) ≤ min (dim (U), dim(V)) = 2.
3. The sum of the dimensions of U and V is related to their intersection by the dimension formula:
dim (U + V) = dim (U) + dim (V) − dim (U ∩ V).
Since U + V is a subspace of 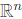 , we know:
, we know:
dim (U + V) ≤ n.
Step 2: Possible Dimensions of W
The intersection W = U ∩ V can have dimension 0, 1, or 2:
1. Case dim(W) = 0: This happens when U and V have no non-zero vectors in common, meaning they are disjoint except for the zero vector.
2. Case dim(W) = 1: This happens when U and V intersect along a one-dimensional subspace (a line through the origin in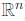 ).
).
3. Case dim (W) = 2: This happens when U = V, which is ruled out by the condition U ≠ V .
Thus, the possible dimensions of W are: d
dim(W) ∈ {0, 1}.
Step 3: Verification
1. For dim(W) = 0:
- If dim(W) = 0, then dim (U + V)dim (U) + dim (V) = 4, provided n ≥ 4.
2. For dim (W) = 1:
- If dim(W) = 1, then dim (U + V)dim (U) + dim (V) - dim (W) = 3, provided n ≥ 3.
Both cases are consistent with the dimension formula and the structure of subspaces in 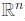 .
.
Final Answer:
The possible dimensions of W = U ∩ V are: dim(W) ∈ {0, 1}.
Question 21. Let Pn be the vector space of all polynomials of degree at most n ≥ 6 with real coefficients. Consider the following subspaces of Pn :
W1 = {p(x) ∈ Pn : p(1) = 0, p(2) = 0, p(3) = 0, p(4) = 0}
W2 = {p(x) ∈ Pn : p(3) = 0, p(4) = 0, p(5) = 0, p(6) = 0}
Find the dimensions of W1, W2 and W1 ∩ W2
Sol:
We are tasked with finding the dimensions of the subspaces W1 , W2 , and W1 ∩ W2 of the vector space Pn , where Pn is the vector space of all polynomials of degree at most n ≥ 6 with real coefficients.
Step 1: Vector Space of Polynomials Pn
The vector space Pn has dimension n + 1, as a general polynomial of degree at most n is written as: 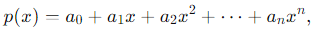
which involves n + 1 coefficients (a0, a1 ,…, an).
Step 2: Subspace W1
The subspace W1 is defined as: 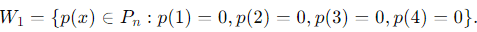
This means that the polynomial p(x) has roots at x = 1, 2, 3, 4. Hence, p(x) must be divisible by:
(x−1)(x−2)(x−3)(x−4).
Since p(x) is a polynomial in Pn , it can be written as:
p(x) = (x−1)(x−2)(x−3)(x−4)q(x),
where q(x) is a polynomial of degree at most n−4.
Thus, the dimension of W1 is the number of free coefficients in q(x), which is:
dim(W1) = (n − 4) + 1 = n − 3.
Step 3: Subspace W2
The subspace W2 is defined as: 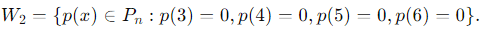
This means that the polynomial p(x) has roots at x = 3, 4, 5, 6. Hence, p(x) must be divisible by:
(x−3)(x−4)(x−5)(x−6).
Similarly, p(x) can be written as:
p(x) = (x−3)(x−4)(x−5)(x−6)q(x),
where q(x) is a polynomial of degree at most n − 4.
Thus, the dimension of W2 is:
dim(W2) = (n − 4) + 1 = n − 3.
Step 4: Intersection W1 ∩W2
The subspace W1 ∩ W2 contains polynomials p(x) that satisfy both W1 and W2.
Such polynomials have roots at: x = 1, 2, 3, 4, 5, 6.
Thus, p(x) must be divisible by:
(x−1)(x−2)(x−3)(x−4)(x−5)(x−6).
Write p(x) as:
p(x)=(x−1)(x−2)(x−3)(x−4)(x−5)(x−6)q(x),
where q(x) is a polynomial of degree at most n−6.
The dimension of W1 ∩W2 is
dim(W1 ∩W2) = (n−6)+1=n−5.
Final Answers:
1. dim(W1)= n − 3,
2. dim(W2) = n − 3,
3. dim(W1 ∩ W2) = n − 5.
Question 22. Let P3 denote the real vector space of all polynomials with real coefficients having degree less than or equal to 3, equipped with the standard ordered basis {1, x, x2 , x3 }. Write down the matrix, w.r.t this basis,of the fol lowing linear transformation:
L(p) = p′′ − 2p′ + p, p ∈ P3
Also, find the unique polynomial p such that L(p) = x3.
Solution. Here,
Thus matrix of L =
Now let p = ax3 + bx2 + cx + d ∈ P3 be such the L(p) = x3 . Then, using the definition of L and equating the coefficients on both sides, we get p = x3 + 6x2 + 18x + 24.
Question 23. A non-zero matrix A ∈ Mn(R) is said to be nilpotent if Ak = 0 for some positive integer k ≥ 2. If A is nilpotent, which of the fol lowing statements are true? 1. k ≤ n for the smal lest such k. 2. The matrix I + A is invertible. 3. Al l the eigenvalues of A are zero.
Sol:
We are tasked with analyzing the properties of a nilpotent matrix 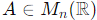 . A matrix A is said to be nilpotent if Ak = 0 for some positive integer k ≥ 2. Let’s examine the given statements:
. A matrix A is said to be nilpotent if Ak = 0 for some positive integer k ≥ 2. Let’s examine the given statements:
Statement 1: k ≤ n for the smallest such k.
Explanation:
- The minimal polynomial of A, which divides the characteristic polynomial, determines the smallest integer k such that Ak = 0
- A k =0.
- The degree of the minimal polynomial cannot exceed n, the size of the matrix A. Hence, the smallest k such that Ak = 0 satisfies k ≤ n.
Conclusion:
This statement is true.
Statement 2: The matrix I + A is invertible.
Explanation:
- If A is nilpotent, then Ak = 0 for some k ≥ 2.
- The matrix I + A can be inverted using the formula for a Neumann series:
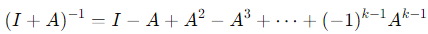
- Since Ak = 0, the series terminates at Ak−1 , ensuring that I + A is invertible.
Conclusion:
- This statement is true.
Statement 3: All the eigenvalues of A are zero.
Explanation:
- If λ is an eigenvalue of A, then there exists a nonzero vector v such that Av = λv.
- Applying Ak = 0 to this eigenvector:
- Akv = λkv = 0.
- Since v ≠ 0 , we conclude that λk = 0, implying λ = 0.
Conclusion:
- This statement is true.
Final Answer:
All three statements are true:
1 , 2 , and 3 are true.
Question 24. Justify whether the fol lowing are true or false:
1. There exist n × n matrices A and B such that AB − BA = I .
2. Let A and B be two arbitrary n × n matrices. If B is invertible, then tr(A) = tr−1 (B − 1AB) where tr(M ) denotes the trace of an n × n matrix M.
Sol:
Statement 1: There exist n × n matrices A and B such that AB − BA = I.
Analysis:
1. The matrix AB − BA (called the commutator of A and B) is always traceless, meaning tr(AB − BA) = 0.
- This is because the trace operator satisfies tr tr(AB) = tr(BA) for any n × n matrices A and B.
- Thus: tr(AB−BA)=tr(AB)−tr(BA)=0.
2. The identity matrix I has tr(I)=n, which is nonzero for any n ≥ 1.
3. Since AB − BA is traceless, it is impossible for AB − BA = I, as their traces would contradict.
Conclusion:
The statement is false.
Statement 2: Let A and B be two arbitrary n × n matrices. If B is invertible, then tr(A) = tr(B −1 AB), where tr(M) denotes the trace of an n × n matrix M.
Analysis:
1. For any n × n matrices A and B, the trace operator satisfies the cyclic property: 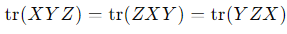
where X,Y,Z are n × n matrices.
2. Apply this property to tr(B −1 AB):
tr(B −1 AB)=tr((AB)B −1)=tr(A(BB −1))=tr(A⋅I)= tr(A).
Hence, the equation tr(A) = tr(B −1 AB) is always true when B is invertible.
Conclusion:
The statement is true.
Final Answer:
1. False: There do not exist n×n matrices A and B such that AB−BA=I.
2. True: If B is invertible, then tr(A)=tr(B −1 AB).
Question 25. Let V be the real vector space of all polynomials in one variable with real coefficients and of degree less than, or equal to 5. Let W be the subspace defined by W = {p ∈ V |p(1) = p′(2) = 0}. What is the dimension of W ?
Sol:
We are tasked with finding the dimension of the subspace W of the real vector space V of polynomials of degree at most 5, where:
V = {p(x) ∣ deg(p(x)) ≤ 5},
and:
W={p(x)∈V∣p(1)=0 and p ′ (2)=0}.
Step 1: Dimension of V
The vector space V consists of all polynomials of degree at most 5. A basis for V is 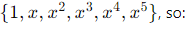
dim(V) = 6.
Step 2: Conditions Defining W
1. Condition 1: p(1) = 0:
- This implies that (x−1) is a factor of p(x).
- Thus, p(x) can be written as:
p(x) =(x−1)q(x),
where q(x) is a polynomial of degree at most 4 (since deg (p(x))≤5).
This condition reduces the dimension of V by 1, so the subspace of polynomials satisfying p(1) = 0 has:
dim=6−1=5.
2. Condition 2: p ′ (2) = 0:
- Differentiate p(x):
p(x)=(x−1)q(x)⟹p ′ (x)=(x−1)q ′ (x)+q(x). - Substitute x = 2 into p′ (x) = 0:
p ′ (2)=(2−1)q ′ (2)+q(2)=q ′ (2)+q(2)=0. - This imposes a linear constraint on the coefficients of q(x).
Since q(x) is a polynomial of degree at most 4, it has 5 coefficients. Imposing q′(2)+q(2)=0 reduces the dimension by 1.
Step 3: Dimension of W
Starting from dim(V) = 6, the two conditions reduce the dimension as follows:
1. p(1) = 0 reduces the dimension by 1 ( dim = 5 dim=5).
2. p ′ (2)=0 reduces the dimension by 1 ( dim = 4 dim=4).
Thus, the dimension of W is: dim(W) = 4.
FAQs on Questions: Linear Algebra and Matrices - Mathematical Methods of Physics, UGC - NET Physics - Physics for IIT JAM, UGC - NET, CSIR NET
| 1. What are the basic concepts of linear algebra that are essential for UGC - NET Physics preparation? |  |
| 2. How do matrices play a role in solving physical problems in UGC - NET Physics? |  |
| 3. What is the significance of eigenvalues and eigenvectors in physics? |  |
| 4. Can you explain the concept of linear independence and its importance in physics? |  |
| 5. How can one effectively study linear algebra for the UGC - NET Physics exam? |  |

















