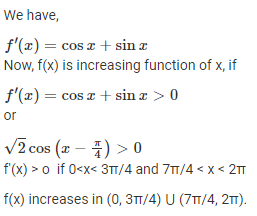Monotonic Functions - Real Analysis, CSIR-NET Mathematical Sciences | Mathematics for IIT JAM, GATE, CSIR NET, UGC NET PDF Download
Monotonic Function - Definition
A monotonic function is a function which is either entirely non-increasing or non-decreasing. A function is monotonic if its first derivative (which need not be continuous) does not change sign.
- The term monotonic may also be used to describe set functions that map subsets of the domain to non-decreasing values of the co-domain.
- In particular, if f: X→Y is a set function from a collection of sets X to an ordered set Y, then f is said to be monotone if whenever A⊂B as elements of X, f(A)≤f(B).
- This particular definition comes up frequently in measure theory where many of the families of functions defined (including outer measure, premeasure, and measure) begin by considering monotonic set functions.
Increasing and Decreasing Function - Definition
Increasing Function - Let y=f(x) be a differentiable function on an interval (a,b). If for any two points x1,x2∈(a,b)such that x1<x2, there holds the inequality f(x1)≤f(x2), the function is called increasing (or non-decreasing) in this interval. If this inequality is strict, i.e. f(x1)<f(x2), then the function y=f(x) is said to be strictly increasing on the interval (a,b).
Decreasing function - Similarly, we define a decreasing (or non-increasing) and a strictly decreasing function.
Example - f(x) = 2x + 3, f(x) = log(x), f(x) = ex are the examples of increasing function and f(x) = -x5 and f(x) = e-x are the examples of decreasing function.
These concepts can be formulated in a more compact form. A function y=f(x) is called
- increasing (non-decreasing) on the interval (a,b) if
∀x1,x2∈(a,b):x1<x2⇒f(x1)≤f(x2);
- strictly increasing on the interval (a,b) if
∀x1,x2∈(a,b):x1<x2⇒f(x1)<f(x2);
- decreasing (non-increasing) on the interval (a,b) if
∀x1,x2∈(a,b):x1<x2⇒f(x1)≥f(x2);
- strictly decreasing on the interval (a,b) if
∀x1,x2∈(a,b):x1<x2⇒f(x1)>f(x2).
It is clear that a non-decreasing function can contain strictly increasing intervals and intervals where the function is constant. This is schematically illustrated in Figures 1−4.




Important - If a function f(x) is differentiable on the interval (a,b) and belongs to one of the four considered types (i.e. it is increasing, strictly increasing, decreasing, or strictly decreasing), this function is called monotonic on this interval.
The concept of increasing and decreasing functions can also be defined for a single point x0. In this case, we consider a small δ-neighborhood (x0−δ,x0+δ) of this point. A function y=f(x) is strictly increasing at x0 if there exists a number δ>0 such that
- ∀x∈(x0−δ,x0)⇒f(x)<f(x0);
- ∀x∈(x0,x0+δ)⇒f(x)>f(x0).
Similarly, we can define a function y=f(x), which is strictly decreasing at the point x0.
Criteria for Increasing and Decreasing Functions
Again consider a function y=f(x) assuming it is differentiable on an interval (a,b). To determine if the function is increasing or decreasing on the interval, we use the sign of the first derivative of the function.
Theorem 1
In order for the function y=f(x) to be increasing on the interval (a,b), it is necessary and sufficient that the first derivative of the function be non-negative everywhere in this interval:
f′(x)≥0∀x∈(a,b).
A similar criterion applies to the case of a function that is decreasing on the interval (a,b):
f′(x)≤0∀x∈(a,b).
We prove both (necessary and sufficient) parts of the theorem for the case of an increasing function.
Necessary condition
Consider an arbitrary point x0∈(a,b). If the function y=f(x) is increasing on (a,b), then by definition, we can write:
- ∀x∈(a,b):x>x0⇒f(x)>f(x0);
- ∀x∈(a,b):x<x0⇒f(x)<f(x0).
It can be seen that in both cases the following inequality holds:

In the limit as x→x0, the left-hand side of the inequality is equal to the derivative of the function at the point x0, that is by the limit sign preservation property:

This relation is valid for any x0∈(a,b).
- Consider the sufficient condition, i.e. the converse statement. Suppose that the derivative f′(x) of a function y=f(x) is non-negative in the interval (a,b): f′(x0)≥0∀x∈(a,b).
- If x1 and x2 are two arbitrary points of the interval such that x1<x2, then by Lagrange’s theoremwe can write: f(x2)−f(x1)=f′(c)(x2−x1),where c∈[x1,x2], ⇒c∈(a,b).
- Since f′(c)≥0, then the right-hand side of the equality is non-negative. Consequently,
- f(x2)≥f(x1). i.e. the function y=f(x) is increasing in the interval (a,b).
Consider now the cases of a strictly increasing and strictly decreasing function. There exists a similar theorem that describes the necessary and sufficient conditions. Omitting the proof, we state it for the case of a strictly increasing function.
Theorem 2
Suppose that a function y=f(x) is differentiable on an interval (a,b). In order for the function to be strictly increasing in this interval, it is necessary and sufficient that the following conditions are satisfied:
1. f′(x)≥0∀x∈(a,b);
2. f′(x) is not identically equal to zero at any interval [x1,x2]∈(a,b).
- Condition 1 is contained in Theorem 1 and is an indication of a non-decreasing function.
- The additional condition 2 is required in order to exclude the intervals of constancy, in which the derivative of f(x) is identically zero.
- In practice (when finding the intervals of monotonicity), the sufficient condition for a strictly increasing or a strictly decreasing function is commonly used.
- Theorem 2 implies the following wording of the sufficient criterion: If the condition f′(x)>0 is satisfied for all x∈(a,b), except perhaps only a few distinct points where f′(x)=0, then the function f(x) is strictly increasing in this interval.
- Accordingly, the condition f′(x)<0 defines a strictly decreasing function.
- The number of points where f′(x)=0 is usually finite.
- According to Theorem 2, they can not tightly fill any subinterval of the interval (a,b).
We also give a criterion for increasing/decreasing functions at a point:
Theorem 3
Let x0∈(a,b).
- If f′(x0)>0, then the function f(x) is strictly increasing at the point x0;
- If f′(x0)<0, then the function f(x) is strictly decreasing at the point x0.
Examples of Increasing and Decreasing Graphs
Example - 1
Consider the following two graphs. The red one is f(x)=3x while the green one is g(x)=3x+1: Notice that as x is increasing, f(x) is increasing. Now notice this algebraic manipulation:
Notice that as x is increasing, f(x) is increasing. Now notice this algebraic manipulation:
g(x)=3x+1=3⋅3x=3f(x)
Therefore, g(x) is also monotonically increasing. You can multiply f(x) by any positive constant, and the values of the new function will continue to grow at a faster or slower rate as x increases.
Example - 2
Now we consider a logarithmic function.
We will use an example involving the common logarithm. Let f(x)=log10(x). A graph is shown below:
 The graph is curved upward where the function is defined (positive real numbers), in a way that it is always increasing. Any logarithm with a positive base will have a similar pattern.
The graph is curved upward where the function is defined (positive real numbers), in a way that it is always increasing. Any logarithm with a positive base will have a similar pattern.
Example - 3
Consider the graph of f(x)=−5x, shown below:
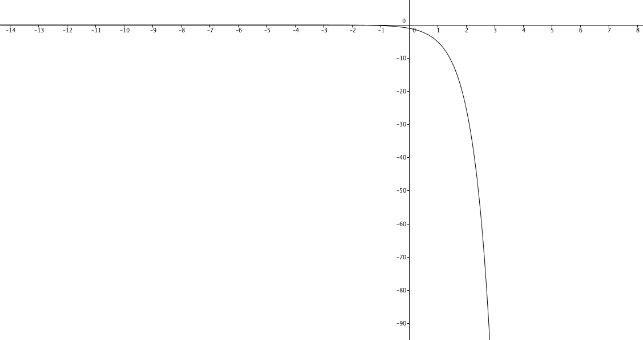 The function 5x is monotonically increasing, so f(x)=−5x must be monotonically decreasing, because wherever 5x is increasing (everywhere), f(x) is decreasing.
The function 5x is monotonically increasing, so f(x)=−5x must be monotonically decreasing, because wherever 5x is increasing (everywhere), f(x) is decreasing.
Properties of Monotonic Functions
Increasing and decreasing functions have certain algebraic properties, which may be useful in the investigation of functions. Here are some of them
1. If the functions f and g are increasing (decreasing) on the interval (a,b), then the sum of the functions f+g is also increasing (decreasing) on this interval
2. If the function f is increasing (decreasing) on the interval (a,b), then the opposite function −f is decreasing (increasing) on this interval.
3. If the function f is increasing (decreasing) on the interval (a,b), then the inverse function 1\f is decreasing (increasing) on this interval.
4. If the functions f and g are increasing (decreasing) on the interval (a,b) and moreover, f≥0, g≥0, then the product of the functions fg is also increasing (decreasing) on this interval.
5. If the function g is increasing (decreasing) on the interval (a,b) and the function f is increasing (decreasing) on (c,d) where g:(a,b)→(c,d), then the composition of functions f∘g
(i.e. the composite function y=f(g(x)) is also increasing (decreasing) on the interval (a,b).
Non monotonic Function
The functions which are increasing as well as decreasing in their domain are known as non monotonic function.
Example: f(x) = sin x , f(x) = |x| are examples of non monotonic function. But f(x) = sin x is increasing in [0, Π/2] or we can say it is monotonic in [0, Π/2].
Questions
Q.1. What is the difference between monotonically increasing and strictly increasing?
Ans. A function that is monotonically increasing is always increasing on its domain; a condition of this is to have the derivative of the function being greater than or equal to zero. A function is strictly monotonically increasing if it is always increasing on its domain and its graph is never horizontal; that is, the derivative of the function is strictly greater than zero on its domain.
Q.2. What is the meaning of monotonic function?
Ans. A monotonic function is a function that is either always increasing or always decreasing on its domain. To check if a function is monotonic, find its derivative and see if it is greater than or equal to zero (monotonically increasing) or lesser than or equal to zero (monotonically decreasing).
Q.3. How do you tell if a function is monotonically increasing?
Ans. To tell if a function is monotonically increasing, simply find its derivative and see if it is always positive on its domain. If the derivative of a function is always positive (or greater than or equal to zero), then the function is monotonically increasing.
Q.4. What is meant by monotonically increasing?
Ans. A monotonically increasing function is a function that is always increasing on its domain. That is, for any two values a,b such that a<b, the function f outputs f(a) < f(b). Or, the derivative of a function f is always positive also means the function is always increasing.
Q.5. Prove that f(x) = x – sin(x) is an increasing function.
Ans. f(x) = x – sin(x)
⇒ dy/dx = 1 – cos(x)
dy/dx ≥ 0 as cos(x) having value in interval [-1,1] and dy/dx = 0 for the discrete values of x and do not form an interval, hence we can include this function in monotonically increasing function.
Q.6. In what interval is the function sin x – cos x increasing?
Ans.
|
556 videos|198 docs
|
FAQs on Monotonic Functions - Real Analysis, CSIR-NET Mathematical Sciences - Mathematics for IIT JAM, GATE, CSIR NET, UGC NET
| 1. What is the definition of a monotonic function? |  |
| 2. How is an increasing and decreasing function defined? |  |
| 3. What are the criteria for determining if a function is increasing or decreasing? |  |
| 4. Can you provide examples of graphs of increasing and decreasing functions? |  |
| 5. What are some properties of monotonic functions? |  |
|
556 videos|198 docs
|

|
Explore Courses for Mathematics exam
|

|