Sturm-Liouville Boundary Value Problem - CSIR-NET Mathematical Sciences | Mathematics for IIT JAM, GATE, CSIR NET, UGC NET PDF Download
SL equation
A classical ”’Sturm-Liouville equation”’, is a real second-order linear differential equation of the form
 (1)
(1)
In the simplest of cases all coefficients are continuous on the finite closed interval [a, b], and p(x) has continuous derivative. In this case y is called a ”solution” if it is continuously differentiable on (a, b) and satisfies the equation (1) at every point in (a, b). In addition, the unknown function y is required to satisfy boundary conditions. The function r(x), is called the ”weight” or ”density” function.
The number of “famous” differential equations could be represented in the SL form:
- Bessel’s equation
x2 y" + xy' + (x2 − ν2)y = 0
can be written in Sturm-Liouville form as
(xy')' + (x − ν2/x)y = 0.
- The Legendre equation:
(1 − x2)y" − 2xy' + ν (ν + 1)y = 0
can easily be put into SL form, since (1 − x2)' = −2x, so, the Legendre equation is equivalent to
[(1 − x2)y']' + ν (ν + 1)y = 0
The general way to convert the 2nd order linear ODE to the SL form is to use an integrating factor µ(x) such that the equation
P (x)y" + Q(x)y' + R(x)y = 0
multiplied by µ(x) would have the SP form. One cane easily show that does the job.

SL Boundary Value Problem (SL-BVP)
We introduce the SL-operator as

and consider the SL equation
 (2)
(2)
where  and p, q and r are continuous functions on the interval [a, b]; along the with BC
and p, q and r are continuous functions on the interval [a, b]; along the with BC

 (3)
(3)
where 
The problem of finding a complex number λ = µ such that the BVP (2)-(3) has a non-trivial solution is called SLP.
The value λ = µ is called an eigenvalue and the corresponding solution y(:, µ) is called an eigenfunction
There are three types of SLP:
1. A SLP is called regular if p > 0, and r > 0 on [a, b]
2. A SLP is called singular if p > 0 on (a, b), r ≥ 0 on [a, b] and p(a) = p(b) = 0.
3. A SLP is called periodic if p > 0, r > 0 and p, q and r are continuous functions on [a, b]; along with the following BC:
y(a) = y(b) y' (a) = y' (b) .
The most common types of SLP are regular and periodic, which will be discussed in more detail.
Example 1
For λ ∈ R solve
y" + λy = 0, y(0) = y' (π) = 0
We consider three cases corresponding to values of λ:
- λ = −µ2 < 0
The general solution of the ODE is given as
y = Ae−µx + Beµx
By substituting BC we obtain the following system:
This system has only trivial solution A = B = 0 (determinant of its matrix of coefficients is different from 0)
- λ = 0
In this case the problem has a solution y = Ax + B and by substituting BC one can check that A = B = 0 (we get a trivial solution as well).
- λ = µ2 > 0
The general solution of the ODE is given as
y = A cos(µx) + B sin(µx)
By substituting BC we obtain the following system:
This problem has non-trivial solution (enabling B ≠ 0) only when cos(µπ) = 0 or µ = (2n − 1)/2. Therefore the eigenvalues λn could be written a
and the eigenfunctions (we choose Bn = 1) are
Note that all the eigenvalues λn are positive and the eigenfunctions corresponding to each eigenvalue form a one dimensional vector space, and so the eigenfunctions are unique up to a constant multiple
Example 2
For λ ∈ R solve
y" + λy = 0, y(0) − y(π) = 0, y' (0) − y' (π) = 0
These BC are called “periodic BC”.
We consider three cases corresponding to values of λ:
- λ = −µ2 < 0
The general solution of the ODE is given as
y = Ae−µx + Beµx
By substituting BC we obtain the following system:
This system has only trivial solution A = B = 0 (for µ ≠ 0)
- λ = 0
In this case the problem has a solution y = Ax + B and by substituting BC we obtain A = 0 and B is an arbitrary constant. This corresponds to the eigenvalue λ0 = 0 and the eigenfunction (we set B = 1).Note that this eigenvalue is simple. The eigenvalue is called simple, if its eigenspace is of dimension one; otherwise the eigenvalue is called multiple.
(we set B = 1).Note that this eigenvalue is simple. The eigenvalue is called simple, if its eigenspace is of dimension one; otherwise the eigenvalue is called multiple.
- λ = µ2 > 0
The general solution of the ODE is given as
y = A cos(µx) + B sin(µx)
By substituting BC we obtain the following system:
This problem has a non-trivial solution only when the determinant of the matrix of coefficients D(µ) = 2 − cos(µπ) = 0. This corresponds to µ = 2n, n = ±1, ±2, ... and hence λn = 4n2.
The eigenfunctions corresponding to λn are given by (A = B = 1)
Note that all the eigenvalues λn are positive and there are two linearly independent eigenfunctions corresponding to each eigenvalue, so they are not unique.
Regular SLP
Properties:
1. The eigenvalues of the regular SLP are real
PROOF: Suppose λ ∈ C is an eigenvalue of the regular SLP and let y be corresponding eigenfunction. That is,
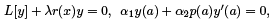
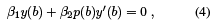
Taking the complex conjugates we get


Multiplying the ODE in 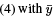 and the ODE in (5) with y and subtracting one from another yields
and the ODE in (5) with y and subtracting one from another yields
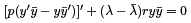
Integrating the last expression we obtain
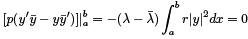
The LHS of the last identity is zero due to the BC. Thus we have
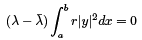
From the definition of regular SLP we know that r > 0 and y as an eigenfunction is different from zero as well. Therefore the only way to satisfy the identity is to set 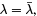 which means that λ is real.
which means that λ is real.
2. The eigenfunctions of a regular SLP corresponding to the distinct eigenvalues are orthogonal w.r.t. the weight function r(x) on [a, b]. By other words, if the eigenfunctions u and v correspond to the distinct eigenvalues λ and µ then
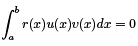
PROOF: As in the previous case we write the SL equations for functions u and v, multiply one for u by v and vice versa and subtract one equation from another. As result we get

Integrating the last expression we obtain
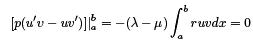
The LHS of the last identity is zero due to the BC. Thus we have
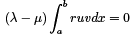
We know that λ = µ therefore 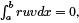 which confirms orthogonality.
which confirms orthogonality.
3. The eigenvalues of the regular SLP are simple. Thus an eigenfunction that corresponds to an eigenvalue is unique up to a constant multiple.
4. The regular SL operator L is self-adjoint: if whenever  and satisfy the regular SLP and BC then
and satisfy the regular SLP and BC then

PROOF:


By symmetry we see that


Subtracting one expression from another and applying BC Ba [u] = Ba [v] = Bb [u] = Bb [v] = 0 we obtain:

Theorem: A self-adjoint regular SLP has an infinite number of real eigenvalues λn that are simple and satisfying
λ1 < λ2 < ... < λn < ...
with limn→∞ λn = ∞
Periodic SLP
Properties:
1. The eigenvalues (if any) of the periodic SLP are real
2. The eigenfunctions of a periodic SLP corresponding to the distinct eigenvalues are orthogonal w.r.t. the weight function r(x) on [a, b]. By other words, if the eigenfunctions u and v correspond to the distinct eigenvalues λ and µ then
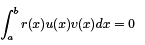
3. The eigenvalues of the regular SLP are not simple. Thus an eigenfunction that corresponds to an eigenvalue is not unique.
4. The periodic SL operator L is self-adjoint
All the proofs for periodic SLP are similar to the regular SLP and rely on the BC.
Theorem: A self-adjoint periodic SLP has an infinite number of real eigenvalues λn satisfying
−∞ < λ1 < λ2 ≤ λ3 ≤ ... ≤ λn ≤ ...
The first eigenvalue λ1 is simple. The number of linearly independent eigenfunctions corresponding to any eigenvalue λn = µ (n > 1) is equal to the number of times µ is repeated in the above listing.
Representation of solutions and numerical calculation
The SL equation with boundary conditions may be solved in practice by a variety of numerical methods. In difficult cases, one may need to carry out the intermediate calculations to several hundred decimal places of accuracy in order to obtain the eigenvalues correctly to a few decimal places.
There are the most common methods used for this purpose:
- Shooting methods. These methods proceed by guessing a value of λ, solving an initial value problem defined by the boundary conditions at one endpoint, say, a, of the interval [a, b], comparing the value this solution takes at the other endpoint b with the other desired boundary condition, and finally increasing or decreasing λ as necessary to correct the original value. This strategy is not applicable for locating complex eigenvalues.
- Finite difference method. The method involves approximation of SL on the small sub-intervals of [a, b] using the first few terms of Taylor series expansion of y.
- The Spectral Parameter Power Series (SPPS) method. It makes use of a generalization of the following fact about second order ordinary differential equations: if y is a solution which does not vanish at any point of [a, b], then the function

is a solution of the same equation and is linearly independent from y. Further, all solutions are linear combinations of these two solutions. In the SPPS algorithm, one must begin with an arbitrary value λ∗0 (often λ∗0 = 0; it does not need to be an eigenvalue) and any solution y0 of SLP with λ = λ∗0 which does not vanish on [a, b].
Two sequences of functions referred to as ”iterated integrals”, are defined recursively as follows. First when n = 0, they are taken to be identically equal to 1 on [a, b]. To obtain the next functions they are multiplied alternately by
referred to as ”iterated integrals”, are defined recursively as follows. First when n = 0, they are taken to be identically equal to 1 on [a, b]. To obtain the next functions they are multiplied alternately by  and integrated, specifically
and integrated, specifically
when n > 0. The resulting iterated integrals are now applied as coefficients in the following two power series in λ:
Then for any λ (real or complex), u0 and u1 are linearly independent solutions of the corresponding SL equation. (The functions p(x) and q(x) take part in this construction through their influence on the choice of y0)
Next one chooses coefficients c0 and c1 so the combination y = c0 u0 +c1 u1 satisfies the first boundary condition Ba [y]. This is simple to do The values of
The values of  provide the values of u0 (b) and u1 (b) and the derivatives
provide the values of u0 (b) and u1 (b) and the derivatives  so the second boundary condition Bb [y] becomes an equation in a power series in λ. For numerical work one may truncate this series to a finite number of terms, producing a calculable polynomial in λ whose roots are approximations of the sought-after eigenvalues. The SPPS method can, itself, be used to find a starting solution y0.
so the second boundary condition Bb [y] becomes an equation in a power series in λ. For numerical work one may truncate this series to a finite number of terms, producing a calculable polynomial in λ whose roots are approximations of the sought-after eigenvalues. The SPPS method can, itself, be used to find a starting solution y0.
|
556 videos|198 docs
|
FAQs on Sturm-Liouville Boundary Value Problem - CSIR-NET Mathematical Sciences - Mathematics for IIT JAM, GATE, CSIR NET, UGC NET
| 1. What is a Sturm-Liouville boundary value problem? |  |
| 2. How is a Sturm-Liouville boundary value problem solved? |  |
| 3. What are the applications of Sturm-Liouville boundary value problems? |  |
| 4. Are Sturm-Liouville boundary value problems only applicable to linear differential equations? |  |
| 5. Can Sturm-Liouville boundary value problems have multiple sets of eigenvalues and eigenfunctions? |  |
|
556 videos|198 docs
|

|
Explore Courses for Mathematics exam
|

|
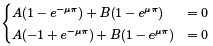
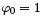 (we set B = 1).Note that this eigenvalue is simple. The eigenvalue is called simple, if its eigenspace is of dimension one; otherwise the eigenvalue is called multiple.
(we set B = 1).Note that this eigenvalue is simple. The eigenvalue is called simple, if its eigenspace is of dimension one; otherwise the eigenvalue is called multiple.
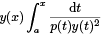
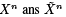 referred to as ”iterated integrals”, are defined recursively as follows. First when n = 0, they are taken to be identically equal to 1 on [a, b]. To obtain the next functions they are multiplied alternately by
referred to as ”iterated integrals”, are defined recursively as follows. First when n = 0, they are taken to be identically equal to 1 on [a, b]. To obtain the next functions they are multiplied alternately by 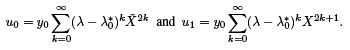
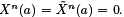 The values of
The values of 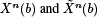 provide the values of u0 (b) and u1 (b) and the derivatives
provide the values of u0 (b) and u1 (b) and the derivatives 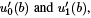 so the second boundary condition Bb [y] becomes an equation in a power series in λ. For numerical work one may truncate this series to a finite number of terms, producing a calculable polynomial in λ whose roots are approximations of the sought-after eigenvalues. The SPPS method can, itself, be used to find a starting solution y0.
so the second boundary condition Bb [y] becomes an equation in a power series in λ. For numerical work one may truncate this series to a finite number of terms, producing a calculable polynomial in λ whose roots are approximations of the sought-after eigenvalues. The SPPS method can, itself, be used to find a starting solution y0.

















