Characteristic Numbers and Eigenfunctions - Linear Integral Equations, CSIR-NET Mathematical Science | Mathematics for IIT JAM, GATE, CSIR NET, UGC NET PDF Download
Def. Integral equation. An equation in which the unknown function occurs under an integral sign. Examples of integral equations are Fredholm’s integral equations of the first, second and third kinds:
1. Fredholm’s integral equation of the first kind. The equation
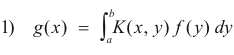
in which g and K are two given functions and f is the unknown function.
2. Fredholm’s integral equation of the second kind. The equation
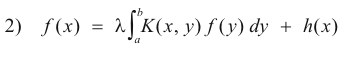
in which h and K are two given functions and f is the unknown function.
3. Fredholm’s integral equation of the third kind. The equation
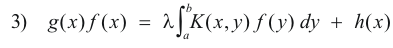
in which g, h and K are given functions and f is the unknown function.
Kernel of an integral equation. The function K(x, y) in the above equations is called the kernel of the equation. If K(x, y) = K(y, x) the kernel is said to be symmetric.
Of special interest is Fredholm’s integral equation of the second kind. Many problems in physics lead to this equation. One place where it arises is in the study of small oscillations of elastic systems.
This equation has two forms, inhomogeneous and homogeneous:
Inhomogeneous form
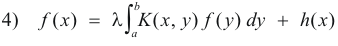
Homogeneous form
The inhomogeneous form corresponds to 2) above and the homogeneous form is obtained from the inhomogeneous form by letting h(x) = 0.
The homogeneous equation always has the zero solution, i.e. the solution y(x) = 0.
In operator notation the inhomogeneous integral equation 4) above can be written as
f = λAf + h
and the homogeneous equation as
f = λAf
where A denotes the operator.
Theorem 1. If Fredholm’s homogeneous integral equation has only the zero solution, then the corresponding inhomogeneous equation is soluble for every function f(x).
Eigenvectors and eigenvalues. Given: a linear operator A on a vector space V. An eigenvector is a nonzero vector v ε V that is imaged by A into a vector λv, a scalar multiple of itself. That is, it is a vector v ε V such that Av = λv where λ is a scalar called an eigenvalue. An eigenvector of a linear operator A corresponds to any of those vectors in the domain which are imaged by A into scalar multiples of themselves.
Eigenvalues and eigenvectors are highly importance in applications. They arise in many areas of mathematics, physics, chemistry and engineering. They arise in analytic geometry in connection with finding that particular coordinate system in which a conic in the plane or a quadric surface in three-dimensional space finds its simplest canonical expression. In physics and engineering they arise in connection with finding, for example, the critical frequencies of a vibrating string, suspension bridge or rotating shaft, the critical load of a supporting column or the energy levels of a system in quantum mechanics.
For the case when the vector space V is n-space and the operator A is an n-square matrix, the eigenvalues are given as the roots of the characteristic equation of matrix A and the eigenvectors are vectors in n-space that A images into scalar multiples of themselves. For the case when A is an integral operator and V is Hilbert space, eigenvectors correspond to those vectors (functions) of Hilbert space that A images into scalar multiples of themselves. In this case the eigenvectors are called eigenfunctions. For example, the homogeneous integral equation
can be written as Af = λf and the solution f(x) of the equation corresponds to those functions that A carries into scalar multiples of themselves.
Many problems in physics lead to homogeneous integral equations in which the kernels are symmetric as a consequence of the law of conservation of energy. The eigenfunctions and eigenvalues of equations with symmetric kernels have a number of important properties. For example:
Theorem 2. A homogeneous integral equation with a symmetric kernel always has a sequence of real eigenvalues
λ1 , λ2, ...... , λn , ......
To every eigenvalue there correspond one or more eigenfunctions. The eigenfunctions corresponding to distinct eigenvalues are always orthogonal to each other.
Example. The problem of finding the characteristic frequencies of a vibrating string of length l, tension t, and density (mass per unit length) ρ, fastened at both ends, leads to the homogeneous integral equation with a symmetric kernel
where
and ω represents frequency.
This equation has the solution u(x) ≡ 0 for every value of ω, which corresponds to the state of rest. The values of ω for which other solutions exist are called the eigenfrequencies of the system.
The system can perform free oscillations only at definite frequencies. The smallest of these is called the fundamental tone of the system and the others are overtones.
Solution of the above equation yields an infinite sequence of eigenfrequencies, the so-called frequency spectrum
ω1 , ω2, ...... , ωn , ......
The nonzero solution un(x) corresponding to the frequency ωn represents the form of the corresponding characteristic oscillation.
The characteristic frequencies are
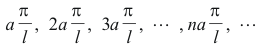
where
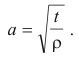
The fundamental tone is ω1 = a(π/l) and the overtones are ω2 = 2ω1, ω3 = 3ω1, ..... , ωn = nω1. The form of the corresponding harmonic oscillations is given by the equation
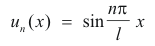
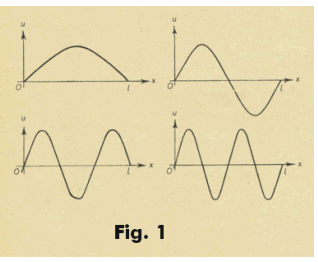
and illustrated in Fig. 1 for n = 1, 2, 3, 4, ....
Self-adjoint linear operators. For an arbitrary linear operator in a Hilbert space the analogue of the symmetric kernel of the integral equation is the property of self-adjointness of the operator. The condition for an operator to be self-adjoint is that for any two elements f1 and f2 of the space the equation
(A f1, f2) = ( f1, Af2)
holds, where (A f1, f2) denotes the inner product of A f1 and f2.
Theorem 3. An integral operator with a symmetric kernel is self-adjoint.
Arbitrary self-adjoint operators have a number of important properties that are useful in applications.
Theorem 4. The eigenvalues of a self-adjoint linear operator are always real and the eigenfunctions corresponding to distinct eigenvalues are orthogonal to each other.
We note the similarity between Theorems 2 and 4.
|
556 videos|198 docs
|
FAQs on Characteristic Numbers and Eigenfunctions - Linear Integral Equations, CSIR-NET Mathematical Science - Mathematics for IIT JAM, GATE, CSIR NET, UGC NET
| 1. What are characteristic numbers and eigenfunctions in the context of linear integral equations? |  |
| 2. How do characteristic numbers and eigenfunctions help in solving linear integral equations? |  |
| 3. Can linear integral equations have multiple sets of characteristic numbers and eigenfunctions? |  |
| 4. How are characteristic numbers and eigenfunctions related to the spectral theory of linear integral equations? |  |
| 5. Are there any applications of characteristic numbers and eigenfunctions in real-world problems? |  |
|
556 videos|198 docs
|

|
Explore Courses for Mathematics exam
|

|

















