Lagrange’s Equations - Classical Mechanics, CSIR-NET Mathematical Sciences | Mathematics for IIT JAM, GATE, CSIR NET, UGC NET PDF Download
Starting with d’Alembert’s principle, we now arrive at one of the most elegant and useful formulations of classical mechanics, generally referred to as Lagrange’s equations. This treatment is taken from Goldstein’s graduate mechanics text, as his treatment seems somewhat more clear to me than Sommerfeld’s.
1.1 Lagrange’s equations from d’Alembert’s principle
We begin with d’Alembert’s principle written in its most fundamental and general form,

where the subscript i ranges over all three components of all particles involved in the system of interest. The first step is to rewrite the particle positions, represented by the xi in groups of three for each particle, in terms of independent generalized coordinates qj . If there are constraints in the system, then there are fewer q variables than x variables. For example, a wheel rotating on a fixed axle has only one q, the angle of rotation, whereas there are three times as many x variables as there are atoms in the wheel.
For holonomic constraints we can write
xi = xi (qj, t) (1.2)
where we allow for the possibility that the relationship between the q and x variables to depend on time.
We can rewrite d’Alembert’s principle by noting that
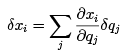 (1.3)
(1.3)
where the time dependence is not exercised since virtual changes are assumed to take place at a fixed time. Thus,
 (1.4)
(1.4)
where the
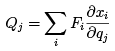 (1.5)
(1.5)
are called the generalized forces. Notice that just as the qi need not have the units of length, the Qi need not have the units of force. However, the product must have the units of energy. For instance, if q is a dimensionless angle, then the corresponding Q would be a torque, which has energy units.
Turning to the inertial forces in d’Alembert’s principle, we note that
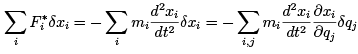 (1.6)
(1.6)
where we have used equation (1.3) in the last step. Using the product rule backwards, we see that
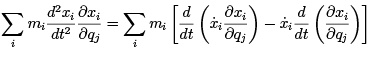 (1.7)
(1.7)
To make further progress, we take the total time derivative of equation (1.2), resulting in
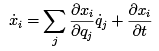 (1.8)
(1.8)
where  are the actual particle velocity components.
are the actual particle velocity components.
We call the 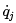 the generalized velocities. Taking the partial derivative of equation (1.8) with respect to a particular qj , we immediately conclude that
the generalized velocities. Taking the partial derivative of equation (1.8) with respect to a particular qj , we immediately conclude that
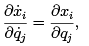 (1.9)
(1.9)
where the derivative of the second term in equation (1.8) is zero because the velocities are not functions of the positions at an instant in time. (Ultimately, the positions can be derived from the velocities by integration, but this relationship depends on knowing the complete time history of the velocities, not just the values at a particular time.)
Finally, we note that
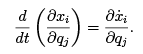 (1.10)
(1.10)
To show this, change the dummy summation index in equation (1.8) from j to k to avoid confusion, and take the partial derivative of this equation with respect to qj :
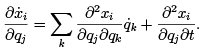 (1.11)
(1.11)
This is possible again because 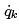 is not an explicit function of the qj. Then compare this with
is not an explicit function of the qj. Then compare this with
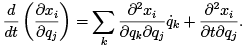 (1.12)
(1.12)
Aside from the order of partial derivatives, the right sides of equations (1.11) and (1.12) are identical, which proves equation (1.10).
Substituting equations (1.9) and (1.10) in equation (1.7) results in
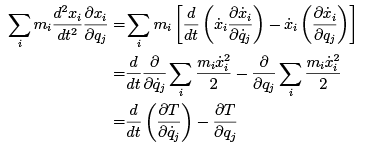 (1.13)
(1.13)
where we recognize the sums as the total kinetic energy T of the system.
Combining equations (1.4), (1.6), and (1.13) yields
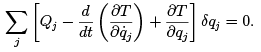 (1.14)
(1.14)
Since the qi are independent of each other, the coefficients of the δqi are individually zero, resulting in Lagrange’s equations:
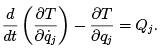 (1.15)
(1.15)
Often forces are conservative and possible to represent as the gradient of a potential energy 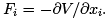 Starting with the definition of generalized forces in equation (1.5), we find that
Starting with the definition of generalized forces in equation (1.5), we find that
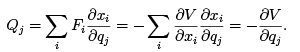 (1.16)
(1.16)
If in addition, V is not an explicit function of time or of the generalized velocities, equation (1.15) may be written
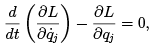 (1.17)
(1.17)
where L = T V is called the Lagrangian. The lack of dependence on time and the generalized velocities allows the V to be incorporated in the first as well as the second terms of this equation. If some of the forces are conservative and others are not, then the more general form may be used.
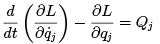 (1.18)
(1.18)
The quantities
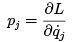 (1.19)
(1.19)
are called the generalized momenta. Note that when the Lagrangian is not a function of a particular generalized coordinate and the associated non-conservative force Qj is zero, then the associated generalized momentum is conserved, since equation (1.18) reduces to
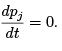 (1.20)
(1.20)
To summarize, these equations are valid for systems obeying the following conditions:
1. The constraints on the system are holonomic, so that the qj are independent for both finite and infinitesimal displacements. The constraints may be time dependent.
2. The potential energy V is a function only of the qj . If there are forces for which no such potential exists, then they can be included on the right side of equation (1.18) in the Qj.
|
556 videos|198 docs
|
FAQs on Lagrange’s Equations - Classical Mechanics, CSIR-NET Mathematical Sciences - Mathematics for IIT JAM, GATE, CSIR NET, UGC NET
| 1. What are Lagrange's equations in classical mechanics? |  |
| 2. How are Lagrange's equations derived? |  |
| 3. What is the significance of Lagrange's equations in classical mechanics? |  |
| 4. How do Lagrange's equations differ from Newton's laws of motion? |  |
| 5. Can Lagrange's equations be used to solve any problem in classical mechanics? |  |
|
556 videos|198 docs
|

|
Explore Courses for Mathematics exam
|

|

















