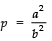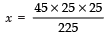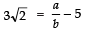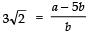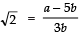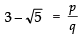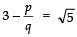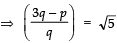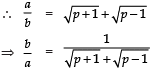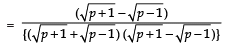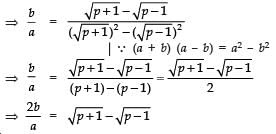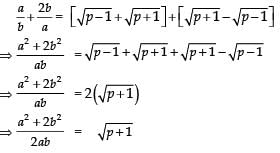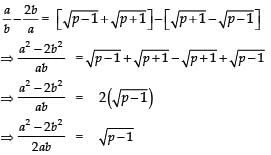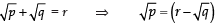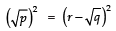Class 10 Maths Chapter 1 Question Answers - Real Numbers - 1

Q1: Prove that √3 is irrational.
Let √3 be rational in the simplest form of P/q.
i.e., p and q are integers having no common factor other than 1 and q ≠ 0.
Now, √3 = p/q
Squaring both sides, we have
⇒ (√3)2 = (p/q)2
⇒ 3 = p2/q2
⇒ 3q2 = p2 ............(1)
Since 3q2 is divisible by 3
∴ p2 is also divisible by 3
⇒ p is divisible by 3 ..........(2)
Let p = 3c for some integer ‘c’.
Substituting p = 3c in (1), we have:
⇒ 3q2 = (3c)2
⇒ 3q2 = 9c2
⇒ q2 = 3c2
3c2 is divisible by 3
∴ q2 is divisible by 3
⇒ q is divisible by 3 ...(3)
From (2) and (3)
3 is a common factor of ‘p’ and ‘q’. But this contradicts our assumption that p and q are having no common factor other than 1.
∴ Our assumption that √3 is rational is wrong.
Thus, √3 is an irrational.
Q2: If ‘p’ is prime, prove that √p is irrational.
Let √p be rational in the simplest form a/b, where p is prime.
∴ a and b are integers having no common factor other than 1 and b ≠ 0.
⇒ Now, √p = a/b
⇒ Squaring both sides, we have
⇒ pb2 = a2 ...(1)
⇒ Since pb2 is divisible by p, a2 is also divisible by p.
⇒ a is also divisible by p ...(2)
Let a = pc for some integer c.
⇒ Substituting a = pc in (1), we have
pb2 = (pc)2
⇒ pb2 = p2c2
⇒ b2 = pc2
pc2 is divisible by p,
∴ b2 is divisible by p
⇒ b is divisible by p ...(3)
From (2) and (3),
⇒ p is a common factor of ‘a’ and ‘b’. But this contradicts our assumption that a and b are co-prime.
∴ Our assumption that √p is rational is wrong. Thus, √p is irrational if p is prime.
Q3: Find the HCF of 18 and 24 using prime factorisation.
Using factor tree method, we have:
∴ 18 = 2 × 3 × 3 = 2 × 32
24 = 2 × 2 × 2 × 3 = 23 × 3
HCF = Product of common prime factors with lowest powers.
⇒ HCF (18, 24) = 3 × 2 = 6
Q4: Find the LCM of 10, 30 and 120.
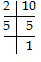

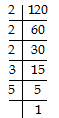
∴ 10 = 2 × 5 = 21 × 51
30 = 2 × 3 × 5 = 21 × 31 × 51
120 = 2 × 2 × 2 × 3 × 5 = 23 × 31 × 51
LCM = Product of each prime factor with highest powers
⇒ LCM of 10, 30 and 120 = 23 × 3 × 5 = 120.
Q5: Find the LCM and HCF of 1296 and 5040 by prime factorisation method.
and
∴ 5040 = 2 × 2 × 2 × 2 × 3 × 3 × 5 × 7
= 24 × 32 × 5 × 7 and
⇒ 1296 = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3
= 24 × 34
∴ LCM = Product of each prime factor with highest powers
= 24 × 34 × 5 × 7
= 16 × 81 × 5 × 7 = 45360
HCF = Product of common prime factors with lowest powers
= 24 × 32
= 16 × 9 = 144
Q6: Show that 3√2 is irrational.
Let 3√2 be a rational number
∴ p/q = 3√2 where p and q are prime to each other and q ≠ 0.
∴ p/3q = √2 ...(1)
Since, p is integer and 3q is also integer (3q≠ 0).
∴ p/3q is a rational number.
From (1), √2 is a rational number.
But this contradicts the fact that √2 is irrational. Therefore, our assumption that 3√2 is rational is incorrect.
Hence, 3√2 is irrational.
Q7: Show that 2 - √3 is an irrational number.
Let 2 - √3 is rational.
∴ It can be expressed as p/q where p and q are integers (prime to each other) such that q ≠ 0.
∴ 2 - √3 = p/q
⇒...(1)
∵ p is an integer}
∴ q is an integer}
⇒ p/q is a rational number.
∴is a rational number. ...(2)
From (1) and (2), √3 is a rational number. This contradicts the fact that √3 is an irrational number.
∴ Our assumption that (2 -√3) is a rational number is not correct. Thus, (2 - √3) is irrational.
Q8: State whether is a rational number or not.
= 1.23333..... is a non-terminating repeating decimal.
∴is a rational number.
3/4 is in the form of p/q, where q ≠ 0 [Here 4 ≠ 0]
∴ 3/4 is a rational number.
Since the sum of two rational numbers is a rational number.
Therefore,is a rational number.
Q9: The LCM of two numbers is 45 times their HCF. If one of the numbers is 225 and sum of their LCM and HCF is 1150, find the other number.
One of the numbers = 225
Let the other number = x
Also LCM = 45 (HCF) ...(1)
And LCM + HCF =1150
⇒ (45 HCF) + HCF = 1150
⇒ 46 HCF = 1150
⇒ HCF = 1150/46 = 25
From (1),
LCM = 45 × 25
∴ LCM × HCF = (45 × 25) × 25
Now, LCM × HCF = Product of the numbers
∴ x × 225 = (45 × 25) × 25
⇒= 125
Thus, the required number is 125.
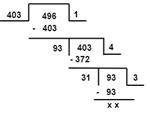
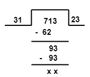
Q10: Three different containers contain 496 litres, 403 litres and 713 litres of a mixture. What is the capacity of the biggest container that can measure all the different quantities exactly?
For the capacity of the biggest container, we have to find the HCF.
HCF: By Long Division method
First find the HCF of two numbers, 496 and 403
The HCF of 496 and 403 = 31
Now find the HCF of 31 and 713
HCF of 713 and 31 is 31
So, the maximum capacity is 31 liters.
Q11: Prove that (5+3√2) is an irrational number.
Sol:
Let (5+3√2) is a rational number.
∴ (5+3√2) = a/b [where ‘a’ and ‘b’ are co-prime integers and b ≠ 0⇒
⇒
⇒‘a’ and ‘b’ are integers,
∴is a rational number.
⇒ √2 is a rational number.
But this contradicts the fact that √2 is an irrational number.
∴ Our assumption that (5+3√2) is a rational is incorrect.
⇒ (5+3√2) is an irrational number.
Q12: Prove that 3-√5 is an irrational number.
Sol:
Let (3-√5) is a rational number.
∴ 3-√5 = p/q , such that p and q are co-prime integers and q ≠ 0.⇒
⇒Since, p and q are integers,
∴is a rational number.
⇒ √5 is a rational number.
But this contradicts the fact that √5 is an irrational number.
∴ Our assumption that (3-√5) is a rational number’ is incorrect.
⇒ (3-√5) is an irrational number.
Q13: Show that there is no positive integer ‘p’ for which 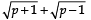 is rational.
is rational.
Sol:
If possible let there be a positive integer p for which
= a/b is equal to a rational i.e. where a and b are positive integers.
Now
Also,
Since a, b are integer
are rationals
⇒ (p + 1) and (p – 1) are perfect squares of positive integers, which is not possible (because any two perfect squares differ at least by 3). Hence, there is no positive integer p for which
is rational.
Q14: Prove that 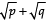 is irrational, where p and q are primes.
is irrational, where p and q are primes.
Sol:
Let
be rational
Let it be equal to ‘r’
i.e.
Squaring both sides, we have
⇒
⇒...(i)
Since, p, q are both rationals
Also, r2 is rational (∵ r is rational)
∴ RHS of (i) is a rational number
⇒ LHS of (i) should be rational i.e.√q should be rational.
But √q is irrational (∵ p is prime).
∴ We have arrived at a contradiction.
Thus, our supposition is wrong.
Hence, √p+√q is irrational.
|
127 videos|655 docs|84 tests
|
FAQs on Class 10 Maths Chapter 1 Question Answers - Real Numbers - 1
| 1. What are real numbers and how are they classified? |  |
| 2. How do you perform operations with real numbers? |  |
| 3. What is the significance of the number line in understanding real numbers? |  |
| 4. Can you explain the difference between rational and irrational numbers? |  |
| 5. How do you solve problems involving real numbers in Class 10 exams? |  |