NCERT Solutions for Class 9 Maths Chapter 4 - Exercise 4.3 Linear Equations in Two Variables
Page: 74
Q.1. Draw the graph of each of the following linear equations in two variables:
(i) x + y = 4
Solution:
To draw a graph of linear equations in two variables, let us find out the points to plot.
To find out the points, we have to find the values which x and y can have, satisfying the equation.
Here,
x + y = 4
Substituting the values for x,
When x = 0,
x+y = 4
0+y = 4
y = 4
When x = 4,
x + y = 4
4 + y = 4
y = 4 – 4
y = 0
x | y |
0 | 4 |
4 | 0 |
The points to be plotted are (0, 4) and (4, 0)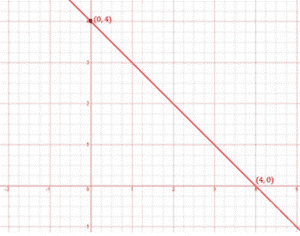
(ii) x – y = 2
Solution:
To draw a graph of linear equations in two variables, let us find out the points to plot.
To find out the points, we have to find the values which x and y can have, satisfying the equation.
Here,
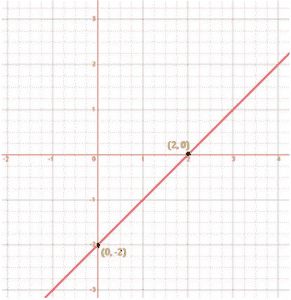
x – y = 2
Substituting the values for x,
When x = 0,
x–y = 2
0 – y = 2
y = – 2
When x = 2,
x–y = 2
2–y = 2
– y = 2–2
–y = 0
y = 0
x | y |
0 | – 2 |
2 | 0 |
The points to be plotted are (0, – 2) and (2, 0)
(iii) y = 3x
Solution:
To draw a graph of linear equations in two variables, let us find out the points to plot.
To find out the points, we have to find the values which x and y can have, satisfying the equation.
Here,
y = 3x
Substituting the values for x,
When x = 0,
y = 3x
y = 3 × 0
y = 0
When x = 1,
y = 3x
y = 3 × 1
y = 3
x | y |
0 | 0 |
1 | 3 |
The points to be plotted are (0, 0) and (1, 3)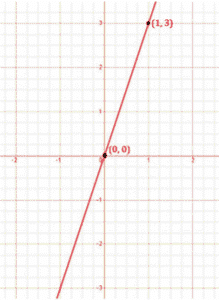
(iv) 3 = 2x + y
Solution:
To draw a graph of linear equations in two variables, let us find out the points to plot.
To find out the points, we have to find the values which x and y can have, satisfying the equation.
Here,
3 = 2x+y
Substituting the values for x,
When x = 0,
3 = 2x + y
3 = 2 × 0 + y
3 = 0 + y
y = 3
When x = 1,
3 = 2x + y
3 = 2 × 1 + y
3 = 2 + y
y = 3 – 2
y = 1
x | y |
0 | 3 |
1 | 1 |
The points to be plotted are (0, 3) and (1, 1)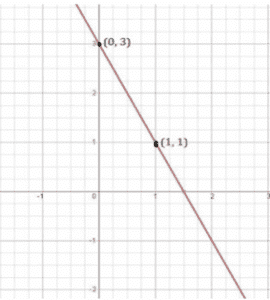
Q.2. Give the equations of two lines passing through (2, 14). How many more such lines are there, and why?
Solution:
We know that infinite number of lines passes through a point.
Equation of 2 lines passing through (2,14) should be in such a way that it satisfies the point.
Let the equation be, 7x = y
7x – y = 0
When x = 2 and y = 14
(7 × 2) -14 = 0
14 – 14 = 0
0 = 0
L.H.S = R.H.S
Let another equation be, 4x = y-6
4x - y + 6 = 0
When x = 2 and y = 14
(4×2–14+6 = 0
8–14+6 = 0
0 = 0
L.H.S = R.H.S
Since both the equations satisfies the point (2,14), than say that the equations of two lines passing through (2, 14) are 7x = y and 4x = y-6
We know that, infinite number of line passes through one specific point. Since there is only one point (2,14) here, there can be infinite lines that passes through the point.
Q.3. If the point (3, 4) lies on the graph of the equation 3y = ax+7, find the value of a.
Solution:
The given equation is
3y = ax + 7
According to the question, x = 3 and y = 4
Now, Substituting the values of x and y in the equation 3y = ax + 7,
We get,
(3 × 4) = (a × 3) + 7
⟹ 12 = 3a + 7
⟹ 3a = 12 – 7
⟹ 3a = 5
⟹ a = 5/3
The value of a, if the point (3,4) lies on the graph of the equation 3y = ax + 7 is 5/3.
Q.4. The taxi fare in a city is as follows: For the first kilometer, the fare is ₹8 and for the subsequent distance it is ₹5 per km. Taking the distance covered as x km and total fare as ₹ y, write a linear equation for this information, and draw its graph.
Solution:
Given,
Total distance covered = x
Total fare = y
Fare for the first kilometer = 8 per km
Fare after the first 1km = 5 per km
If x is the total distance, then the distance after one km = (x - 1)km
i.e., Fare after the first km = 5(x - 1)
According to the question,
The total fare = Fare of first km+ fare after the first km
y = 8 + 5(x - 1)
y = 8 + 5(x - 1)
y = 8 + 5x – 5
y = 5x + 3
Solving the equation,
When x = 0,
y = 5x + 3
y = 5 × 0 + 3
y = 3
When y = 0,
y = 5x + 3
o = 5x + 3
5x = -3
x = -3/5
x | y |
0 | 3 |
-3/5 | 0 |
The points to be plotted are (0, 3) and (-3/5, 0)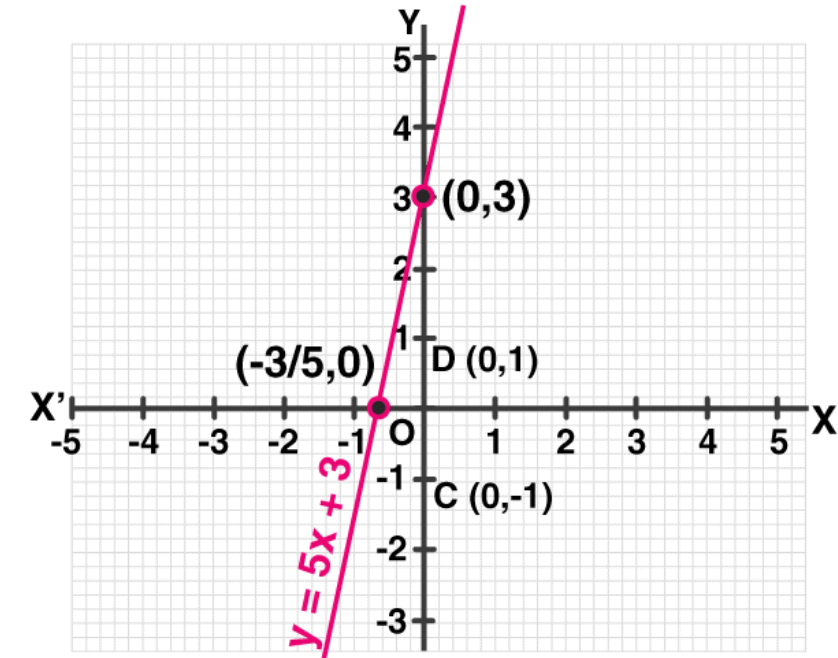
Q.5. From the choices given below, choose the equation whose graphs are given in Fig. 4.6 and Fig. 4.7.
For Fig. 4. 6
(i) y = x
(ii) x + y = 0
(iii) y = 2x
(iv) 2 + 3y = 7x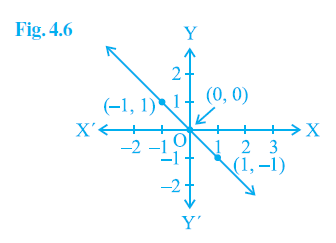
Solution:
The points given in the figure 4.6 are (0,0), (-1,1), (1,-1)
Substituting the values for x and y from these points in the equations, we get,
(i) y = x
(0, 0) ⟹ 0 = 0
(-1, 1) ⟹ -1 ≠ 1 ————————— equation not satisfied
(1, -1) ⟹ 1≠ -1 ————————— equation not satisfied
(ii) x + y = 0
(0,0) ⟹ 0+0 = 0
(-1, 1) ⟹ -1+1 = 0
(1, -1) ⟹ 1+(-1) =0
(iii) y = 2x
(0,0) ⟹ 0 = 2×0
0 = 0
(-1, 1) ⟹ 1 = 2×(-1)
1≠ -2 ————————— equation not satisfied
(1, -1) ⟹ -1 = 2×1
-1 ≠ 2 ————————— equation not satisfied
(iv) 2 + 3y = 7x
(0, 0) ⟹ 2+(30) = 7×0
2 ≠ 0 ————————— equation not satisfied
(-1, 1) ⟹ 2+(3×1) = 7×-1
5 ≠ -7 ————————— equation not satisfied
(1, -1) ⟹ 2+(3×-1) = 7×1
-1 ≠ 7 ————————— equation not satisfied
Since, only equation x + y = 0 satisfies all the points, the equation whose graphs are given in Fig. 4.6 is
x + y = 0
For Fig. 4. 7
(i) y = x + 2
(ii) y = x – 2
(iii) y = –x + 2
(iv) x + 2y = 6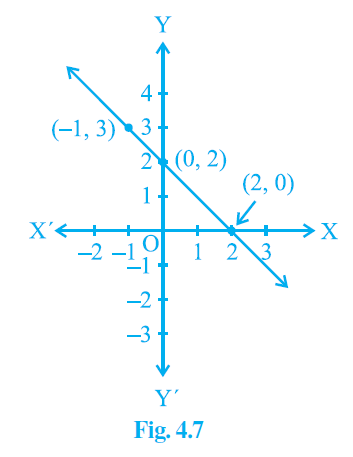
Solution:
The points given in the figure 4.7 are (0,2), (2,0), (-1,3)
Substituting the values for x and y from these points in the equations, we get,
(i) y = x + 2
(0, 2) ⟹2 = 0 + 2
2 = 2
(2, 0) ⟹ 0 = 2 + 2
0 ≠ 4 ————————— equation not satisfied
(-1, 3) ⟹ 3 = -1+2
3 ≠ 1 ————————— equation not satisfied
(ii) y = x – 2
(0, 2) ⟹ 2 = 0 – 2
2 ≠ -2 ————————— equation not satisfied
(2, 0) ⟹ 0 = 2 – 2
0 = 0
(-1, 3) ⟹ 3= –1–2
3 ≠ –3 ————————— equation not satisfied
(iii) y = –x + 2
(0, 2) ⟹ 2 = -0 + 2
2 = 2
(2, 0) ⟹ 0 = -2 + 2
0 = 0
(-1, 3) ⟹ 3= -(-1) + 2
3 = 3
(iv) x + 2y = 6
(0, 2) ⟹ 0 + (2 × 2) = 6
4 ≠ 6 ————————— equation not satisfied
(2, 0) ⟹ 2 + (2 × 0) = 6
2 ≠ 6 ————————— equation not satisfied
(-1, 3) ⟹ -1+ (2 × 3) = 6
5 ≠ 6 ————————— equation not satisfied
Since, only equation y = –x+2satisfies all the points, the equation whose graphs are given in Fig. 4.7 is
y = –x + 2
Q.6. If the work done by a body on application of a constant force is directly proportional to the distance travelled by the body, express this in the form of an equation in two variables and draw the graph of the same by taking the constant force as 5 units. Also read from the graph the work done when the distance travelled by the body is
(i) 2 units
(ii) 0 unit
Solution:
Let the distance traveled by the body be x and the force applied on the body be y.
It is given that,
The work done by a body is directly proportional to the distance travelled by the body.
According to the question,
y ∝ x
y = 5x (5 is a constant of proportionality)
Solving the equation,
(i) when x = 2 units,
then y = 5 × 2 = 10 units
(2, 10)
(ii) when x = 0 units,
then y = 5×0 = 0 units.
(0, 0)
The points to be plotted are (2, 10) and (0, 0)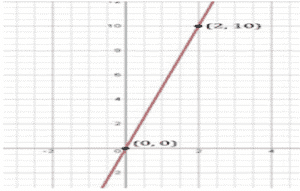
Q.7. Yamini and Fatima, two students of Class IX of a school, together contributed ₹ 100 towards the Prime Minister’s Relief Fund to help the earthquake victims. Write a linear equation which satisfies this data. (You may take their contributions as ₹ x and ₹ y.) Draw the graph of the same.
Solution:
Let Yamini’s donation be ₹x and Fatima’s donation be ₹y
According to the question;
x + y = 100
We know that,
when x = 0 , y = 100
when x = 50, y = 50
when x = 100, y = 0
The points to be plotted are (0, 100), (50, 50), (100, 0)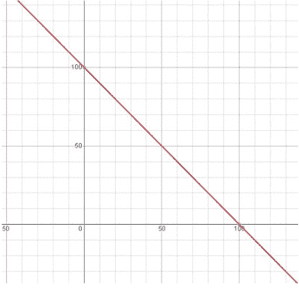
Q.8. In countries like USA and Canada, temperature is measured in Fahrenheit, whereas in countries like India, it is measured in Celsius. Here is a linear equation that converts Fahrenheit to Celsius: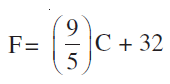
(i) Draw the graph of the linear equation above using Celsius for x-axis and Fahrenheit for y-axis.
(ii) If the temperature is 30°C, what is the temperature in Fahrenheit?
(iii) If the temperature is 95°F, what is the temperature in Celsius?
(iv) If the temperature is 0°C, what is the temperature in Fahrenheit and if the temperature is 0°F, what is the temperature in Celsius?
(v) Is there a temperature which is numerically the same in both Fahrenheit and Celsius? If yes, find it.
Solution:
(i) According to the question,
F = (9/5)C + 32
Solving the equation,
We get,
When C = 0, F = 32
When C = -10 , F = 14
The points to be plotted are (0, 32), (-10, 14)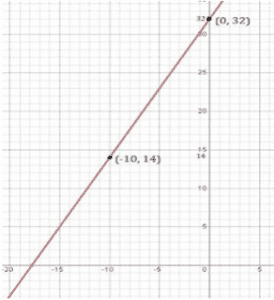 (ii) When C = 30,
(ii) When C = 30,
F = (9/5)C + 32
F = (9 × 30)/5 + 32
= (9 × 6) + 32
= 54 + 32
= 86oF
(iii) When F = 95,
95 = (9/5)C +32
(9/5)C = 95 - 32
(9/5)C = 63
C = (63 × 5)/9
=35oC
(iv) When C = 0,
F = (9/5)C +32
F = (9 × 0)/5 +32
=0 + 32
= 32oF
When F = 0,
0 = (9/5)C + 32
(9/5)C = 0 - 32
(9/5)C = -32
C = (-32 × 5)/9
= -17.7777
= -17.8oC
(v) When F = C,
C = (9/5)C+32
C – (9/5)C = 32
(5-9)C/5 =32
(-4/5)C = 32
(-4/5)C = (-32×5)/4
= – 40oC
Hence, -40o is the temperature which is numerically the same in both Fahrenheit and Celsius.
|
276 docs|155 tests
|
FAQs on NCERT Solutions for Class 9 Maths Chapter 4 - Exercise 4.3 Linear Equations in Two Variables
| 1. What are linear equations in two variables? |  |
| 2. How do you solve a linear equation in two variables? |  |
| 3. Can linear equations in two variables have infinite solutions? |  |
| 4. What is the importance of linear equations in two variables? |  |
| 5. How are linear equations in two variables used in real-life scenarios? |  |

















