NCERT Solutions for Class 9 Maths Chapter 6 - Lines and Angles (Exercise 6.2)
Q1. In the following Figure, if AB CD, CD EF and y : z = 3 : 7, find x.

Ans: It is known that ABCD and CDEF
As the angles on the same side of a transversal line sums up to 180°,
x + y = 180° —–(i)
Also,
O = z (Since they are corresponding angles)
and, y +O = 180° (Since they are a linear pair)
So, y+z = 180°
Now, let y = 3w and hence, z = 7w (As y : z = 3 : 7)
∴ 3w+7w = 180°
Or, 10 w = 180°
So, w = 18°
Now, y = 3×18° = 54°
and, z = 7×18° = 126°
Now, angle x can be calculated from equation (i)
x+y = 180°
Or, x+54° = 180°
∴ x = 126°
Q2. In the following figure, if AB || CD, EF ⊥ CD and ∠GED = 126°, find ∠AGE, ∠GEF and ∠FGE.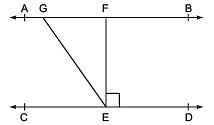 Ans: Since AB || CD, GE is a transversal.
Ans: Since AB || CD, GE is a transversal.
It is given that ∠GED = 126°
So, ∠GED = ∠AGE = 126° (As they are alternate interior angles)
Also,
∠GED = ∠GEF +∠FED
As EF⊥ CD, ∠FED = 90°
∴ ∠GED = ∠GEF+90°
Or, ∠GEF = 126° – 90° = 36°
Again, ∠FGE +∠GED = 180° (Transversal)
Putting the value of ∠GED = 126°, we get
∠FGE = 54°
So,
∠AGE = 126°
∠GEF = 36° and
∠FGE = 54°
Q3. In the following figure, if PQ || ST, ∠PQR = 110° and ∠RST = 130°, find ∠QRS.
[Hint : Draw a line parallel to ST through point R.]

Ans: First, construct a line XY parallel to PQ.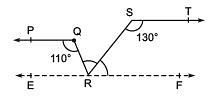
We know that the angles on the same side of transversal is equal to 180°.
So, ∠PQR+∠QRX = 180°
Or, ∠QRX = 180°-110°
∴ ∠QRX = 70°
Similarly,
∠RST +∠SRY = 180°
Or, ∠SRY = 180°- 130°
∴ ∠SRY = 50°
Now, for the linear pairs on the line XY-
∠QRX+∠QRS+∠SRY = 180°
Putting their respective values, we get
∠QRS = 180° – 70° – 50°
Hence, ∠QRS = 60°
Q4. In the following figure, if AB || CD, ∠ APQ = 50° and ∠ PRD = 127°, find x and y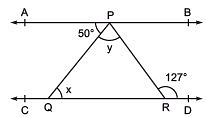 Ans: From the diagram,
Ans: From the diagram,
∠APQ = ∠PQR (Alternate interior angles)
Now, putting the value of ∠APQ = 50° and ∠PQR = x, we get
x = 50°
Also,
∠APR = ∠PRD (Alternate interior angles)
Or, ∠APR = 127° (As it is given that ∠PRD = 127°)
We know that
∠APR = ∠APQ+∠QPR
Now, putting values of ∠QPR = y and ∠APR = 127°, we get
127° = 50°+ y
Or, y = 77°
Thus, the values of x and y are calculated as:
x = 50° and y = 77°
Q5. In the following figure, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB || CD.
Ans: First, draw two lines, BE and CF, such that BE ⊥ PQ and CF ⊥ RS.
Now, since PQ || RS,
So, BE || CF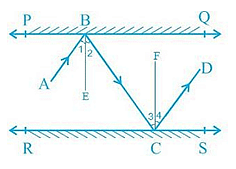
We know that,
Angle of incidence = Angle of reflection (By the law of reflection)
So,
∠1 = ∠2 and
∠3 = ∠4
We also know that alternate interior angles are equal. Here, BE ⊥ CF and the transversal line BC cuts them at B and C
So, ∠2 = ∠3 (As they are alternate interior angles)
Now, ∠1 +∠2 = ∠3 +∠4
Or, ∠ABC = ∠DCB
So, AB || CD (alternate interior angles are equal)
|
5 videos|378 docs|164 tests
|
FAQs on NCERT Solutions for Class 9 Maths Chapter 6 - Lines and Angles (Exercise 6.2)
| 1. What are the different types of angles? |  |
| 2. How can I identify parallel lines? |  |
| 3. What is the sum of the angles in a triangle? |  |
| 4. How can I find the measure of an angle using a protractor? |  |
| 5. Can two lines intersect at more than one point? |  |

|
Explore Courses for CAT exam
|

|


















