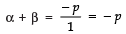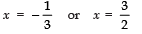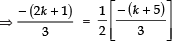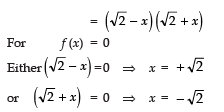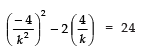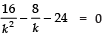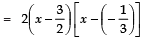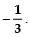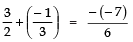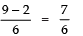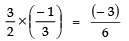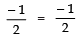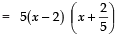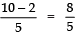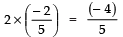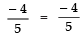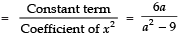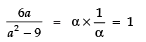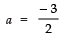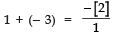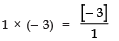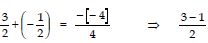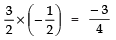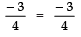Class 10 Maths Chapter 2 Question Answers - Polynomials - 1
Q1: Find the sum and product of zeroes of 3x2 - 5x + 6.
Here, p (x) = 3x2 - 5x + 6
Comparing it with ax2 + bx + c, we have
a = 3, b = - 5, c = 6Sum of the zeroes:
= - Coefficient of x / Coefficient of x2 = - (-5)/3 = 53
Product of the zeroes:
= Constant term / Coefficient of x2 = 6/3 = 2
Q2: Find the sum and product of the zeroes of polynomial p (x) = 2x3 - 5x2 - 14x + 8.
Comparing p (x) = 2x3 - 5x2 - 14x + 8 with ax3 + bx2 + cx + d, we have
a = 2, b = –5,
c = - 14 and d = 8Sum of the zeroes:
= -b/a = -(-5)/2 = 5/2Product of the zeroes:
= -d/a = -8/2 = -4
Q3: Find a quadratic polynomial whose zeroes are: 2 + √5 / 2 and 2 - √5 / 2 .
Sum of zeroes (S):
(2 + √5)/2 + (2 - √5)/2 = 4/2 = 2
Product of zeroes (P):(2 + √5)/2 × (2 - √5)/2 = [2² - (√5)²]/4 = 4 - 5/4 = -1/4
Quadratic Polynomial:
The required quadratic polynomial is:
k(x² - Sx + P), where k is any real number.
Substituting the values of S and P:
k(x² - 2x + (-1/4)) = k(x² - 2x - 1/4)Thus, the required polynomial is
= k (x2 - 2x - 1/4)
Q4: If α and β are the zeroes of a Quadratic polynomial x2 + x - 2 then find the value of .
Comparing x2 + x - 2 with ax2 + bx + c, we have:
a = 1, b = 1, c = - 2Sum of roots (α + β) = -ba = -(1)/1 = -1
Product of roots (αβ) = ca = (-2)/1 = -2
To find:
1/α - 1/β
Solution:
1/α + 1/β = β - α/αβ = -(-3)/-2 = 3/2
Now, calculate (α - β):
(α - β)² = (α + β)² - 4αβ
(α - β)² = 1² - 4(-2)
(α - β)² = 1 + 8 = 9
(α - β) = ±√9 = ±3Therefore:
1/α - 1/β = - 3/2
Q5: If a and b are the zeroes of x2 + px + q then find the value of ( αβ + 2) ( βα + 2).
Comparing x2 + px + q with ax2 + bx + c
a =1, b = p and c = q
∴ Sum of zeroes, a + b = - b/a
⇒
and αβ = c/a
⇒ αβ = q/1 = q
Now,= αβ + 2αβ + 2βα + 4
Substituting α + β = -p and αβ = q:
= 5 + 2[ (α + β)² - 2αβαβ]Further simplifying:
= 5 + 2[ p² - 2qq]Final Result:
The value of the given expression is:
( αβ + 2) ( βα + 2) = 2p² + qq
Q6: Find the zeroes of the quadratic polynomial 6x2 - 3 - 7x.
We have,
= 6x2 - 3 - 7x = 6x2 - 7x - 3
= 6x2 - 9x + 2x - 3
= 3x (2x - 3) + 1 (2x - 3)
= (3x + 1) (2x - 3)
For 6x2 - 3 - 7x to be equal to zero,
either (3x + 1) = 0 or (2x - 3) = 0
⇒ 3x = - 1 or 2x = 3
⇒
Thus, the zeroes ofand 3/2.
Q7: Find the zeroes of 2x2 - 8x + 6.
We have,
2x2 - 8x + 6 = 2x2 - 6x - 2x + 6
= 2x (x - 3) - 2 (x - 3)
= (2x - 2) (x - 3)
= 2 (x - 1) (x - 3)
For 2x2 - 8x + 6 to be zero,
Either, x - 1 = 0 ⇒ x = 1
or x - 3 = 0 ⇒ x = 3
∴ The zeroes of 2x2 - 8x + 6 are 1 and 3.
Q8: Find the zeroes of the quadratic polynomial 3x2 + 5x - 2.
We have,
p (x) = 3x2 + 5x - 2
= 3x2 + 6x - x - 2
= 3x (x + 2) - 1 (x + 2)
= (x + 2) (3x - 1)
For p (x) = 0, we get
Either x + 2 = 0 ⇒ x = - 2
or 3x - 1 = 0 ⇒ x = 1/3
Thus, the zeroes of 3x2 + 5x - 2 are - 2 and 1/3.
Q9: If the zero of a polynomial p (x) = 3x2 - px + 2 and g (x) = 4x2 - q x - 10 is 2, then find the value of p and q.
∵ p (x) = 3x2 - px + 2
∴ p (2) = 3 (2)2 - p (2) + 2 = 0
[2 is a zero of p (x)]
or 12 - 2p + 2 or 14 - 2p = 0
or p = 7
Next g (x) = 4x2 - q x - 10
∴ g (2) = 4(2)2 - Q (2) - 10 = 0
[2 is a zero of g (x)]
or 4 × 4 - 2q - 10 = 0
or 16 - 2q - 10 = 0
or 6 - 2q = 0
⇒ q = 6/2 ⇒ q = 3
Thus, the required values are p = 7 and q = 3.
Q10: Find the value of ‘k’ such that the quadratic polynomial 3x2 + 2kx + x - k - 5 has the sum of zeroes as half of their product.
Here, p (x) = 3x2 + 2kx + x - k - 5
= 3x2 + (2k + 1) x - (k + 5)
Comparing p (x) with ax2 + bx + c, we have:
a = 3, b = (2k + 1),
c = - (k + 5)
∴ Sum of the zeroes
Product of the zeroes
According to the condition,
Sum of zeroes = 1/2 (product of roots)
⇒ - 2 (2k + 1) = - (k + 5)
⇒ 2 (2k + 1) = k + 5
⇒ 4k + 2 = k + 5
⇒ 4k - k = 5 - 2
⇒ 3k = 3
⇒ k = 3/3 = 1
Q11: Find the zeroes of the polynomial f (x) = 2 - x2.
We have f (x)= 2 - x2
= (√2 )2 - x2
Q12: Find the cubic polynomial whose zeroes are 5, 3 and - 2.
∵ 5, 3 and - 2 are zeroes of p (x)
∴ (x - 5), (x - 3) and (x + 2) are the factors of p (x)
⇒ p (x) = k (x - 5) (x - 3) (x + 2)
= k (x2 - 8x + 15) (x + 2)
= k (x3 - 8x2 + 15x + 2x2 - 16x + 30
= k (x3 + [- 8 + 2] x2 + [15 - 16] x + 30)
= k (x3 - 6x2 - x + 30)
Thus, the required polynomial is k (x3 - 6x2 - x + 30).
Q13: If α, β and γ be the zeroes of a polynomial p (x) such that (α + β +γ) = 3, (αβ + βγ + γα) = -10 and αβγ = - 24 then find p (x).
Here, α + β + γ = 3
αb + βγ + γα = - 10
αβγ = - 24
∵ A cubic polynomial having zeroes as α,β,γ is
p (x) = x3 - (a + b + γ) x2 + (αβ + βγ + γα) x - (αβγ)
∴The required cubic polynomial is
= k {x3 - (3) x2 + (- 10) x - (- 24)}
= k(x3 - 3x2 - 10x + 24)Note: If α, β and γ be the zeroes of a cubic polynomial p (x) then
p (x) = x3 - [Sum of the zeroes] x2 + [Product of the zeroes taken two at a time] x - [Product of zeroes]
i.e., p (x) = k {x3 - (α + β + γ) x2 + [αβ + βγ + γα] x - (αβγ).
Q14: If α and β are the zeroes of the quadratic polynomial p (x) = kx2 + 4x + 4 such that α2 + β2 = 24, find the value of k.
Here, p (x) = kx2 + 4x + 4.
Comparing it with ax2 + bx + c, we have:
a = k; b = 4; c = 4
∴ Sum of the zeroes = -b/a
⇒ α + β = -4/k
and Product of the zeroes = c/a
⇒ αβ = 4/k
∵ α2 + β2 = 24
∴ (α + β)2 - 2αβ = 24
[∵ (x + y)2 = x2 + y2 + 2xy ⇒ (x + y)2 - 2xy = x2 + y2]
⇒
⇒
⇒ 16 − 8k − 24k2 =0
⇒ 24k2 + 8k − 16 = 0
⇒ (3k − 2) (k + 1) = 0
⇒ 3k − 2= 0 or k + 1 = 0
⇒ k = 2/3 or k = -1
Q15: Find the zeroes of the quadratic polynomial 6x2 - 3 - 7x and verify the relationship between the zeroes and the coefficients of the polynomial.
Here, p (x) = 6x2 - 3 - 7x = 6x2 - 7x - 3
= 6x2 - 9x + 2x - 3
= 3x (2x - 3) + 1 (2x - 3)
= (2x - 3) (3x + 1)
=
∴ Zeroes of p (x) are 3/2 and
To verify the relationship:
Sum of the zeroes = - coefficient of x/coefficient of x²⇒
⇒
⇒ 7/6 = 7/6
L.H.S = R.H.S ⇒ Relationship is verified.
Product of the zeroes = Constant term/coefficient of x²⇒
⇒
i.e., L.H.S = R.H.S ⇒ Relationship is verified.
Q16: Find the zeroes of the quadratic polynomial 5x2 - 4 - 8x and verify the relationship between the zeroes and the coefficients of the polynomial.
p (x) = 5x2 - 4 - 8x
= 5x2 - 8x - 4
= 5x2 - 10x + 2x - 4
= 5x (x - 2) + 2 (x - 2)
= (x - 2) (5x + 2)
∴ zeroes of p (x) are 2 and
Relationship Verification
Sum of the zeroes = - coefficient of x/coefficient of x²
⇒
⇒
⇒ 8/5 = 8/5i.e., L.H.S. = R.H.S. ⇒ relationship is verified.
Product of the zeroes = Constant term/coefficient of x²
⇒
⇒
i.e., L.H.S. = R.H.S.
⇒ The relationship is verified.
Q17: Find the quadratic polynomial, the sum of whose zeroes is 8 and their product is 12. Hence, find the zeroes of the polynomial.
The quadratic polynomial p (x) is given by
x2 - (Sum of the zeroes) x + (Product of the zeroes)
∴ The required polynomial is
= x2 - [8] x + [12]
= x2 - 8x + 12
To find zeroes:
∵ x2 - 8x + 12 = x2 - 6x - 2x + 12
= x (x - 6) - 2 (x - 6)
= (x - 6) (x - 2)
∴ The zeroes of p (x) are 6 and 2.
Q18: If one zero of the polynomial (a2 - 9) x2 + 13x + 6a is reciprocal of the other, find the value of ‘a’.
Here, p (x) = (a2 - 9) x2 + 13x + 6a
Comparing it with Ax2 + Bx + C, we have:
A = (a2 - 9); B = 13; C = 6
Let one of the zeroes = a
∴ The other zero = 1/α
Now, Product of the zeroes⇒
⇒ 6a = a2 − 9 ⇒ a2 − 6a + 9 = 0
⇒ (a − 3)2 =0 ⇒ a − 3=0
⇒ a = 3
Thus, the required value of a is 3.
Q19: If the product of zeroes of the polynomial ax2 - 6x - 6 is 4, find the value of ‘a’
Here, p (x) = ax2 - 6x - 6
∵ Product of zeroes = Constant term/coefficient of x²
but product of zeroes is given as 4
∴⇒ − 6 = 4 × a
⇒⇒
Thus, the required value of a is -3/2.
Q20: Find the quadratic polynomial whose zeroes are 1 and - 3. Verify the relation between the coefficients and the zeroes of the polynomial.
The given zeroes are 1 and - 3.
∴ Sum of the zeroes = 1 + (- 3) = - 2
Product of the zeroes = 1 × (- 3) = - 3
A quadratic polynomial p (x) is given by
x2 - (sum of the zeroes) x + (product of the zeroes)
∴ The required polynomial is
x2 - (- 2) x + (- 3)
⇒ x2 + 2x - 3
Verification of relationship
∵ Sum of the zeroes Constant term/coefficient of x²∴
⇒− 2= − 2i.e., L.H.S = R.H.S ⇒ The sum of zeroes is verified
∵ Product of the zeroes = Constant term/coefficient of x²
∴
⇒− 3= − 3i.e., L.H.S = R.H.S ⇒ The product of zeroes is verified.
Q21: Find the zeroes of the quadratic polynomial 4x2 - 4x - 3 and verify the relation between the zeroes and its coefficients.
Here, p (x) = 4x2 - 4x - 3 = 4x2 - 6x + 2x - 3
= 2x (2x - 3) + 1 (2x - 3)
= (2x - 3) (2x + 1)
=
∴are zeroes of p (x).
Verification of relationship
∵ Sum of the zeroes = - coefficient of x/coefficient of x²∴
⇒ 3 - 1 2
⇒ 2/2 = 1 ⇒ 1= 1
⇒
2/2 = 1 ⇒ 1 = 1
i.e., L.H.S = R.H.S ⇒ Sum of zeroes is verified
Now, Product of zeroes =Constant term/coefficient of x²
⇒
i.e., L.H.S = R.H.S ⇒ Product of zeroes is verified.
Q22: Find a quadratic polynomial whose zeroes are - 4 and 3 and verify the relationship between the zeroes and the coefficients.
We know that:
P (x) = x2 - [Sum of the zeroes] x + [Product of the zeroes] ...(1)
∵ The given zeroes are - 4 and 3
∴ Sum of the zeroes = (- 4) + 3 = - 1
Product of the zeroes = (- 4) × 3 = - 12
From (1), we have
x2 - (- 1) x + (- 12)
= x2 + x - 12 ...(2)
Comparing (2) with ax2 + bx + c, we have
a = 1, b = 1, c = - 12
∴ Sum of the zeroes = -b/a
⇒ (+ 3) + (- 4) = -1/1
i.e., L.H.S = R.H.S ⇒ Sum of zeroes is verified.
Product of zeroes = c/a
⇒ 3 × (- 4) = -12/1
⇒ - 12 = - 12
i.e., L.H.S = R.H.S ⇒ Product of roots is verified.
Q23: Find the zeroes of the polynomial x² + (1/6)x - 2 and verify the relation between the coefficients and the zeroes of the above polynomial.
The given polynomial is x² + (1/6)x - 2
Step 1: Write as:
= 6x² + x - 12/6Step 2: Expand:
= 6x² + 9x - 8x - 12/6Step 3: Factorize:
= 3x(2x + 3) - 4(2x + 3)/6Step 4: Take common factors:
= (3x - 4)(2x + 3)/6∴ zeroes of the given polynomial are 4/3 and - 3/2
Now in, x² + 16x - 2
co-efficient of x2 = 1
co-efficient of x = 1/6
constant term = –2
Sum of zeroes = 4/3 + -3/2 = 1/6 = coefficient of x/coefficient of x²Product of zeroes = 4/3 × -3/2 = -2 = constant term/coefficient of x²
Q24: Find the quadratic polynomial, the sum and product of whose zeroes are √2 and -3/2 respectively. Also, find its zeroes.
Sum of zeroes = √2
Product of zeroes = -3/2
∴ A quadratic polynomial is given by:
x² - [sum of roots]x + [product of roots]
∴ The required polynomial is:
x² - √2x + -(3/2)Since:
x² - √2x - (3/2) = (2x² - 2√2x - 3)/2
= 1 [2x² + √2x - 3(2x - 3)]/2
= 1 [(√2x)(√2x + 1) - 3(√2x - 3)]/2
= 1 [(√2x + 1)(√2x - 3)]/2⇒ Zeroes are -1/√2 and 3/√2
Q25: If a and b are zeroes of the quadratic polynomial x2 – 6x + a; find the value of ‘a’ if 3α + 2β = 20.
We have quadratic polynomial = x2 – 6x + a ...(1)
∵ a and b are zeroes of (1)
∴
It is given that: 3α + 2β = 20 ...(2)
Now, α +β = 6 ⇒ 2 (α+ β) = 2(6)
2α + 2β = 12 ...(3)
Subtracting (3) from (2), we have
Substituting a = 8 in α + β= 6, we get
8 +β = 6 ⇒ β = –2
Since, αβ = a
8(–2) = α ⇒ α = –16
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Maths Chapter 2 Question Answers - Polynomials - 1
| 1. What are polynomials and how are they classified? |  |
| 2. How do you add and subtract polynomials? |  |
| 3. What is the process for multiplying polynomials? |  |
| 4. How do you factor polynomials? |  |
| 5. What is the Remainder Theorem and how is it applied? |  |