Facts that Matter: Pair of Linear Equations in Two Variables | Mathematics (Maths) Class 10 PDF Download
Linear Equation in Two Variable
An equation that can be put in the form
ax + by + c = 0
where a, b and c are real numbers (a, b ≠ 0) is called a linear equation in two variables ‘x’ and ‘y’.
General Form of a Pair of Linear Equations in Two Variable
The general form of a linear pair of equations in two variables is:
a1x + b1y + c1 = 0 and
a2x + b2y + c2 = 0
where a1, b1, c1, a2, b2, c2 are real numbers such that the coefficients of x and y cannot be zero simultaneously.
Solution of a Pair of Linear Equations in Two Variables
The solution of a linear equation in two variables ‘x’ and ‘y’ is a pair of values (one for ‘x’ and other for ‘y’) which makes the two sides of the equation equal.
There are two methods to solve a pair of linear equations:
Algebraic Method
There are 3 algebraic methods for solving a pair of linear equations in two variables.
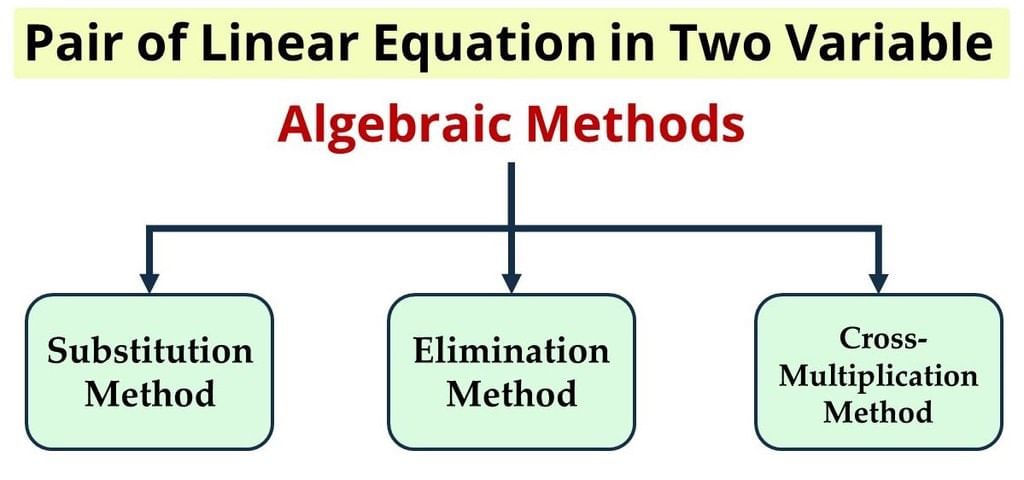 Types of Algebraic Methods
Types of Algebraic Methods
(i) Substitution Method
Step 1: Find the value of one variable, say y in terms of the other variable, i.e., x from either equation, whichever is convenient
Step 2: Substitute this value of y in the other equation, and reduce it to an equation in one variable, i.e., in terms of x, which can be solved. Sometimes, you will get statements with no variables. If this statement is true, you can conclude that the pair of equations has infinitely many solutions. If the statement is false, then the pair of linear equations is inconsistent.
Step 3: Substitute the value of x (or y) obtained in Step 2 in the equation used in Step 1 to obtain the value of the other variable.
(ii) Elimination Method
Step 1: First, multiply both the equations by some suitable non-zero constants to make the coefficients of one variable (either x or y) numerically equal.
Step 2: Then add or subtract one equation from the other so that one variable gets eliminated. After you get an equation in one variable, go to step 3.
If in Step 2, you obtain a true statement involving no variable, then the original pair of equations has infinitely many solutions.
If in Step 2, you obtain a false statement involving no variable, then the original pair of equations has no solution, i.e., it is inconsistent.
Step 3: Solve the equation in one variable(x or y) so obtained to get its value.
Step 4: Substitute this value of x ( or y) in either of the original equations to get the value of the other variable.
Graphical Method
(i) If the graphs of two equations of a system intersect at a point, the system is said to have a unique solution, i.e., the system is consistent.
(ii) If the graphs of two equations of a system are two parallel lines, the system is said to have no solution, i.e., the system is inconsistent.
(iii) When the graphs of two equations of a system are two coincident lines, the system is said to have infinitely many solutions, i.e., the system is consistent and dependent.
Consistent and Inconsistent System
If 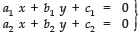
form a pair of linear equations, then the following three situations can arise:
(i) If, then the system is consistent.
(ii) If , then the system is inconsistent.
(iii) If , then the system is dependent and consistent.
|
127 videos|584 docs|79 tests
|
FAQs on Facts that Matter: Pair of Linear Equations in Two Variables - Mathematics (Maths) Class 10
| 1. What is a pair of linear equations in two variables? |  |
| 2. How can we solve a pair of linear equations in two variables? |  |
| 3. What is the substitution method for solving a pair of linear equations in two variables? |  |
| 4. How does the elimination method work for solving a pair of linear equations in two variables? |  |
| 5. What is the graphical method for solving a pair of linear equations in two variables? |  |






















