NCERT Solutions for Class 9 Maths Chapter 9 - Exercise 9.2 Areas of Parallelograms and Triangles
Q1. In the figure, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.
Ans: We have AE ⊥ DC and AB = 16 cm
∵ AB = CD [opp. sides of parallelogram ABCD]
∴ CD = 16 cm
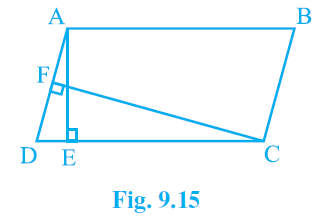
Now, area of parallelogram ABCD= CD x AE = 16 x 8 cm2 [∴ AE = 8 cm (Given)]
= 128 cm2
Since, CF ⊥ AD
∴ Area of parallelogram ABCD = AD x CF
⇒ AD x CF = 128
⇒ AD x 10 = 128 [∵ CF = 10 cm]
⇒ AD = (128/10)
= 12.8
Thus, the required length of AD is 12.8 cm.
Q2. If E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that: ar (EFGH) = (1/2) ar (ABCD).
Ans: Let us join E and G.
Remember
If a triangle and a parallelogram are on the same base and between the same parallels, then the area of the triangle is equal to half the area of the parallelogram.
∵ E and G are the mid-points of AB and CD respectively.
∴ EG is parallel to BC or AD.
Also, ar (parallelogram EBCG) = ar (parallelogram AEGD)
= (1/2) ar (parallelogram ABCD) …(1)
Now, ΔEFG and parallelogram EBCG are on the same base EG, and between the same parallels EG and BC.
∴ ar (ΔEFG) = (1/2) ar (parallelogram EBCG) …(2)
Similarly, ar (ΔEHG) = (1/2)
ar (parallelogram AEGD) …(3)
Adding (2) and (3), we get
ar (ΔEFG) + ar (ΔEHG)
= (1/2) [ar (parallelogram EBCG) + ar (parallelogram AEGD)]
⇒ ar (EFGH)
=(1/2) [ (1/2)ar (parallelogram ABCD) + (1/2)ar (parallelogram ABCD)]
[from (1)]
⇒ ar (EFGH) =(1/2)[ar (parallelogram ABCD)]
Thus, ar (EFGH) = (1/2)ar (ABCD).
Note: By joining H and F, we can also have
ar (ΔHEF) + ar (ΔHGF)
= (1/2) [(1/2)ar (parallelogram ABCD) + (1/2)ar (parallelogram ABCD)]
⇒ ar (EFGH) =(1/2) ar (ABCD)
Q3. ‘P’ and ‘Q’ are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (ΔAPB) = ar(ΔBQC).
Ans: ∵ ABCD is a parallelogram.
∴ AB || CD and BC || AD.
Now, ΔAPB and parallelogram ABCD are on the same base AB and between the same parallels AB and CD.
∴ ar (ΔAPB) =(1/2) ar (parallelogram ABCD) …(1)
Also, ΔBQC and parallelogram ABCD are on the same base BC and between the same parallels BC and AD.
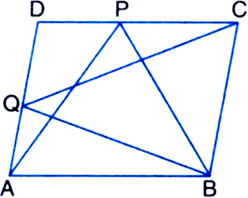
∴ ar (ΔBQC) = (1/2) ar (parallelogram ABCD) …(2)
From (1) and (2), we have ar (ΔAPB) = ar (ΔBQC).
Q4. In the figure, P is a point in the interior of a parallelogram ABCD. Show that
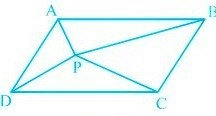
(i) ar (ΔAPB) + ar (ΔPCD) = (1/2) ar (ABCD)
(ii) ar (ΔAPD) + ar (ΔPBC) = ar (ΔAPB) + ar (ΔPCD) Hint: Through P, draw a line parallel to AB.
Ans:
(i) We have a parallelogram ABCD, i.e. AB || CD and BC || AD.
Let us draw EF || AB, through P.
Since AB || EF,
∴ ΔAPB and parallelogram AEFB are on the same base AB and between the same parallels AB and EF.
∴ ar (ΔAPB) = (1/2)ar (AEFB) …(1)
Also, Δ(PCD) and parallelogram CDEF are on the same base CD and between the same parallels CD || EF.
ar (ΔPCD) = (1/2)ar (parallelogram CDEF) …(2)
Adding (1) and (2), we have ar (ΔAPB) + ar (ΔPCD)
= (1/2)ar (AEFB) + (1/2)ar (CDEF)
⇒ ar (ΔAPB) + ar (ΔPCD) = (1/2)ar (ABCD)
(ii) Let us join GH || BC, through P.
∴ ΔAPD and parallelogram ADGH are on the same base AD and between the same parallels AD and GH.
∴ ar (ΔAPD) = (1/2) ar (ADGH) …(3)
Similarly, ar (ΔPBC) =(1/2) ar (BCGH) …(4)
Adding (3) and (4), we have ar (ΔAPD) + ar (ΔPBC)
=(1/2) ar (ADGH) +(1/2) ar (BCGH)
ar (ΔAPD) + ar (ΔPBC) =(1/2) ar (ABCD) …(5)
But, ar (ΔAPB) + ar (ΔPCD) =(1/2) ar (ABCD) …(6)
From (5) and (6), we have: ar (ΔAPD) + ar (ΔPBC) = ar (ΔAPB) + ar (ΔPCD)
Q5. In the figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
(i) ar (PQRS) = ar (ABRS) (ii) ar (AXS) = (1/2) ar (PQRS)
Ans: We have two parallelograms ABRS and PQRS and a point X on BR.
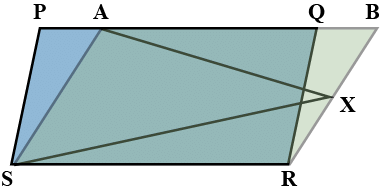
(i) To prove that ar (PQRS) = ar (ABRS)
∵ Parallelogram PQRS and parallelogram ABRS are on the same base RS and between the same parallels RS and PAQB.
∴ ar (PQRS) = ar (ABRS)
(ii) To prove that ar (AXS) = (1/2) ar (PQRS)
∵ ΔAXS and parallelogram ABRS are on the same base AS and between the same parallels AS and BR.
∴ ar (ΔAXS) = (1/2) ar (ABRS) …(1)
But ar (parallelogram PQRS) = ar (parallelogram ABRS) (Proved) …(2)
From (1) and (2), we have ar (ΔAXS)
= (1/2) ar (parallelogram PQRS)
Q6. A farmer was having a field in the form of a parallelogram PQRS. She took any point ‘A’ on RS and joined it to ‘P’ and ‘Q’. In how many parts the field is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately.
How should she do it?
Ans: The farmer is having the field in the form of parallelogram PQRS, and point A is situated at RS.
Let us join AP and AQ.
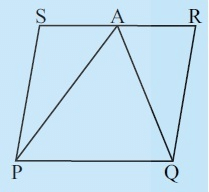
Obviously, the field is divided into three parts i.e. in ΔAPS, ΔPAQ and ΔQAR, i.e these parts are triangular in shape.
Since ΔPAQ and parallelogram PQRS are on the same base and between the same parallels PQ and RS.
∴ ar (ΔPAQ) =(1/2) ar (parallelogram PQRS) …(1)
⇒ ar (parallelogram PQRS) - ar (ΔPAQ) = ar (parallelogram PQRS) - (1/2) ar (parallelogram PQRS)
⇒ [ar (ΔAPS) + ar (ΔQAR)] = (1/2) ar (parallelogram PQRS) …(2)
From (1) and (2), we have ar (ΔPAQ) = ar [(ΔAPS) + (ΔQAR)]
Thus, the farmer can sow wheat in (ΔPAQ) and pulses in [(ΔAPS) + (ΔQAR)] OR
wheat in [(ΔAPS) + (ΔQAR)] and pulses in (ΔPAQ).
|
276 docs|155 tests
|
FAQs on NCERT Solutions for Class 9 Maths Chapter 9 - Exercise 9.2 Areas of Parallelograms and Triangles
| 1. What is the formula to find the area of a parallelogram? |  |
| 2. How is the area of a triangle related to the area of a parallelogram? |  |
| 3. Can the area of a parallelogram be negative? |  |
| 4. What are the different ways to find the height of a parallelogram? |  |
| 5. Can the area of a parallelogram be equal to the sum of the areas of two triangles? |  |

















