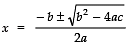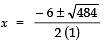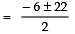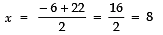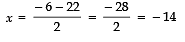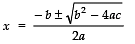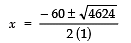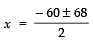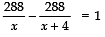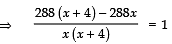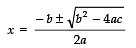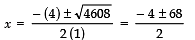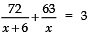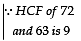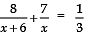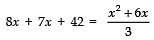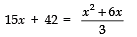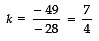Class 10 Maths Chapter 4 Question Answers - Quadratic Equations
Q1: A two-digit number is 5 times the sum of its digits and is also equal to 5 more than twice the product of its digits. Find the number.
Let the tens digit = x
And the ones digit = y
∴ The number = 10x + y
According to the conditions,
10x + y = 5 (x + y) ...(1)
10x + y = 2xy + 5 ...(2)
From (1), we have
10x + y = 5x + 5y
⇒ 10x + y − 5x − 5y =0
⇒ 5x − 4y = 0⇒
⇒ 40x + 5x = 10x2 + 20 [Multiplying both sides by 4]
⇒ 45x = 10x2 + 20
⇒ 10x2 − 45x − 20 = 0
⇒ 2x2 − 9x − 4= 0
⇒ 2x2 − 8x − x + 4 = 0
⇒2x (x − 4) − 1 (x − 4) = 0
⇒ (x − 4) (2x − 1) = 0
Either x − 4 = 0 ⇒ x = 4
or 2x − 1 = 0 ⇒ x = 1/2
But a digit cannot be a fraction,
∴ x = 4
⇒ The tens digit = 4
∴ x = 4 and y = 5
∴ The required number = 10 × 4 + 5
= 40 + 5 = 45
Q2: The denominator is one more than twice the numerator. If the sum of the fraction and its reciprocal is  find the fraction.
find the fraction.
Let the numerator be x
∴ Denominator = (2x + 1)
∴ Fraction = x/(2x +1)
Reciprocal of the fraction = 2x +1/x
According to the condition,
⇒
⇒
⇒
⇒ 21 (5x2 + 4x + 1) = 58 (2x2 + x)
⇒ 105x2 + 84x + 21 = 116x2+ 58x
⇒ 105x2 − 116x2 + 84x − 58x + 21 = 0
⇒ − 11x2 + 26x + 21 = 0
⇒ 11x2 − 26x − 21 = 0 ...(1)Comparing (1) with ax2 + bx + c = 0, we have:
a =11
b = − 26
c = − 21
∴ b2 − 4ac =(− 26)2 − 4 × 11 (− 21) = 676 + 924 = 1600
Since,
∴
⇒Taking the +ve sign,
Taking the −ve sign,
But the numerator cannot be -7/11
∴ x = 3 ⇒ The numerator = 3
∴ Denominator = 2 (3) + 1 = 7
Thus, the required fraction = 3/7
Q3: The sum of a number and its reciprocal is 10/3. Find the number.
Let the required number = x
∴ Its reciprocal = 1/x
According to the condition, we have:
⇒
⇒⇒ 3 (x2 + 1) = 10x
⇒ 3x2 + 3 − 10x = 0
⇒ 3x2 − 10x + 3 = 0
⇒ 3x2 − 9x − x + 3 = 0
⇒ 3x (x − 3) − 1 (x − 3) = 0
⇒ (x − 3) (3x − 1) = 0Either x −3 = 0 ⇒ x = 3
or 3x − 1 = 0 ⇒ x = 1/3
Thus, the required number is 3 or 1/3.
Q4: The hypotenuse of a right triangle is  cm. If the smaller side is tripled and the longer side doubled, the new hypotenuse will be
cm. If the smaller side is tripled and the longer side doubled, the new hypotenuse will be  cm. How long are the sides of the triangle?
cm. How long are the sides of the triangle?
Let the smaller side = x
∴ Longer side =
According to the condition, we have [3 (Smaller side)]2 + [2 (Longer side)]2 = [New Hypotenuse]
⇒ 5x2 = 405 − 360
⇒ 5x2 = 45
⇒
⇒
But x = − 3 is not required, because the side of a triangle cannot be negative.
∴ x = 3 ⇒ Smaller side = 3 cm
∴ Longer side
Thus, the required sides of the triangle are 3 cm and 9 cm.
Q5: A motorboat goes 10 km upstream and returns back to the starting point in 55 minutes. If the speed of the motorboat in still water is 22 km/hr, find the speed of the current.
Let the speed of the current = x km/hr
∴ The speed downstream = (22 + x) km/hr
The speed upstream= (22 − x) km/hrSince, Time = Distance/Speed
∴ Time for going 10 km downstream
Time for returning back 10 km upstream
According to the condition,
⇒[∵ 55 minutes = 55/60 hours]
⇒
⇒ 11 (484 − x2) = 120 × 44
⇒ 5324 − 11x2 = 5280
⇒ 11x2 = 5324 − 5280 = 44
⇒
⇒ x = ± 2
But speed of the current cannot be negative,∴ x = 2
⇒ Speed of current = 2 km/hr
Q6: A motorboat whose speed in still water is 5 km/hr, takes 1 hour more to go 12 km upstream than to return downstream to the same spot. Find the speed of the stream.
Let the speed of the stream be x km/hr ∴ Downstream speed of the motor boat = (x + 5) km/hr
⇒ Time taken to go 12 km upstream= 12/5 − x hours
Time taken to return 12 km downstream
= 12/5 + x hours
According to the condition
∴12 (5 + x) − 12 (5 − x) = 1 (5 − x) (5 + x)
⇒ 60 + 12x − 60 + 12x = 25 − x2
⇒ 24x = 25 − x2
⇒ x2 + 24x − 25 = 0
⇒ x2 + 25x − x − 25 = 0
⇒ x (x + 25) − 1 (x + 25) = 0
⇒ (x − 1) (x − 25) = 0Either x − 1 = 0 ⇒ x = 1
or x + 25 = 0 ⇒ x = − 25
But x = − 25 is not admissible, because the speed of the stream cannot be negative∴ x = 1
⇒ speed of the stream = 1 km/hr.
Q7: The sum of the areas of two squares is 260 m2. If the difference of their perimeters is 24 m, then find the sides of the two squares.
Let the side of one of the squares be ‘x’ metres
∴ Perimeter of square-I = 4 × x metres = 4x metres
∴ Perimeter of square-II = (24 + 4x) metres
∴ Side of the square-IImetres
= (6 + x) metresNow, according to the condition, we have:
x2 + (6 + x)2 = 260
⇒x2 + 36 + x2 + 12x − 260 = 0
⇒ 2x2 + 12x − 224 = 0
⇒ x2 + 6x − 112 = 0 ...(1)Comparing (1) with ax2 + bx + c = 0, we get,
a = 1
b = 6
c = − 112∴ b2 − 4ac = (6)2 − 4 (1) (− 112)
= 36 + 448 = 484
∴
⇒
Taking +ve sign, we have
Taking −ve sign, we have
But x = − 14 is not required, as the length of a side cannot be negative.
∴ x = 8
⇒ Side of square-I = 8 m
⇒ Side of square-II = 6 + 8 m = 14 m.
Q8: The age of a father is twice the square of the age of his son. Eight years hence, the age of the father will be 4 years more than three times the age of his son. Find their present ages.
Let the present of son be ‘x’ years.
∴ Father’s present age = 2x2 years 8 years hence:Age of son = (x + 8) years
Age of father = (2x2 + 8) yearsAccording to the condition:
(2x2 + 8) = 3 (x + 8) + 4
⇒ 2x2 + 8 − 3x − 24 − 4= 0
⇒ 2x2 − 3x + 8 − 28 = 0
⇒ 2x2 − 3x − 20 = 0 ...(1)Comparing (1) with ax2 + bx + c = 0, we get
a = 2
b = −3
c = −20∴ b2 − 4ac =(− 3)2 − 4 (2) (− 20)
= 9 + 160 = 169
But x = -15/2 is not required, as the agecannot be negative.
∴ x = 4
⇒ Present age of son = 4 years
Present age of father = 2 × 42 = 32 years.
Q9: A motorboat whose speed in still water is 16 km/h, takes 2 hours more to go 60 km upstream than to return to the same spot. Find the speed of the stream.
Let the speed of the stream = x km/hr For the motor boat, we have:
∴Downstream speed = (16 + x) km/hr
Upstream speed = (16 − x) km/hr
For going 60 km:
According to the condition:
⇒ 60 (16 + x) − 60 (16 − x) = 2 (16 − x) (16 + x)
⇒ 960 + 60x − 960 + 60x = 2 (256 − x2)
⇒ 2x2 + 120x = 2 × 256 −2x2
⇒ x2 + 60x = 256
⇒ x2 + 60x − 250 = 0 ...(1)Comparing (1) with ax2 + bx + c = 0,
a = 1
b = 60
c = − 256∴ b2 − 4ac = (60)2 − 4 (1) (− 256)
1 = 3600 + 1024 = 4624
∴
⇒
⇒Taking +ve sign,
Taking −ve sign,
Since, the speed of a stream cannot be negative,
∴x = − 64 is not admissible
∴ x = 4
⇒ speed of the stream = 4 km/hr.
Q10: A train travels 288 km at a uniform speed. If the speed had been 4 km/hr more, it would have taken 1 hour less for the same journey. Find the speed of the train.
Let the speed of the train be x km/hr
∵ Total distance travelled = 288 km
In the other case, Speed of the train = (x + 4) km/hr
According to the condition,⇒ 288x + 1152 − 288x = 1 (x) (x + 4)
⇒ 288x + 1152 − 288x = x2 + 4x
⇒ 1152 = x2 + 4x
⇒ x2 + 4x − 1152 = 0 ...(1)Comparing (1) with ax2 + bx + c = 0,
a = 1
b = 4
c = − 1152∴ b2 − 4ac = (4)2 − 4 (1) (− 1152) = 16 + 4608
⇒
⇒Taking +ve sign,
Taking −ve sign,
∵ speed cannot be negative,
∴ x ≠− 36
∴ x = 32
⇒ speed of the train = 32 km/hr.
Q11: A train travels at a certain average speed for a distance of 63 km and then travels a distance of 72 km at an average speed of 6 km/hr more than its original speed. If takes 3 hours to complete the total journey, what is its original average speed?
Let the original average speed = x km/hr
∴ Time taken to cover 72 km = 72/ x + 6 hoursTime taken to cover 63 km = 63/x hours
Since, total time = 3 hours
∴
⇒
⇒
⇒
⇒
⇒ 3[15x + 42] = x2 + 6x⇒ 45x + 126 – x2 – 6x = 0
⇒ x2 – 39x – 126 = 0
⇒ x2 – 42x + 3x – 126 = 0
⇒ x(x – 42) + 3(x – 42) = 0
⇒ (x + 3) (x – 42) = 0Either x + 3 = 0 ⇒ x = – 3
or
x – 42 = 0 ⇒ x = 42
Since, speed cannot be negative,
∴ x = –3 is not desired.
Thus, the original speed of the train is 42 km/hr.
Q12: If − 5 is a root of the quadratic equation 2x2 + px − 15 = 0 and the quadratic equation p (x2 + x) + k = 0 has equal roots, then find the values of p and k.
Since − 5 is a root of 2x2 + px − 15 = 0,
∴ Substituting x = − 5 in the given equation, we get
2 (− 5)2 + p (− 5) − 15 = 0
⇒ 2 (25) + (− 5p) − 15 = 0
⇒ 50 − 5p − 15 = 0
⇒ − 5p + 35 = 0
⇒ − 5p = − 35⇒
Now, comparing the another quadratic equation p (x2 + x) + k = 0, i.e., px2 + px + k = 0 with ax2 + bx + c = 0, we have:
a = p
b = p
c = k
b2 − 4ac = p2 − 4 (p) (k)
= p2 − 4pkSince p (x2 − x) + k = 0 has equal roots,
∴ p2 − 4pk =0
⇒ (7)2 − 4 (7) k = 0 |∵ p = 7
⇒ 49 − 28k = 0
⇒
Thus, the required values of p = 7 and k = 7/4.
Q13: In a class test, the sum of Gagan’s marks in Mathematics and English is 45. If he had 1 more mark in Mathematics and 1 less in English, the product of marks would have been 500. Find the original marks obtained by Gagan in Mathematics and English separately.
Let Gagan’s marks in maths = x and Marks in English = (45 − x)
∴ According to the condition, (x + 1) × (45 − x + 1) = 500
⇒ (x + 1) × (44 − x) = 500
⇒ 44x − x2 + 44 − x = 500
⇒− x2 + 44x − 456 − x =0
⇒ x2 − 43x + 456 = 0
⇒ x2 − 19x − 24x + 456 = 0⇒ x (x − 19) − 24 (x − 19) = 0
⇒ (x − 19) (x − 24) = 0Either x − 19 = 0 ⇒ x = 19
or x − 24 = 0 ⇒ x = 24
When x = 19, then 45 − 19 = 26
When x = 24, then 45 − 24 = 21
∴ Gagan’s marks in Maths = 19 and in English = 26Or
Gagan’s marks in Maths = 24 and in English = 21.
Q14: The sum of areas of two squares is 640 m2. If the difference of their perimeters is 64 m, find the sides of two squares.
Let the side of square I be x metres.
∴ The perimeter of square I = 4x metres
⇒ Perimeter of square II = (64 + 4x) m
= (16 + x) mNow Area of square I = x × x = x2
Area of square II = (16 + x) × (16 + x) = (16 + x)2
= 256 + x2 + 32x
According to the condition, (x + 1) × (45 − x + 1) = 500
⇒ x2 + [256 + x2 + 32x] = 640
⇒ x2 + x2 + 32x + 256 − 640 = 0
⇒ 2x2 + 32x − 384 = 0
⇒ x2 + 16x − 192 = 0
⇒ x2 + 24x − 8x − 192 = 0⇒ x (x + 24) − 8 (x + 24) = 0
⇒(x + 24) (x − 8) = 0
Either x + 24 =0
⇒ x = − 24 or x − 8 = 0 ⇒ x = + 8∵ side of a square cannot be negative,
∴ Rejecting x = − 24, we have x = 8
⇒ Side of smaller square = 8 m
Side of larger square = 8 + 16 m = 24 m.
Q15: In a class test, the sum of Kamal’s marks in Mathematics and English is 40. Had he got 3 marks more in Mathematics and 4 marks less in English, the product of his marks would have been 360. Find his marks in two subjects separately.
Let Kamal’s marks in Maths = x
∴ His marks in English = (40 − x) According to the condition,(x + 3) [40 − x − 4] = 360
⇒ (x + 3) (36 − x) = 360
⇒ 36x − x2 + 108 − 3x − 360 = 0
⇒ − x2 + 33x − 252 = 0
⇒ x2 − 33x + 252 = 0
⇒ x2 − 21x − 12x + 252 = 0⇒ x (x − 21) − 12 (x − 21) = 0
⇒(x − 21) (x − 12) = 0
Either (x − 21) = 0
⇒ x = 21 = 0
or (x − 12) = 0
⇒ x = 12
For x = 21, Marks of Kamalin Maths = 21
in English = 40 − 21 = 19For x = 12, Marks of Kamal
in Maths = 12
in English = 40 − 12 = 28.
Q16: Solve the quadratic equation 2x2 + ax – a2 = 0
2x2 + ax – a2 =0
⇒ 2x2 + 2ax – ax – a2 =0
⇒ 2x[x + a] – a[x + a]=0⇒ (x + a) (2x – a) = 0
x = –a or x = a/2
|
126 videos|457 docs|75 tests
|
FAQs on Class 10 Maths Chapter 4 Question Answers - Quadratic Equations
| 1. What is a quadratic equation? |  |
| 2. How do you solve a quadratic equation using the quadratic formula? |  |
| 3. What are the different methods to solve quadratic equations? |  |
| 4. How can quadratic equations be applied in real-life situations? |  |
| 5. What is the discriminant of a quadratic equation? How does it determine the nature of solutions? |  |

|
Explore Courses for Class 10 exam
|

|
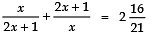
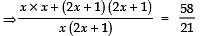
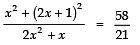
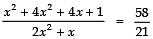

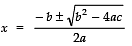
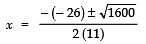
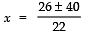
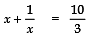
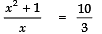


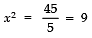
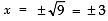
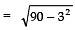
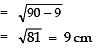
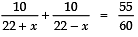
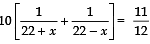

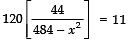
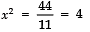
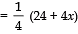 metres
metres