Class 9 Maths Chapter 10 Practice Question Answers - Circles
Q1. In the figure, OD is perpendicular to chord AB of a circle whose centre is O. If BC is a diameter, prove that CA = 2OD.
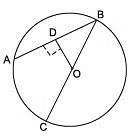 Solution: Given: BC is a diameter of a circle with centre O and OD⊥AB.
Solution: Given: BC is a diameter of a circle with centre O and OD⊥AB.
To prove: AC parallel to OD and AC = 2 × OD
Construction: Join AC.
Proof: We know that the perpendicular from the centre of a circle to a chord bisects the chord.
Here, OD⊥AB
D is the mid point of AB.
i.e., AD=BD
Also, O is the mid point of BC
.i.e., OC=OB
Now, in ΔABC, we have:
D is the mid point of AB and O is the mid point of BC.
According to the mid point theorem, the line segment joining the mid points of any two sides of a triangle is parallel to the third side and equal to half of it.
i.e., OD∥AC and OD=1/2AC
⇒ AC=2×OD
Hence, proved.
Q2. l is a line intersecting two concentric circles having common centre O, at A, B, C and D. Prove that AB = CD.
Solution:
Given: A line intersects two concentric circles (circles with the same center) with center O at A, B, C, and D
To prove: AB = CD
Construction: Draw OM ⊥ BC.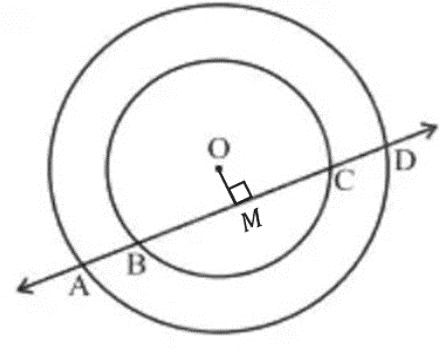
Proof: The perpendicular drawn from the centre of a circle to a chord bisects the chord.
AM = DM ---(1)
BM = CM -----(2)
Subtracting (2) from (1), we get
AM - BM = DM - CM
⇒ AB = CD
Hence Proved
Q3. AB and CD are equal chords of a circle whose centre is O. When produced, these chords meet at E. Prove that EB = ED.

Solution: From O draw OP⊥AB and OQ⊥CD. Join OE.
Given, AB = CD.
Since equal chords of a circle are equidistant from the centre, OP = OQ.
Now, in right triangles OPE and OQE,
OE = OE (common)
OP = OQ (proved above)
⟹△OPE≅△OQE (R.H.S.)
∴ PE = QE (C.P.C.T.)
⟹ PE−1/2AB=QE−1/2CD(because AB=CD (given))
⟹PE−PB=QE −QD
⟹EB=ED
⟹BE+AB=ED+CD (∵ AB=CD)
⟹AE =CE
Hence the given statement is true.
Q4. If O be the centre of the circle, find the value of ‘x’ in each of the following figures.


Solution:
(i) ∵ OA = OB [Radii of the same circle]
∴ ∠A = ∠B [Angles opposite to equal side in a triangle are equal]
In ΔABC, ∠A + ∠B + ∠O = 180º
∴ x + x + 70º = 180º [∵ ∠O = 70º (given) and ∠A = ∠B]
⇒ 2x + 70º = 180º
⇒ 2x = 180º - 70º = 110º
⇒ x= (1100/2)= 55º
Thus, x = 55°
(ii) In ΔAOC, ∠A + ∠ACO + ∠AOC = 180º
⇒ 40º + ∠ACO + 90º = 180º
⇒ ∠ACO = 180º - 40º - 90º = 50º
∵ AB is a diameter.
∴ ∠ACB = 90º [Angle in a semicircle]
∴ 50º + x = 90º
⇒ xº = 90º - 50º = 40º
Thus, x = 40º
(iii) ∵ ∠AOC + ∠COB = 180º [Linear pairs]
∴ 120º + ∠COB = 180º
⇒ ∠COB = 180º - 120º = 60º
∵ The arc CB is subtending ∠COB at the centre and ∠CDB at the remaining part.
∴ ∠CDB = (1/2)∠COB
⇒ x= (1/2)(60º) = 30º
⇒ x = 30º
(iv) In ΔAOC,
∵ AO = OC [Radii of the same circle]
∴ ∠OAC = ∠OCA [Angles opposite to equal sides are equal]
⇒ ∠OAC = 50º
∴ Exterior ∠COB = 50º + 50º = 100º.
Now, the arc BC is subtending ∠BOC at the centre and ∠BDC at the remaining part of the circle.
∴ ∠BDC = (1/2)∠BOC
⇒ x= (1/2)(100º) = 50º
Thus, x = 50º
(v) In ΔOAC, OA = OC [Radii of the same circle]
∴ ∠AOC = ∠ACO [∵ Angles opposite to equal sides are equal]
Now, ∠AOC + ∠ACO + ∠OAC = 180º
⇒ ∠AOC + ∠ACO + 50º = 180º
⇒ ∠AOC + ∠ACO = 180º - 50º = 130º
⇒ ∠AOC = ∠ACO = (1300/2) = 65º
Now, ∠AOB + ∠AOC = 180º [Linear pairs]
∴ ∠AOB + 65º = 180º
⇒ ∠AOB = 180º - 65º = 125º
∵ The arc AB subtends ∠AOB at the centre and ∠ADB at the remaining part of the circle.
∴ ∠ADB = (1/2) ∠AOB
⇒ x= (1/2)(125º) = 62 (1/2)
∴ x= 62(1/2)º
(vi) ∵ ∠BDC = ∠BAC [Angles in the same segment]
∴ ∠BDC = 40º
Now, in ΔBDC, we have ∠BDC + ∠CBD + ∠BCD = 180º
∴ 40º + 80º + x = 180º
⇒ 120º + x = 180º
⇒ x = 180º - 120º = 60º
Thus, x = 60º
Q5. In the adjoining figure, O is the centre of the circle. Prove that ∠ XOZ = 2(∠ XZY + ∠ YXZ).
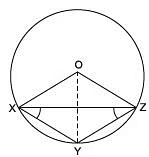 Solution: Let us join OY.
Solution: Let us join OY.
∵ The arc XY subtends ∠XOY at the centre and ∠XZY at a point Z on the remaining part of the circle.

∴ ∠XOY = 2∠XZY …(1)
Similarly, ∠YOZ = 2∠YXZ …(2)
Adding (1) and (2), we have ∠XOY + ∠YOZ = 2∠XZY + 2∠YXZ
⇒ ∠XOZ = 2[∠XZY + ∠YXZ]
Q6. Show that the sum of the opposite angles of a cyclic quadrilateral is 180º.
Solution: We have a cyclic quadrilateral. Let us join AC and BD. Since, angles in the same segment are equal.
∴ ∠ACB = ∠ADB …(1)
and ∠BAC = ∠BDC …(2)
Adding (1) and (2), we have

∠ACB + ∠BAC = ∠ADB + ∠BDC
⇒ ∠ACB + ∠BAC = ∠ADC
Adding ∠ABC to both sides, we have ∠ACB + ∠BAC + ∠ABC = ∠ADC + ∠ABC
But, ∠ACB + ∠BAC + ∠ABC = 180º [Sum of the angles of ΔABC = 180º]
∴ ∠ADC + ∠ABC = 180º
⇒ ∠B + ∠D = 180º
Since, ∠A + ∠B + ∠C + ∠D = 360º
⇒ ∠A + ∠C = 360º ∠ 180º = 180º

Q7. Prove that the quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic.
Solution: We have a cyclic quadrilateral ABCD in which the bisectors ∠A, ∠B, ∠C and ∠D for a quadrilateral PQRS.
From ΔABP, we have ∠PAB + ∠PBA + ∠P = 180º [Sum of the three angles of ΔABP]
 ⇒ (1/2) ∠A + (1/2)∠B + ∠P = 180º …(1)
⇒ (1/2) ∠A + (1/2)∠B + ∠P = 180º …(1)
From ΔCDR, we have
∠RCD + ∠RDC + ∠R = 180º [Sum of the three angles of ΔCDR.]
⇒ (1/2)∠C +(1/2)∠D + ∠R = 180° …(2)
Adding (1) and (2), we have (1/2)∠A + (1/2)∠B + (1/2)∠C +(1/2)∠D + ∠P + ∠R = 360º
⇒ (1/2) (∠A + ∠B + ∠C + ∠D) + ∠P + ∠R = 360º
⇒ (1/2)(360º) + ∠P + ∠R = 360º [∵ ∠A + ∠B + ∠C + ∠D = 360°]
⇒ ∠P + ∠R = 360º -(1/2) (360º) = 180º
Similarly, ∠Q + ∠S = 180º
Thus, the pairs of opposite angles of quadrilateral PQRS are supplementary.
Hence, PQRS is cyclic.
Q8. ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.

Solution: Consider the chord CD,
As we know, angles in the same segment are equal.
So, ∠CBD = ∠CAD
∴ ∠CAD = 70°
Now, ∠BAD will be equal to the sum of angles BAC and CAD.
So, ∠BAD = ∠BAC + ∠CAD
= 30° + 70°
∴ ∠BAD = 100°
As we know, the opposite angles of a cyclic quadrilateral sum up to 180 degrees.
So,
∠BCD + ∠BAD = 180°
Since, ∠BAD = 100°
So, ∠BCD = 80°
Now consider the ΔABC.
Here, it is given that AB = BC
Also, ∠BCA = ∠CAB (Angles opposite to equal sides of a triangle)
∠BCA = 30°
also, ∠BCD = 80°
∠BCA + ∠ACD = 80°
So, ∠ACD = 50° and,
∠ECD = 50°
Q9. In Figure, ∠ABC = 69°, ∠ ACB = 31°, find ∠BDC.
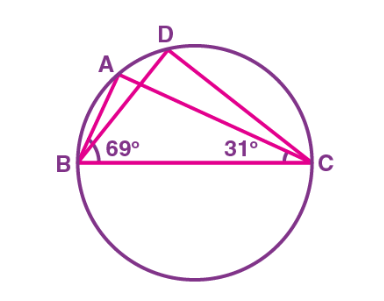
Solution: As we know, angles in the segment of the circle are equal so,
∠BAC = ∠BDC
Now in the In ΔABC, sum of all the interior angles will be 180°
So, ∠ABC + ∠BAC + ∠ACB = 180°
Now, by putting the values,
∠BAC = 180° – 69° – 31°
So, ∠BAC = 80°
Q10. Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
Solution:

Here, it is given that ∠AOB = ∠COD i.e. they are equal angles.
Now, we will have to prove that the line segments AB and CD are equal i.e. AB = CD.
Proof:
In triangles AOB and COD,
∠AOB = ∠COD (as given in the question)
OA = OC and OB = OD ((these are the radii of the circle)
So, by SAS congruency, ΔAOB ≅ ΔCOD.
∴ By the rule of CPCT, AB = CD. (Hence proved).
|
44 videos|412 docs|54 tests
|
FAQs on Class 9 Maths Chapter 10 Practice Question Answers - Circles
| 1. What are the basic properties of circles that I should know? |  |
| 2. How do you calculate the circumference of a circle? |  |
| 3. What is the difference between a chord and a diameter? |  |
| 4. Can you explain what a tangent to a circle is? |  |
| 5. How do you find the area of a circle given its radius? |  |

|
Explore Courses for Class 9 exam
|

|

















