Class 9 Maths Question Answers - Herons Formula
Q1.Find the area of a triangle whose sides are 5 cm, 6 cm, and 7 cm.
Sol:
s = 5 + 6 + 72 = 9 cm.
Heron's formula for the area of the triangle:
Area = √s(s − 5)(s − 6)(s − 7) cm2
Area = √(9)(9 − 5)(9 − 6)(9 − 7) cm2
Area = √(9 × 4 × 3 × 2) cm2
Area = √216 cm2
Area = 14.7 cm2
Q2. Find the area of a triangle whose sides are 3 cm, 4 cm and 5 cm.
Sol:
s = 3 + 4 + 52 = 6 cm
Heron's formula for the area of the triangle:
Area = √s(s − 3)(s − 4)(s − 5) cm2
Area = √(6)(6 − 3)(6 − 4)(6 − 5) = √(6 × 3 × 2 × 1)
Area = √36 cm2
The area of the triangle is 6 cm2.
Q3. Find the area of a triangle whose two sides are 18 cm and 10 cm and the perimeter is 42cm.
Sol: Assume that the third side of the triangle to be “x”.
Now, the three sides of the triangle are 18 cm, 10 cm, and “x” cm
It is given that the perimeter of the triangle = 42cm
So, x = 42 – (18 + 10) cm = 14 cm
∴ The semi perimeter of triangle = 42/2 = 21 cm
Using Heron’s formula,
Area of the triangle,
= √[s (s-a) (s-b) (s-c)]
= √[21(21 – 18) (21 – 10) (21 – 14)] cm2
= √[21 × 3 × 11 × 7] m2
= 21√11 cm2
Q4.If the perimeter of an equilateral triangle is 180 cm. Then its area will be ?
Solution. Given, Perimeter = 180 cm
3a = 180 (Equilateral triangle)
a = 60 cm
Semi-perimeter = 180/2 = 90 cm
Now as per Heron’s formula,
= √s (s-a)(s-b)(s-c)
In the case of an equilateral triangle, a = b = c = 60 cmSubstituting these values in the Heron’s formula, we get the area of the triangle as:
A = √[90(90 – 60)(90 – 60)(90 – 60)]
= √(90× 30 × 30 × 30)
A = 900√3 cm2
Q5.The sides of a triangle are 122 m, 22 m and 120 m respectively. The area of the triangle is ?
Sol: Given,
a = 122 m
b = 22 m
c = 120 m
Semi-perimeter, s = (122 + 22 + 120)/2 = 132 m
Using heron’s formula:
= √s (s-a)(s-b)(s-c)
= √[132(132 – 122)(132 – 22)(132 – 120)]
= √(132 × 10 × 110 × 12)
= 1320 sq.m
Q6. The sides of a triangle are in the ratio 12: 17: 25 and its perimeter is 540 cm. The area is:
Sol: The ratio of the sides is 12: 17: 25
Perimeter = 540 cm
Let the sides of the triangle be 12x, 17x and 25x.
Hence,
12x + 17x + 25x = 540 cm
54x = 540 cm
x = 10
Therefore,
a = 12x = 12 × 10 = 120
b = 17x = 17 × 10 = 170
c = 25x = 25 × 10 = 250
Semi-perimeter, s = 540/2 = 270 cm
Using Heron’s formula:
= √[270(270 – 120)(270 – 170)(270 – 250)]
= √(270 × 150 × 100 × 20)
= 9000 sq.cm
Q7. Find the area of an equilateral triangle having side length equal to √3/4 cm (using Heron’s formula)
Sol: Here, a = b = c = √3/4
Semiperimeter = (a + b + c)/2 = 3a/2 = 3√3/8 cm
Using Heron’s formula,
= √[(3√3/8) (3√3/8 – √3/4)(3√3/8 – √3/4)(3√3/8 – √3/4)]
= 3√3/64 sq.cm
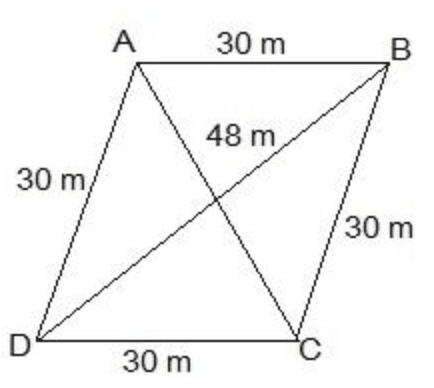
Q8. A rhombus-shaped field has green grass for 18 cows to graze. If each side of the rhombus is 30 m and its longer diagonal is 48 m, how much area of grass field will each cow be getting?
Sol: Draw a rhombus-shaped field first with the vertices as ABCD. The diagonal AC divides the rhombus into two congruent triangles which are having equal areas. The diagram is as follows.
Consider the triangle BCD,
Its semi-perimeter = (48 + 30 + 30)/2 m = 54 m
Using Heron’s formula,
Area of the ΔBCD =
Area = √[s(s − a)(s − b)(s − c)]
= √[54(54 − 48)(54 − 30)(54 − 30)] m2
= √[54 × 6 × 24 × 24] m2
= 432 m2
∴ Area of field = 2 × area of the ΔBCD = (2 × 432) m2 = 864 m2
Thus, the area of the grass field that each cow will be getting = (864/18) m2 = 48 m2
Q9. The area of an isosceles triangle having a base 2 cm and the length of one of the equal sides 4 cm, is
Solution: Given that a = 2 cm, b= c = 4 cm
s = (2 + 4 + 4)/2 = 10/2 = 5 cm
By using Heron’s formula, we get:
A =√[5(5 – 2)(5 – 4)(5 – 4)] = √[(5)(3)(1)(1)] = √15 cm2.
Q10. The perimeter of an equilateral triangle is 60 m. The area is
Solution:
Given: Perimeter of an equilateral triangle = 60 m
3a = 60 m (As the perimeter of an equilateral triangle is 3a units)
a = 20 cm.
We know that area of equilateral triangle = (√3/4)a2square units
A = (√3/4)202
A = (√3/4)(400) = 100√3 m2.
|
40 videos|471 docs|57 tests
|
FAQs on Class 9 Maths Question Answers - Herons Formula
| 1. What is Heron’s Formula used for? |  |
| 2. How do you calculate the semi-perimeter in Heron’s Formula? |  |
| 3. What is the formula for the area of a triangle using Heron’s Formula? |  |
| 4. Can Heron’s Formula be used for all types of triangles? |  |
| 5. What conditions must be met for using Heron’s Formula? |  |