Class 9 Maths Chapter 10 Question Answers - Heron’s Formula
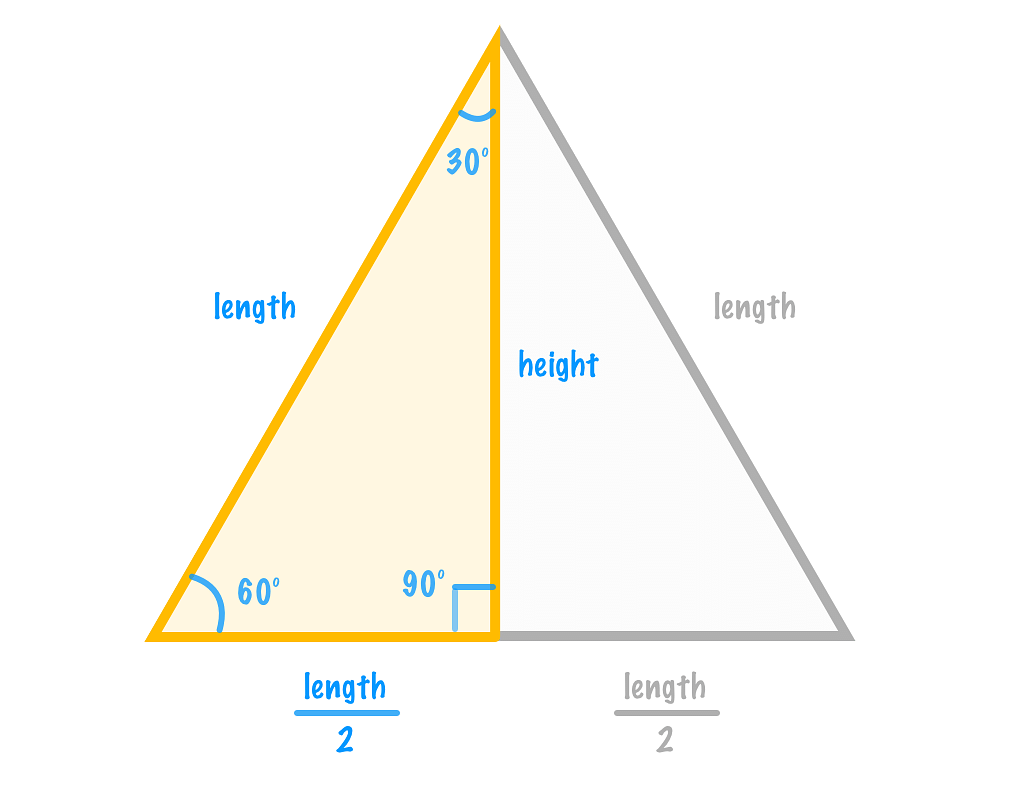
Q1. The area of an equilateral triangle whose side is ‘a’ cm is (√3/4)a2 cm2. Find its height.
Area of the triangle = (√3/4)a2 cm2
∵ Area of a triangle = (1/2)x base x height
∴ (1/2) x a x height =(√3/4)x a2
⇒ height =(√3/4) a2 x (2/a) = (√3/2) a cm
Q2. Find the height of an equilateral triangle whose side is 2 cm.
Since height of an equilateral triangle is given by
height = (√3/2) x side
⇒ height =(√3/2) x 2 cm = √3 cm
Q3. Find the length of a diagonal of a square whose side is 2 cm.
The diagonal of a square = (√2) a cm
∴ Length of the diagonal = (√2) x 2 cm = 2√2cm.
Q4. The diagonal of a square is 9√2 cm. What is the side?
Let side of the square = x cm.
∵ Its diagonal is given by √2 x side.
∴ √2 x x= 9 x √2⇒
Thus, the required length of sides of the square is 9 cm.
Q5. The length of a rectangular plot of land is twice its breadth. If the perimeter of the plot be 180 metres, then find its area.
Let the breadth of the plot be ‘x’ metres.
∴ Its length = 2x metres
Since perimeter of a rectangular plot = 2[Length + Breadth]
∴ Perimeter of the given plot = 2[x + 2x]
= 2[3x]
= 6x metres
⇒ 6x = 180
⇒ x= 180/6= 30 metres
⇒ 2x = 2 x 30 = 60 metres.
∴ Length of the plot = 60 metres and Breadth of the plot = 30 meters.
∴ Area of the plot = Length x Breadth = 60 x 30 m2 = 1800 m2
Q6. The length of the sides containing the right angle in a right triangle differ by 7 cm. The area of the triangle is 60 cm2. Find the length of the hypotenuse.
Let the sides containing the right angle be ‘x’ cm and (x – 7) cm.
i.e. Base = x cm and height = (x – 7) cm
∴ Area = (1/2) x base x height=(1/2) x x x (x – 7) cm2
Now (1/2) x (x – 7) = 60
⇒ x(x – 7) = 120
⇒ x2 – 7x – 120 = 0
⇒ x2 – 15x + 8x – 120 = 0
⇒ x(x – 15) + 8(x – 15) = 0
⇒ (x + 8)(x – 15) = 0
⇒ x = – 8 or x = 15
Rejecting x = –8, we have x – 15 = 0
⇒ x = 15 cm x – 7 = 15 – 7 = 8 cm
Now, Hypotenuse= √289 = 17cm
Thus, the required length of the hypotenuse is 17 cm.
Q7. The lengths of sides of a triangle are in the ratio 3 : 4 : 5 and its perimeter is 120 cm, find its area.
The sides are in the ratio of 3 : 4 : 5.
Let the sides be 3x, 4x and 5x.
∴ Perimeter = 3x + 4x + 5x = 12x
Now 12x = 120 [Perimeter = 120 cm]
⇒ x =(120/12) = 10
∴ Lengths are: a = 3x = 3 x 10 = 30 cm
b = 4x = 4 x 10 = 40 cm
c = 5x = 5 x 10 = 50 cm
Now, semi-perimeter (s) = (120/12)
cm = 60 cm
∵ (s – a) = 60 – 30 = 30 cm
(s – b) = 60 – 40 = 20 cm
(s – c) = 60 – 50 = 10 cmUsing Heron’s formula, we have
Area of the triangle =
= 2 x 30 x 10 cm2 = 600 cm2 Thus, the required area of the triangle = 600 cm2.
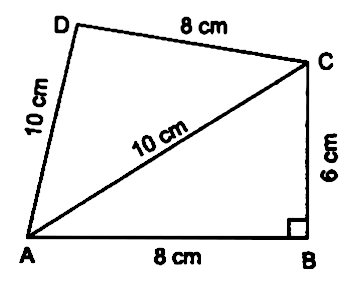
Q8. Find the area of a quadrilateral ABCD in which AB = 8 cm, BC = 6 cm, CD = 8 cm, DA = 10 cm and AC = 10 cm.
In ΔABC, ∠B = 90°
∴ area of right (rt ΔABC) = (1/2) x 8 x 6 cm2 = 24 cm2
In ΔACD,
a = AC = 10 cm b = AD = 10 cm c = CD = 8 cm
∴Area of ΔACD
= 2 x 4√21 = 8√21 cm2
= 8 x 4,58 cm2 = 36.64 cm2
Now, area of quadrilateral ABCD = ar (ΔABC) + ar (ΔACD)
= 24 cm2 + 8√21 cm2
= 24 cm2 + 36.64 cm2
= 60.64 cm2
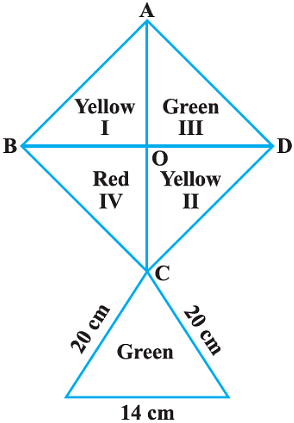
Q9. How much paper of each shade is needed to make a kite given in the figure, in which ABCD is a square of diagonal 44 cm.
∵ The diagonals of a square bisect each other at right angles
∴ OB = OD = OA = OC = (44/2) = 22 cm
Now, ar rt (Δ –I) = (1/2)× OB × OA
= (1/2) × 22 × 22 cm2 = 242 cm2
Similarly ar rt (Δ –II) = arrt(Δ–III) = ar rt (Δ –IV) = 242 cm2∵ Sides of ΔCEF are 20 cm, 20 cm and 14 cm
⇒ Area of ΔCEF
Now, area of yellow paper = ar (Δ – I) + ar (Δ – II)
= 242 cm2 + 242 cm2 = 484 cm2
Area of red paper = ar (Δ – IV) = 242 cm2
Area of green paper = ar (Δ – III) + ar ΔCEF
= 242 cm2 + 131.14 cm2
= 373.14 cm2
|
44 videos|412 docs|54 tests
|
FAQs on Class 9 Maths Chapter 10 Question Answers - Heron’s Formula
| 1. What is Heron’s Formula and how is it used to calculate the area of a triangle? |  |
| 2. How do you calculate the semi-perimeter in Heron’s Formula? |  |
| 3. Can Heron’s Formula be applied to any type of triangle? |  |
| 4. What are the limitations of using Heron’s Formula? |  |
| 5. How can Heron’s Formula be derived? |  |

|
Explore Courses for Class 9 exam
|

|
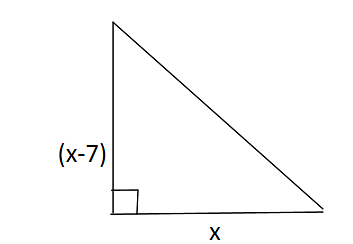 ∴ Area = (1/2) x base x height=(1/2) x x x (x – 7) cm2
∴ Area = (1/2) x base x height=(1/2) x x x (x – 7) cm2