Class 10 Maths Chapter 4 Question Answers - Quadratic Equations
Q1. Rahul plans to grow organic vegetables in a 100 sq. m rectangular plot. He has only 30 m of barbed wire which can fence its three sides. Fourth side of his plot touches Rehaman's compound wall. He requests Rehaman to allow his compound wall be used as fencing to his plot.
(a) Find the dimensions of the plot.
(b) Which mathematical concept is used in above problem?
(c) By allowing the compound wall to act as fencing, which value is depicted by Rehaman?

Sol. Let ‘x’ metres be the width and ‘y’ metres be the length of the vegetable plot.
∴ Area = xy sq. m
⇒ xy = 100 ... (i)
∴ length of the barbed wire = 30 m
x + y + y = 30 m
⇒ x + 2y =30
⇒ 

From (i) and (ii), we have

⇒ x2 – 30x + 200 = 0
⇒ (x – 10) (x – 20) = 0
⇒ x = 10 or x = 20

Thus,
(a) The dimensions of the plot are: 10m, 10m or 20m, 5m.
(b) Quadratic Equations
(c) Co-operation.
Q2. A shopkeeper buys a certain number of books from a publisher for Rs 80. The publisher gives him 4 more books for the same amount with a condition that the shopkeeper would donate ₹ 1 per book to an orphanage.
(a) How many books did he buy?
(b) Which mathematical concept is used in this problem?
(c) By allowing ₹ 1 per book towards an orphanage, which value is depicted by the publisher?
Sol. Let the number of books bought = x
∴ Cost of x books = Rs 80

Again,
Cost of (x + 4) books = Rs 80
Since the shopkeeper donates Rs 1 per book to an orphanage.
∴ 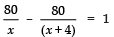
⇒ 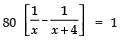
⇒ 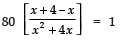
⇒ 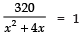
⇒ x2 + 4x = 320
⇒ x2 + 4x – 320 = 0
⇒ x2 + 20x – 16x – 320 = 0
⇒ x (x + 20) – 16 (x + 20) = 0
⇒ (x + 20) (x – 16) = 0
⇒ x = –20 or x = 16
∵ x cannot of negative
∴ x =16
Thus,
(a) Number of books bought = 16
(b) Quadratic Equations
(c) Charity
Q3. Radha wants to buy a piece of cloth for Rs 200. She bought another 5m piece of cloth for donation to a blind school. For this, the shopkeeper reduces the cost by Rs 2 per metre such that the total cost remains the same (Rs 200).
(a) What is the original rate per metre?
(b) Which mathematical concept is used in the above problem?
(c) By donating a piece of cloth to the blind school, which value is depicted?
Sol. Let the original length of cloth = ‘x’ metres

New length of the cloth = (x + 5) metres
The new length of cloth 
∴ The new rate is Rs 2 less than the original rate
∴ 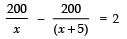
⇒ 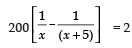
⇒ 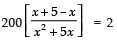
⇒ 1000 = 2 (x2 + 5x)
⇒ 1000 = 2x2 + 10x
⇒ x2 + 5x – 500 = 0
⇒ x2 + 25x – 20x – 500 = 0
⇒ (x + 25) (x – 20) = 0
⇒ x = –25, which is not desirable or x = 20 Now,
(a) Original rate  per metre
per metre
(b) Quadratic Equations
(c) Charity
Q4. Ranjeet wants to go by car from the place – ‘A’ to ‘B’. He has two options.
(i) He can go straight from A to B.
(ii) He goes to ‘C’ due east and then from ‘C’ to ‘B’ due north.
The distance between A to B exceeds the distance between A to C by 2 km. The distance between ‘A’ to ‘B’ exceeds twice the distance between ‘C’ and ‘B’ by 1 km.
He decided to choose option (i) for going from ‘A’ to ‘B’.
(a) Find the distance difference in the above two options.
(b) Which mathematical concept is used in the above problem?
(c) By choosing the option
(i), which value is depicted by Ranjeet?

Sol. Let the distance between ‘C’ and ‘B’ =x km
∴ Distance between ‘A’ and ‘B’ = (2 x +1) km And distance between ‘A’ and ‘C’
= (2x + 1) – 2 km
= (2x – 1) km
∴ The direction East and North are perpendicular to each other.
∴ AC ⊥ BC
⇒ ABC is a right angle Δ, right angled at C
∴ Using Pythagoras theorem, we have:
⇒ x2 + (2x – 1)2 = (2x + 1)2
⇒ x2 + 4x2 – 4x + 1 = 4x2 + 4x + 1
⇒ x2 – 8x = 0
⇒ x (x – 8) = 0
⇒ Either x = 0, [Which is not possible as distance cannot be zero]
Or x = 8

Now, AB = (2x + 1) km = (16 + 1) km = 17 km
AC = (2x – 1) km = (16 – 1) km = 15 km
BC = x km = 8 km
Now, (a) Difference in distance
= (AC + BC) – AB = (15 + 8) km – 17 km
= 23 km – 17 km = 6 km
(b) Quadratic Equations
(c) Saving of National resource (fuel consumption)
Q5. Three-eighth of the students of a class opted for visiting an old age home. Sixteen students opted for having a nature walk. The square root of the total number of students in the class opted for tree plantation in the school. The number of students who visited an old age home is the same as the number of students who went for a nature walk and did tree plantation. Find the total number of students. What values are inculcated in students through such activities?
Sol. Let the total number of students = x
Number of students visited old age home 
Number of students having a nature walk = 16
Number of students who opted for tree plantation = √x
According to the question, [Number of students visited old agehome] = [Number of students having nature walk] + [Number of students tree plantation]

Solving the above equation, we get x = 64
∴ Required number of students = 64
Values: (i) Helping the old age persons
(ii) Loving & protecting nature.
|
126 videos|457 docs|75 tests
|
FAQs on Class 10 Maths Chapter 4 Question Answers - Quadratic Equations
| 1. What is the importance of understanding quadratic equations? |  |
| 2. How can quadratic equations be applied in everyday life? |  |
| 3. How do quadratic equations help in solving problems related to motion and trajectory? |  |
| 4. What are the practical applications of quadratic equations? |  |
| 5. How can understanding quadratic equations help in making informed decisions? |  |

|
Explore Courses for Class 10 exam
|

|

















