NCERT Solutions for Class 9 Maths - Statistics (Exercise 12.1)
Q1. A survey conducted by an organisation for the cause of illness and death among the women between the ages 15–44 (in years) worldwide, found the following figures (in %):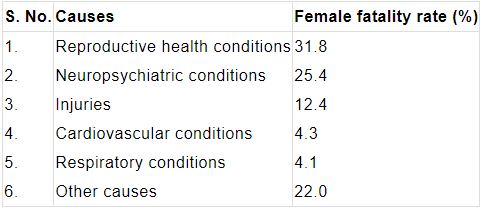
(i) Represent the information given above graphically.
(ii) Which condition is the major cause of women’s ill health and death worldwide?
(iii) Try to find out, with the help of your teacher, any two factors which play a major role in the cause in (ii) above being the major cause.
Ans: (i) The given data can be represented using a bar graph by depicting causes on the x-axis and family fatality rate on the y-axis, and selecting an acceptable scale (1 unit = 5% for the y-axis).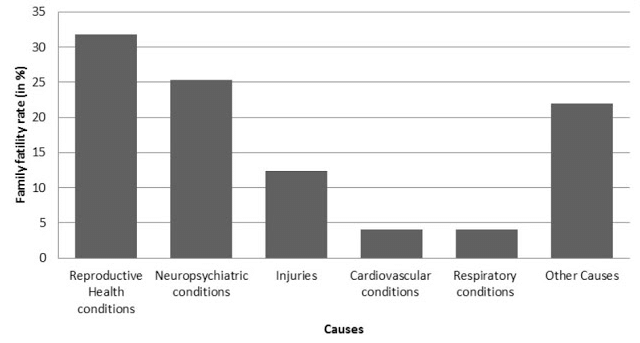
(ii) Reproductive health issues are the primary cause of women's illness and mortality worldwide, affecting 31.8% of women.
(iii) Two factors responsible for the cause in (ii) are:
- Lack of proper care and understanding.
- Lack of medical facilities.
Q2. The following data on the number of girls (to the nearest ten) per thousand boys in different sections of Indian society is given below.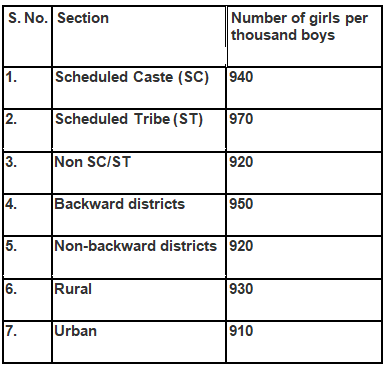
(i) Represent the above information by a bar graph.
(ii) In the classroom, discuss what conclusions can be arrived at from the graph.
Ans: (i) The graph of the information presented above may be built by choosing an appropriate scale (1 unit = 100 girls for the y-axis) and representing each section (variable) on the x-axis and the number of girls per thousand boys on the y-axis.
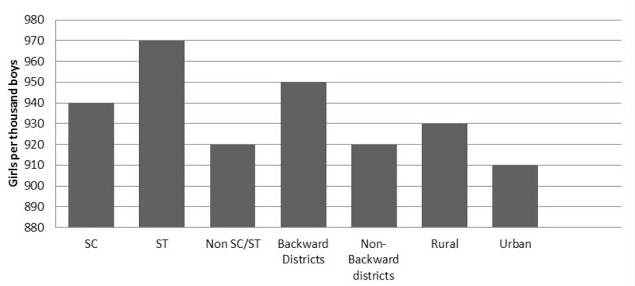 (ii) The graph indicates that the highest number of girls per thousand boys, which is 970, is found in the Scheduled Tribes (ST) category. Conversely, the lowest figure, 910, is observed in urban areas.
(ii) The graph indicates that the highest number of girls per thousand boys, which is 970, is found in the Scheduled Tribes (ST) category. Conversely, the lowest figure, 910, is observed in urban areas.
Furthermore, the data reveal that the number of girls per thousand boys is greater in rural regions compared to urban areas, in backward districts compared to non-backward districts, and in SC/ST districts compared to non-SC/ST ones.
Q3. Given below are the seats won by different political parties in the polling outcome of a state assembly elections: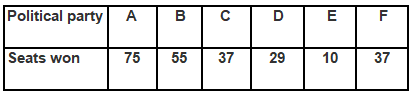
(i) Draw a bar graph to represent the polling results.
(ii) Which political party won the maximum number of seats?
Ans:
(i) The bar graph representing the polling results is given below: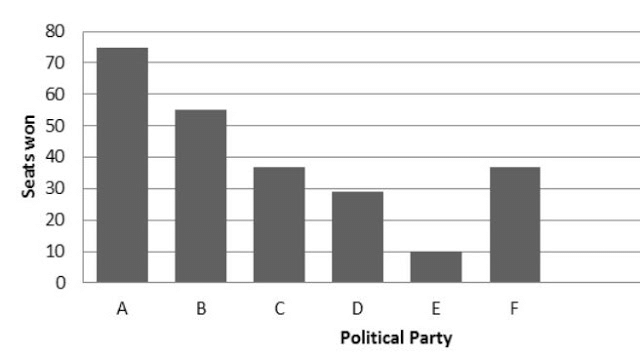
(ii) From the bar graph, it is clear that Party A won the maximum number of seats.
Q4. The length of 40 leaves of a plant are measured correct to one millimetre, and the obtained data is represented in the following table:
(i) Draw a histogram to represent the given data. [Hint: First make the class intervals continuous]
(ii) Is there any other suitable graphical representation for the same data?
(iii) Is it correct to conclude that the maximum number of leaves are 153 mm long? Why?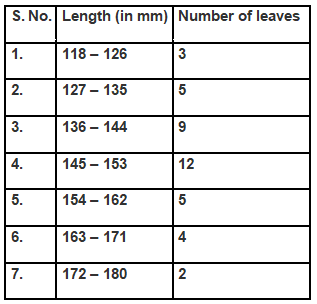
Ans: (i) The data provided in the question is represented in discontinuous class intervals. To convert it into continuous class intervals, we need to adjust the limits. Since the difference between the intervals is 1, we subtract 0.5 from the lower limit and add 0.5 to the upper limit. The revised class intervals are as follows: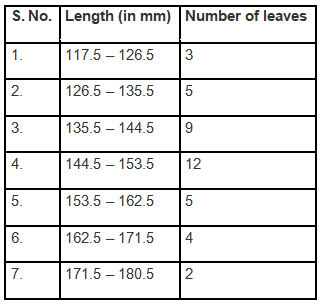
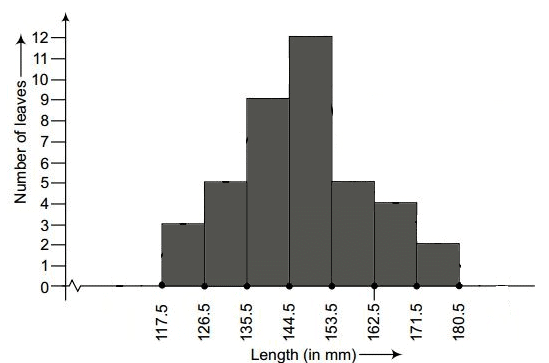 (ii) Yes, the data given in the question can also be represented by a frequency polygon.
(ii) Yes, the data given in the question can also be represented by a frequency polygon.
(iii) No, we cannot conclude that the maximum number of leaves is 153 mm long. The maximum number of leaves actually falls within the range of 144.5 mm to 153.5 mm.
Q5. The following table gives the life times of 400 neon lamps: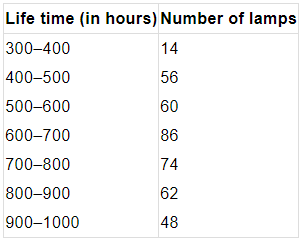
(i) Represent the given information with the help of a histogram.
(ii) How many lamps have a life time of more than 700 hours?
Ans:
(i) The histogram representation of the given data is given below:
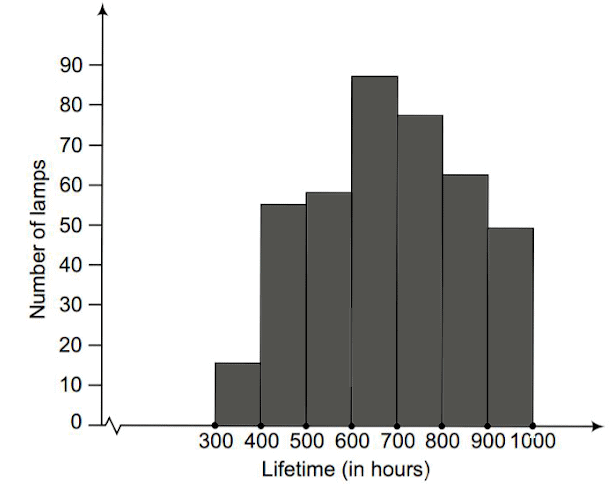
(ii) To find the number of neon lamps with a lifetime exceeding 700 hours, we can sum the quantities of lamps in the intervals of 700, 800, and 900 hours. So, 184 neon lamps have a lifetime of more than 700 hours (74 + 62 + 48 = 184).
Q6. The following table gives the distribution of students of two sections according to the marks obtained by them: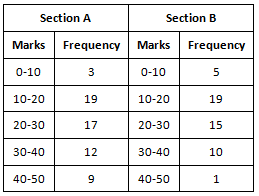
Represent the marks of the students of both sections on the same graph by two frequency polygons. From the two polygons compare the performance of the two sections.
Ans:
The class-marks = (lower limit + upper limit)/2
For section A: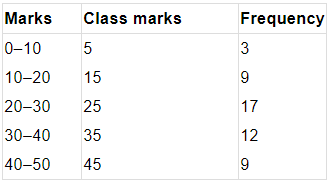
For section B:
By plotting these data points on a graph using two frequency polygons, we obtain the following representation: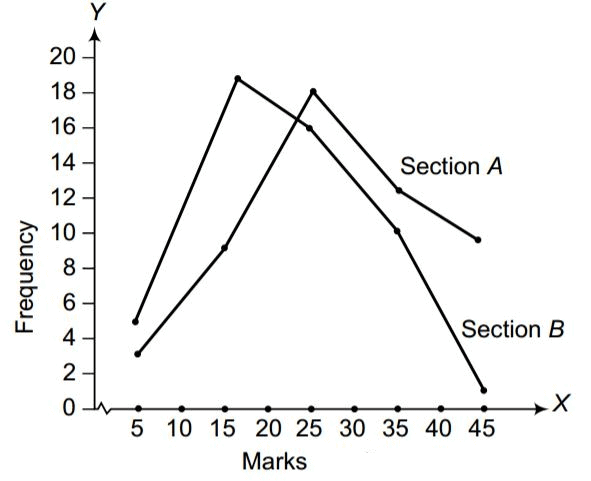
From the graph, it is evident that the students in Section A performed better than those in Section B.
Q7. The runs scored by two teams A and B on the first 60 balls in a cricket match are given below: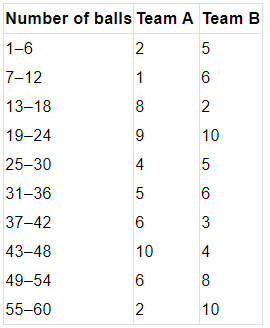
Represent the data of both teams on the same graph by frequency polygons.
Note: The given class intervals are not continuous. Therefore, we first modify the distribution to be continuous.
Ans: The data provided in the question is presented in discontinuous class intervals. To create continuous class intervals, we need to adjust the limits. Since the difference between the intervals is 1, we subtract 0.5 from the lower limit and add 0.5 to the upper limit. This adjustment results in the following table: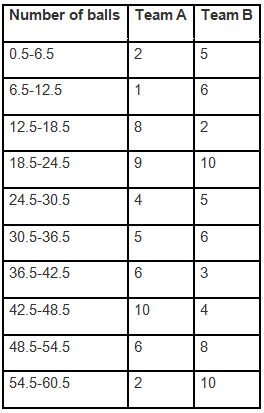
The runs scored by both teams are then represented on the graph below using frequency polygons.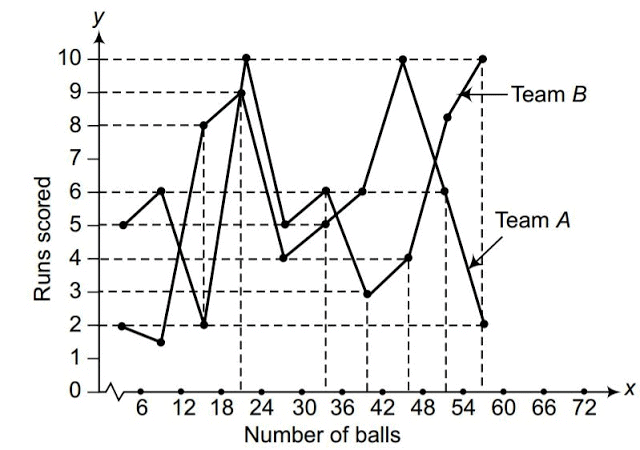
Q8. A random survey of the number of children of various age groups playing in a park was found as follows:
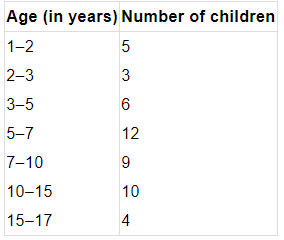 Draw a histogram to represent the above data.
Draw a histogram to represent the above data.
Ans: The width of the class intervals in the given data varies. It is important to note that the area of each rectangle in the histogram is proportional to the frequencies represented. Therefore, we can calculate the proportion of children per year as shown in the table below. To create the histogram, we will place the ages (in years) on the x-axis and the corresponding adjusted frequencies on the y-axis. The x-axis represents the age of the children, while the y-axis indicates the frequency density (proportion per year). Below is the graphical representation:
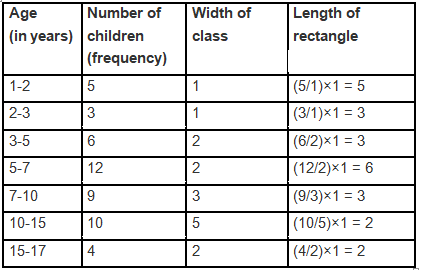 Let the x-axis = the age of children
Let the x-axis = the age of children
y-axis = proportion of children per 1-year interval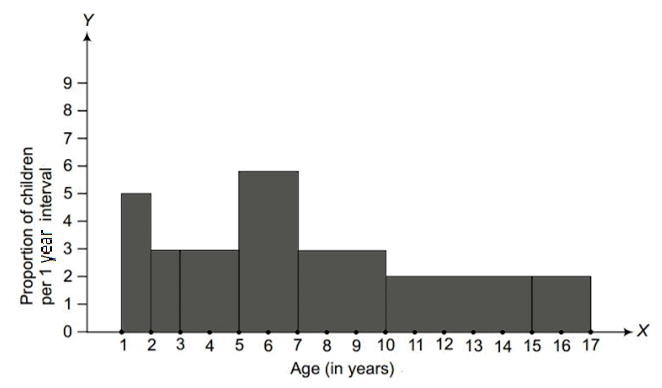
Q9. 100 surnames were randomly picked up from a local telephone directory and a frequency distribution of the number of letters in the English alphabet in the surnames was found as follows:

(i) Draw a histogram to depict the given information.
(ii) Write the class interval in which the maximum number of surnames lie.
Ans:
(i) The width of the class intervals in the provided data varies. The area of each rectangle in the histogram corresponds to the frequencies. Therefore, we can calculate the proportion of surnames for each 2-letter interval as shown in the table below.

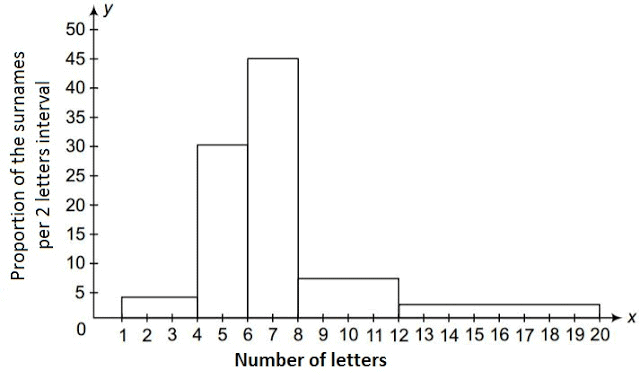
(ii) The class interval 6–8 contains the highest number of surnames.
MEASURES OF CENTRAL TENDENCY
- We can make out some important features of the given data by considering only certain representatives.
- These representatives are called the measures of central tendency or averages. There are three main averages: Mean, Median and Mode.
Mean
- The mean (or average) of a number of observations is the sum of the values of all the observations divided by the total number of observations.
- It is denoted by the symbol x, and we read it as x-bar.
Here ∑ is a Greek symbol called sigma.
The summation is read as the sum of x as i varies from 1 to n.
Mode
- The mode is the value of the observation which occurs most frequently, i.e., an observation with the maximum frequency is called the mode of the data.
- Note: In a given dataset, the value around which there is the greatest concentration is called the mode of the data.
Median
- After arranging the given data in an ascending or a descending order of magnitude, the value of the middle-most observation is called the median of the data.
- Note: For ‘n’ observations (taken in order),
(i) if n is odd, the median = value ofobservation.
(ii) if n is even, the median = mean ofobservations.
|
40 videos|471 docs|57 tests
|
FAQs on NCERT Solutions for Class 9 Maths - Statistics (Exercise 12.1)
| 1. What is the importance of statistics in everyday life? |  |
| 2. How can I calculate the mean, median, and mode from a data set? |  |
| 3. What are the different types of data represented in statistics? |  |
| 4. What is the difference between descriptive and inferential statistics? |  |
| 5. How can I interpret the results of a statistical analysis? |  |

















