Class 10 Maths Chapter 3 Question Answers - Pair of Linear Equations in Two Variables
Q1: For what value of p, the pair of linear equations px = 2y; 2x - y + 5 = 0 has unique solution?
Sol: We have: px = 2y
⇒ p - 2y = 0
2x = y + 5
⇒ 2x - y = - 5
Here, a1 = p, b1 = - 2,
c1 = 0
a2 = 2, b2 = - 1,
c2 = - 5
For a unique solution,
a1a2 ≠ b1b2
Substitute the values:
p2 ≠ -2-1
p2 ≠ 2
p ≠ 4
Q2: In a cyclic quadrilateral PQRS, ∠P = (2x + 4)°, ∠Q = (y + 3)°, ∠R = (2y + 10)° and ∠S = (4x - 5)°. Find its four angles.
Sol: In a cyclic quadrilateral, the sum of opposite angles is 180°.
From ∠P + ∠R = 180°:
(2x + 4) + (2y + 10) = 180 → 2x + 2y = 166 (Equation 1)
From ∠Q + ∠S = 180°:
(y + 3) + (4x - 5) = 180 → 4x + y = 182 (Equation 2)
Solving the equations:
From Equation 1: y = 83 - x
Substitute into Equation 2:
4x + (83 - x) = 182 → 3x + 83 = 182 → x = 33
Find y:
y = 83 - 33 = 50
Calculate the angles:
- ∠P = 2x + 4 = 70°
- ∠Q = y + 3 = 53°
- ∠R = 2y + 10 = 110°
- ∠S = 4x - 5 = 127°
Therefore, ∠P = 70°, ∠Q = 53°, ∠R = 110°, ∠S = 127°
Q3: Solve:
23x + 35y = 209
35x + 23y = 197
Sol: We have:
23x + 35y = 209 ...(1)
35x + 23y = 197 ...(2)
58x + 58y = 406 [Adding (1) and (2)]
⇒ x + y = 7 ...(3) [Dividing by whole equation by 58]
Subtracting (1) from (2),
We get,
12x - 12y = - 12
⇒ x - y = 1 ...(4) [Dividing whole equation by 12]
Adding (3) and (4),We get,
x + y + x - y = 7 + 1
⇒ 2x = 8 ⇒ x = 4
Putting the value of x = 4 in (3)
We get,
x + y = 7 ⇒ 4 + y = 7
⇒ y = 3
So, x = 4 and y = 3.
Q4: Solve:
3x + 5y = 70 ...(1)
7x - 3y = 60 ...(2)
Sol: To solve the equations:
3x + 5y = 70
7x - 3y = 60
Step 1: Eliminate one variable
Multiply Equation (1) by 3 and Equation (2) by 5:
(9x + 15y = 210)
(35x - 15y = 300)
Add the two equations:
(44x = 510)
x = 51044 = 25522
Step 2: Substitute x into Equation (1)
Substitute x = 25522 into 3x + 5y = 70:
3 x 25522 + 5y = 70
76522 + 5y = 70
5y = 70 - 76522
5y = 154022 - 76522
5y = 77522
y = 775110 = 15522
Therefore, x = 25522, y = 15522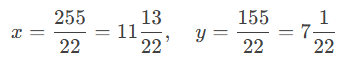
Q5: Without drawing the graphs, state whether the following pair of linear equations will represent intersecting lines, coinciding lines or parallel lines:
6x - 3y + 10 = 0
2x - y + 9 = 0
Sol: Here, the given set of equations is:
6x - 3y + 10 = 0 ...(1)
2x - y + 9 = 0 ...(2)
From (1) and (2), we have:
a1 = 6, b1 = - 3, c1 = 10
a2 = 2, b2 = - 1, c2 = 9
Now , a1a2 = 62 = 3
∴ We have: a1a2 = b1b2 ≠ c1c2
This condition represents parallel lines. Hence, the given pair represents parallel lines.
Q6: Check graphically whether the pair of equations
3x - 2y + 2 = 0
32 x - y + 3 = 0
is consistent. Also find the co-ordinates of the points where the graphs of the equations meet the y-axis.
Sol: 3x − 2y + 2 = 0 ⇒ y = 3x − 22 ... (1)
| x | 0 | 2 | −2 |
|---|---|---|---|
| y | 1 | 4 | −2 |
| (x, y) | (0, 1) | (2, 4) | (−2, −2) |
Also, 0 = y = 32 x − y + 3 = ... (2)
0 ⇒ y = 32 x + 3
| x | 0 | 2 | −2 |
|---|---|---|---|
| y | 3 | 6 | 0 |
| (x, y) | (0, 3) | (2, 6) | (−2, 0) |
Plotting the points (0, 1), (2, 4), (- 2, - 2) and (0, 3), (2, 6), (–2, 0) we get two straight lines l1 and l2 which are parallel.
∴ The given equations are inconsistent.
From the graph, we observe that line l1 meets the y-axis at (0, 1) and line l2 meets the y-axis at (0, 3).
Q7: A fraction becomes 1/3 if 2 is added to both numerator and denominator. If 3 is added to both numerator and denominator, it becomes 2/5. Find the fraction.
Sol: Let the fraction be: xy
From the first condition: x + 2y + 2 = 13
Cross-multiplying:
3(x + 2) = y + 2
Simplify:
3x - y = -4 (1)
From the second condition: x + 3y + 3 = 25
Cross-multiplying:
5(x + 3) = 2(y + 3)
Simplify:
5x - 2y = -9 (2)
From Equation (1):
y = 3x + 4 (3)
Substitute y = 3x + 4 into Equation (2):
5x - 2(3x + 4) = -9
Simplify:
-x = -1 , x = 1
Substitute x = 1 into Equation (3):
y = 3(1) + 4 = 7
Thus, the fraction is: 17
Q8: Check graphically whether the pair of equations
3x + 5y = 15
x - y = 5
is consistent. Also, find the coordinates of the points where the graphs of equations meet the y-axis.
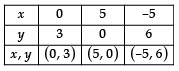
Sol: We have
3x + 5y = 15
⇒ y = 15 - 3x5
∴ 
And from x - y = 5
⇒ y = x - 5
Plotting the above two sets of points we get two straight lines l1 and l2 which intersect at the point (5, 0).
Thus, the given system is consistent.
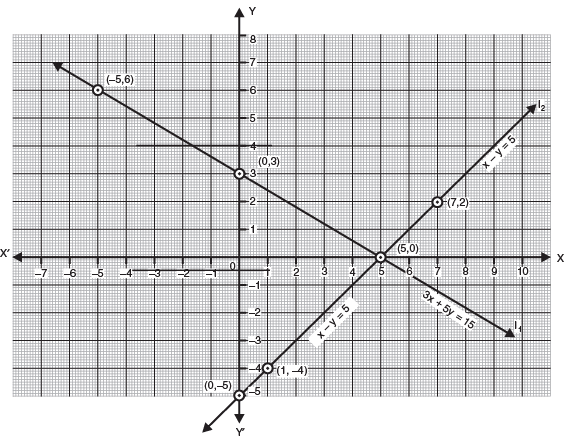
Obviously, line l1 meets the y-axis at (0, 3) and line l2 meets the y-axis at (0, - 5).
Q9: Places A and B are 160 km apart on the highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 8 hours, but if they travel towards each other, they meet in 2 hours. What are the speeds of the two cars?
Sol: Let the car-I and car-II start from A and B at x km/hr and y km/hr respectively.
Case-I: [Cars are moving in the same direction]
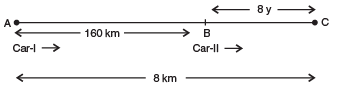
Let the two cars meet at C after 8 hours.
Distance covered:
by car-I = AC = 8x km
by car-II = BC = 8y km
∴ AB = AC - BC
⇒ 160 = 8x - 8y
⇒ x - y = 20 ...(1)
Case-II: [Cars are moving in opposite directions]

Let, after 2 hours, the cars meet at D.
∴ Distance cover after 2 hours,
by car-I = AD = 2x km
by car-II = BD = 2y km
⇒ AB = AD + BD
⇒ 160 = 2x + 2y
⇒ 80 = x + y
⇒ x + y = 80 ...(2)
Adding (1) and (2), we get
x + y = 80
x - y = 20
2x = 100
⇒ x = 100/2 = 50
⇒ Substituting x = 50 in (1), we get
x - y = 20 ⇒ 50 - y = 20
⇒ y = 50 - 20 = 30
⇒ Speed of car-I = 50 km/hr
Speed of car-II = 30 km/hr.
Q10: The sum of two numbers is 8. Determine the numbers if the sum of their reciprocals is 8/15.
Sol: Let the two numbers be x and y.
According to the conditions:
x + y = 8 ...(1)
= 1x + 1y = 815 ... (2)
From (1), x = (8 - y)
Substituting x = (8 - y) in (2),
1(8 - y) + 1y = 815
⇒ y + 8 - y(8 - y)y = 815
⇒ 8 × 15 = 8 × y (8 - y)
⇒ 64y - 8y2 - 120 = 0
⇒- y2 + 8y - 15 = 0
⇒ y2 - 8y + 15 = 0
⇒ y2 - 5y - 3y + 15 = 0
⇒ y (y - 5) - 3 (y - 5) = 0
⇒ (y - 5) (y - 3) = 0
⇒ If y - 5 = 0 then y = 5
or if y - 3 = 0, then y = 3
Since x = 8 - y
⇒ when y = 5,
then x = 8 - 5 = 3
when y = 3, then
x = 8 - 3 = 5
⇒ The required numbers are (3, 5) or (5, 3).
Q11: Solve the following pair of equations:
5x - 1 + 1y - 2 = 2
6x - 1 - 3y - 2 = 1
Sol: Let p = 1x - 1 and q = 1y - 2
⇒The given system of equations becomes:
5p + q = 2 ...(1)
6p - 3q = 1 ...(2)
Multiplying (1) by 3 and adding to (2),
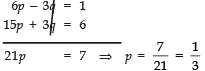
⇒21p = 7
⇒p = 721 = 13
⇒ p = 13
and 5p + q = 2
⇒ 5(13) + q = 2
⇒ 53 + q = 2
⇒ q = 2 - 53 = 13
⇒ q = 13
Since, p = 1x - 1
therefore 1x - 1 = 13 ⇒ x - 1 = 3
⇒ x = 4
Also, q = 1y - 2
⇒ y - 2 = 3 ⇒ y = 5
Q12: Solve the following pair of equations:
10x + y + 2x − y = 4
15x + y − 5x − y = −2
Sol: Let 1x + y = p and 1x − y = q
⇒ The given pair of equation is expressed as
10p + 2q = 4 ⇒ 5p + q = 2 ...(1)
15p - 5q = - 2 ...(2)
Multiplying (1) by 5 and adding to (2)
From (1), 5 ( 51 ) + q = 2
⇒ 1 + q = 2 ⇒ q = 2 − 1 = 1
Since, p = 1x + y
⇒ 1x + y = 15
⇒ x + y = 5 ... (3)
And q = 1x − y ⇒ 1x − y = 1
⇒ x − y = 1 ...(4)
Adding (3) and (4),
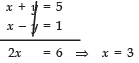
From (3), 3 + y = 5 ⇒ y = 2
Thus, x = 3 and y = 2.
Q13: Solve for x and y:
37x + 43y = 123
43x + 37y = 117
Sol: We have:
37x + 43y = 123 ...(1)
43x + 37y = 117 ...(2)
Adding (1) and (2)
43x + 37y = 117
Dividing both sides by 80, we get
x + y = 3 ...(3)
Subtracting (2) from (1),
- 6x + 6y = 6 ⇒ - x + y = 1 ...(4)
Adding:
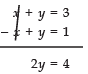
⇒ y = 4/2 = 2
Putting y = 2 in x + y = 3, we get
x + 2 = 3 ⇒ x = 3 - 2 = 1
Thus, x = 1 and y = 2.
Q14: Represent the following pair of equations graphically and write the co-ordinates of points where the lines intersect y-axis:
x + 3y = 6, 2x - 3y = 12
Sol: We have:
x + 3y = 6
| x | 0 | 3 | 6 |
| y | 2 | 1 | 0 |
| (x, y) | (0, 2) | (3, 1) | (6, 0) |
And 2x - 3y = 12:
| x | 6 | 3 | 0 |
| y | 0 | -2 | -4 |
| (x, y) | (6, 0) | (3, -2) | (0, -4) |
Plotting the above points, we get two straight lines l1 and l2 such that they intersect at (6, 0) as shown below:
Obviously,
The line l1 meets the y-axis at (0, 2).
The line l2 meets the y-axis at (0, - 4).
Q15: Draw the graph of the pair of linear equations x – y + 2 = 0 and 4x – y – 4 = 0. Calculate the area of triangle formed by the lines so drawn and the x-axis.
Sol: To draw the graph of the given pair of equations, we have the table of ordered pairs
x - y + 2 = 0
| x | 0 | -2 |
| y | 2 | 0 |
| (x, y) | (0, 2) | (-2, 0) |
4x - y - 4 = 0
| x | 0 | 1 |
| y | -4 | 0 |
| (x, y) | (0, -4) | (1, 0) |
Plot the points A(0, 2), B(–2, 0); C(0, –4) and D(1, 0) on the graph paper and join the points to form the lines AB and CD :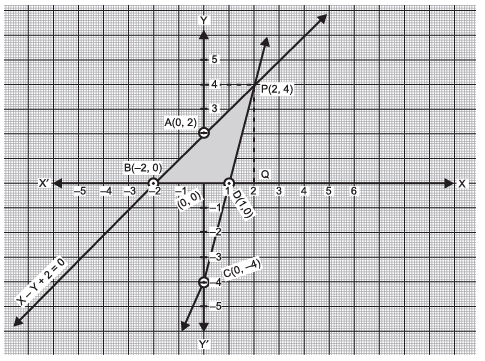
From the graph, we find that the points P(2, 4) is common to both the lines AB and CD.
These lines meet the x-axis at B(–2, 0) and D(1, 0).
Thus, the triangle BDP is formed by the lines and the x-axis.
The vertices of this Δ are
B(–2, 0), D(1, 0) and P(2, 4)
Now, the base of ΔBDP = BD
= (BO + OD)
= (2 + 1) units
= 3 units
Altitude of the ΔBDP = PQ
= 4 units
∴ Area of ΔBDP = 12 × base × altitude
= 12 × BD × PQ
= 12 × 3 × 4 units
= 6 sq. units
Q16: It can take 12 hours to fill a swimming pool using two pipes. If the pipe of larger diameter is used for 4 hours and the pipe of smaller diameter for 9 hours, only half the pool can be filled. How long would it take for each pipe to fill the pool separately?
Sol: Let the time taken by the pipe of larger diameter to fill the pool separately = x hours.
The time taken by the pipe of smaller diameter to fill the pool separately = y hours.
∴ Part of the pool fill by a pipe of larger diameter in 1 hour = 1/x.
Part of fool filled by the pipe of larger diameter in 4 hours = 4/x.
Similarly, Part of the pool filled by the pipe of smaller diameter in 9 hours = 9/y.
∴ We have 4x + 9y = 12 ...(1)
Since the pool is filled by both the pipes together in 12 hours.
∴ 12x + 12y = 1 ...(2)
To solve (1) and (2), multiplying (1) by 3 and subtracting (2) from it, we have
3[ 4x + 9y] − [ 12x + 12y] = 1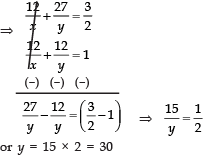
Substituting, y = 30 in (2), we have
12x + 1230 = 1
⇒ 12x = 1 − 25 = 1830 = 120
∴ x = 20
⇒ Required time taken by pipe of larger diameter = 20 hours
⇒ Required time taken by pipe of smaller diameter = 30 hours
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Maths Chapter 3 Question Answers - Pair of Linear Equations in Two Variables
| 1. What are the methods to solve a pair of linear equations in two variables? |  |
| 2. How can we determine if a pair of linear equations has no solution, one solution, or infinitely many solutions? |  |
| 3. Can you explain how to solve a pair of linear equations using the elimination method with an example? |  |
| 4. What is the significance of the graphical representation of linear equations in two variables? |  |
| 5. How do you convert a pair of linear equations into a matrix form? |  |

















