NCERT Solutions for Class 9 Maths Chapter 15 - Exercise 15.1 Probability
Q.1. In a cricket match, a batswoman hits a boundary 6 times out of 30 balls she plays. Find the probability that she did not hit a boundary.
Sol.
According to the question,
Total number of balls = 30
Numbers of boundary = 6
Number of time batswoman didn’t hit boundary = 30 – 6 = 24
Probability she did not hit a boundary = 24/30 = 4/5
Q.2. 1500 families with 2 children were selected randomly, and the following data were recorded:
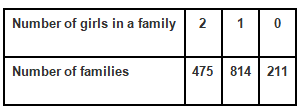
Compute the probability of a family, chosen at random, having
(i) 2 girls
(ii) 1 girl
(iii) No girl
Also, check whether the sum of these probabilities is 1.
Sol.
Total numbers of families = 1500
(i) Numbers of families having 2 girls = 475
Probability = Numbers of families having 2 girls/Total numbers of families
= 475/1500 = 19/60
(ii) Numbers of families having 1 girls = 814
Probability = Numbers of families having 1 girls/Total numbers of families
= 814/1500 = 407/750
(iii) Numbers of families having 2 girls = 211
Probability = Numbers of families having 0 girls/Total numbers of families = 211/1500
Sum of the probability = (19/60)+(407/750)+(211/1500)
= (475+814+211)/1500
= 1500/1500 = 1
Yes, the sum of these probabilities is 1.
Q.3. Refer to Example 5, Section 14.4, Chapter 14. Find the probability that a student of the class was born in August.
Sol. 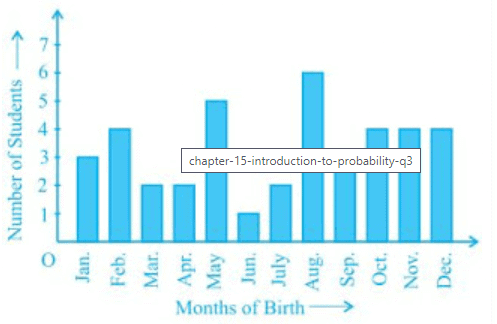
Total numbers of students in the class = 40
Numbers of students born in August = 6
The probability that a student of the class was born in August, = 6/40 = 3/20
Q.4. Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes:
If the three coins are simultaneously tossed again, compute the probability of 2 heads coming up.
Sol.
Number of times 2 heads come up = 72
Total number of times the coins were tossed = 200
∴, the probability of 2 heads coming up = 72/200 = 9/25
Q.5. An organisation selected 2400 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a family. The information gathered is listed in the table below:
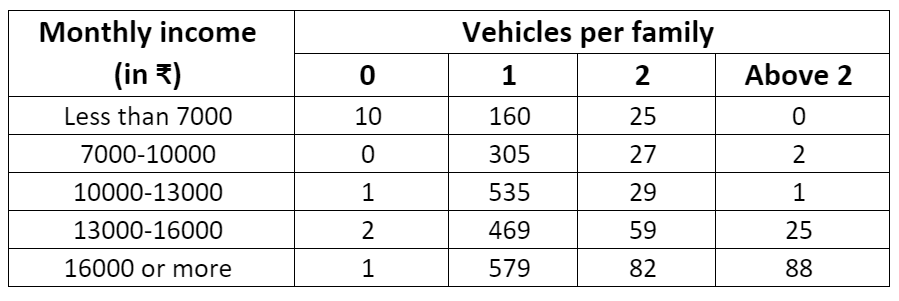
(i) earning Rs. 10000–13000 per month and owning exactly 2 vehicles.
(ii) earning Rs. 16000 or more per month and owning exactly 1 vehicle.
(iii) earning less than Rs. 7000 per month and does not own any vehicle.
(iv) earning Rs. 13000–16000 per month and owning more than 2 vehicles.
(v) owning not more than 1 vehicle.
Sol.
Total number of families = 2400
(i) Numbers of families earning ₹10000 –13000 per month and owning exactly 2 vehicles = 29
∴, the probability that the family chosen is earning ₹10000 – 13000 per month and owning exactly 2 vehicles = 29/2400
(ii) Number of families earning ₹16000 or more per month and owning exactly 1 vehicle = 579
∴ the probability that the family chosen is earning₹16000 or more per month and owning exactly 1 vehicle = 579/2400
(iii) Number of families earning less than ₹7000 per month and does not own any vehicle = 10
∴ the probability that the family chosen is earning less than ₹7000 per month and does not own any vehicle = 10/2400 = 1/240
(iv) Number of families earning ₹13000-16000 per month and owning more than 2 vehicles = 25
∴ the probability that the family chosen is earning ₹13000 – 16000 per month and owning more than 2 vehicles = 25/2400 = 1/96
(v) Number of families owning not more than 1 vehicle
= 10+160+0+305+1+535+2+469+1+579 = 2062
∴ the probability that the family chosen owns not more than 1 vehicle = 2062/2400 = 1031/1200
Q.6. Refer to Table 14.7, Chapter 14.
(i) Find the probability that a student obtained less than 20% in Mathematics test.
(ii) Find the probability that a student obtained 60 marks or above.
Sol. From the table 14.7, we have: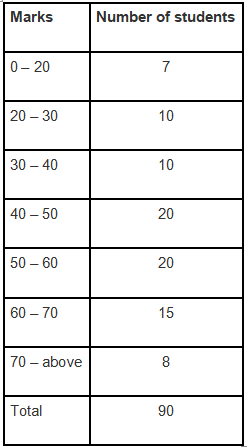
Total number of students = 90
(i) Number of students who obtained less than 20% in the mathematics test = 7
∴ the probability that a student obtained less than 20% in the mathematics test = 7/90
(ii) Number of students who obtained marks 60 or above = 15+8 = 23
∴ the probability that a student obtained marks 60 or above = 23/90
Q.7. To know the opinion of the students about the subject statistics, a survey of 200 students was conducted. The data is recorded in the following table.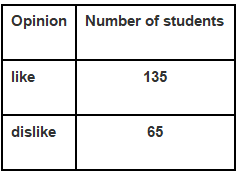
Find the probability that a student chosen at random
(i) likes statistics
(ii) does not like it.
Sol.
Total number of students = 135+65 = 200
(i) Number of students who like statistics = 135,
the probability that a student likes statistics = 135/200 = 27/40
(ii) Number of students who do not like statistics = 65
∴, the probability that a student does not like statistics = 65/200 = 13/40
Q.8. What is the empirical probability that an engineer lives:
(i) less than 7 km from her place of work?
(ii) More than or equal to 7 km from her place of work?
(iii) Within (1/2) km from her place of work?
Sol.
The distance (in km) of 40 engineers from their residence to their place of work were found as follows:
Total numbers of engineers = 40
(i) Number of engineers living less than 7 km from their place of work = 9,
the probability that an engineer lives less than 7 km from her place of work = 9/40
(ii) Number of engineers living more than or equal to 7 km from their place of work = 40-9 = 31,
probability that an engineer lives more than or equal to 7 km from her place of work = 31/40
(iii) Number of engineers living within ½ km from their place of work = 0
∴, the probability that an engineer lives within ½ km from her place of work = 0/40 = 0
Q.9. Activity: Note the frequency of two-wheelers, three-wheelers and four-wheelers going past during a time interval, in front of your school gate. Find the probability that any one vehicle out of the total vehicles you have observed is a two-wheeler.
Sol.
The question is an activity to be performed by the students.
Hence, perform the activity by yourself and note down your inference.
Q.10. Activity: Ask all the students in your class to write a 3-digit number. Choose any student from the room at random. What is the probability that the number written by her/him is divisible by 3?
Sol. A classroom activity for students.
Remember: A number is divisible by 3 if the sum of its digits is divisible by 3.
Examples: (i) Number 45678 is divisible by 3 because 4 + 5 + 6 + 7 + 8 = 30 is divisible by 3.
(ii) Number 10786 is not divisible by 3 because 1 + 0 + 7 + 8 + 6 = 22 is not divisible by 3.
Q.11. Eleven bags of wheat flour, each marked 5 kg, actually contained the following weights of flour (in kg):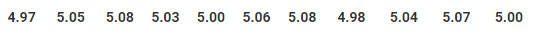
Find the probability that any of these bags chosen at random contains more than 5 kg of flour.
Sol. Total number of bags = 11
∵ Number of bags having more than 5 kg of flour = 7
∴ the probability that any of the bags chosen at random contains more than 5 kg of flour = (7/11)
Q.12. In this question, you were asked to prepare a frequency distribution table, regarding the concentration of sulphur dioxide in the air in parts per million of a certain city for 30 days. Using this table, find the probability of the concentration of sulphur dioxide in the interval 0.12–0.16 on any of these days.
The data obtained for 30 days is as follows: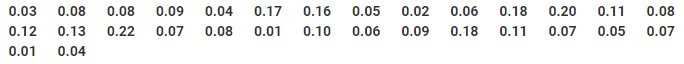
Sol.
Total number of days in which the data was recorded = 30 days
Numbers of days in which sulphur dioxide was present in between the interval 0.12-0.16 = 2
∴ the probability of the concentration of sulphur dioxide in the interval 0.12-0.16 on any of these days = 2/30 = 1/15
Q.13. In this question, you were asked to prepare a frequency distribution table regarding the blood groups of 30 students of a class. Use this table to determine the probability that a student of this class, selected at random, has blood group AB.
The blood groups of 30 students of Class VIII are recorded as follows:
A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O, A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O.
Sol.
Total numbers of students = 30
Number of students having blood group AB = 3
∴, the probability that a student of this class, selected at random, has blood group AB = 3/30 = 1/10
|
276 docs|155 tests
|
FAQs on NCERT Solutions for Class 9 Maths Chapter 15 - Exercise 15.1 Probability
| 1. What is probability and how is it calculated? |  |
| 2. How is probability used in real life? |  |
| 3. What are the different types of probability? |  |
| 4. What is conditional probability? |  |
| 5. How does probability relate to statistics? |  |

















