Class 10 Maths Chapter 11 Question Answers - Area Related to Circles
Q1: If the difference between the circumference and the radius of a circle is 37 cm, then using π = 22/7, calculate the circumference (in cm) of the circle.
Sol: 2πr – r = 37 ⇒ r(2π – 1) = 37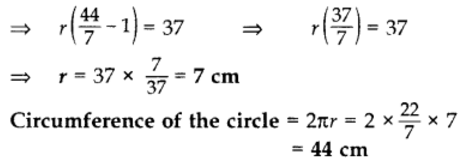
Q2: If he is taken as 22/7, calculate the distance (in metres) covered by a wheel of diameter 35 cm, in one revolution.
Sol: Radius (r) = 35/2
Required distance = Perimeter = 2πr
= 2 × 22/7 × 35/7 cm = 110 cm or 1.1 m
Q3: In the Figure, PQ and AB are respectively the arcs of two concentric circles of a radii 7 cm and 3.5 cm and centre O. If ∠POQ = 30°, then find the area of the shaded region. [Use π = 22/7] Sol: Area of sector with radius 7 cm
Sol: Area of sector with radius 7 cm
Q4: Find the area of the major segment APB, in the figure of a circle of radius 35 cm and ∠AOB = 90°. (Use π = 22/7) Sol: Here θ = 90°, p = OA = OB = 35 cm
Sol: Here θ = 90°, p = OA = OB = 35 cm
Area of minor segment = ar(minor sector) – ar(∆AOB)
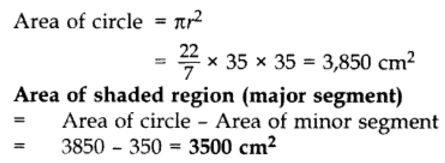
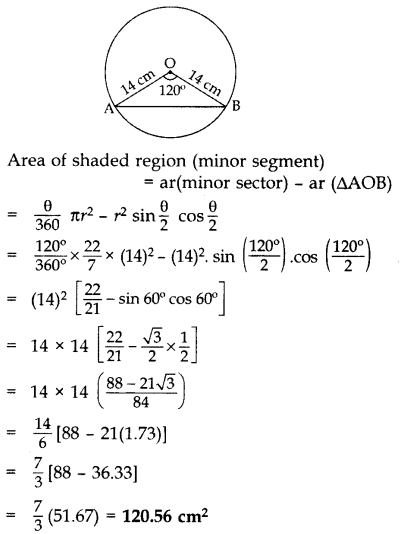
Q5: A chord of a circle of radius 14 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle. (Use π = 22/7 and √3 = 1.73)
Sol: Here θ = 120°, r = 14 cm
Q6: In Figure, O is the centre of a circle such that diameter AB = 13 cm and AC = 12 cm. BC is joined. Find the area of the shaded region. (Take π = 3.14)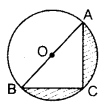 Sol: ∠ACB = 90° …[Angle in a semi-circle
Sol: ∠ACB = 90° …[Angle in a semi-circle
∴ AC2 + BC2 = AB2 …[Pythagoras’ theorem
(12)2 + BC2 = (13)2
144 + BC2 = 169
BC2 = 169 – 144 = 25
BC = + 5 cm
Q7: In Figure, ABC is a right-angled triangle right angled at A. Semicircles are drawn on AB, AC and BC as diametres. Find the area of the shaded region.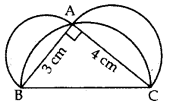 Sol: In rt. ∆BAC,
Sol: In rt. ∆BAC,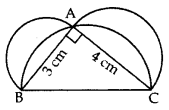
∴ BC2 = AB2 + AC2 …[Pythagoras’ theorem
= (3)2 + (4)
= 9 + 16 = 25 cm2
∴ BC = +5 cm … [Side of ∆ can’t be -ve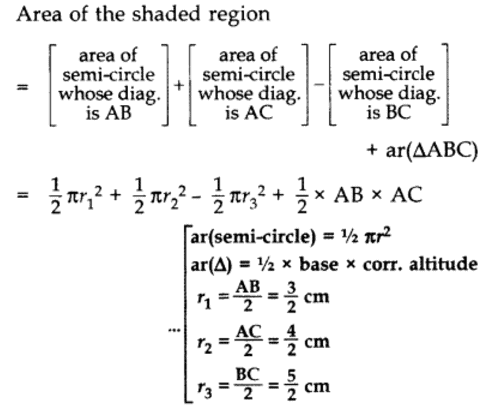
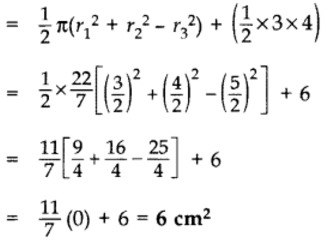
Q8: In the given figure, OAPB is a sector of a circle of radius 3.5 cm with the centre at O and ∠AOB = 120°. Find the length of OAPBO.

Sol: Here, the major sector angle is given by θ = 360° − 120° = 240°

∴ Circumference of the sector APB
∴ Perimeter of OAPBO = [Circumference of sector AOB] + OA + OB]


Q9: Find the area of a square inscribed in a circle of radius 10 cm.
Sol: Let ABCD be the square such that

AB = BC = 10 cm
∴ AC2 = AB2 + BC2
AB2 + BC2 = (10 × 2)
⇒ x2 + x2 = (20)2
[Let AB = BC = x]
⇒ 2x2 = 400
⇒ 
∴ Area of the square = 200 cm2.
Q10: In the given figure, O is the centre of a circular arc and AOB is a straight line. Find the perimeter of the shaded region.

Sol. O is the centre of the circle.
∴ AB is its diameter.
In right Δ ABC,
AC2 + BC2 = AB2
⇒ 122 + 162 = AB2
⇒ 144 + 256 = AB2 ⇒ AB2 = 400
⇒ 
∴ Circumference of semi-circle ACB
∴ Perimeter of the shaded region = 22/7 cm + 12 cm + 16 cm
= 31.43 cm + 12cm + 16cm
= 59.43 cm
|
126 videos|457 docs|75 tests
|
FAQs on Class 10 Maths Chapter 11 Question Answers - Area Related to Circles
| 1. What is the formula for the area of a circle? |  |
| 2. How do you calculate the circumference of a circle? |  |
| 3. What is the relationship between the radius and diameter of a circle? |  |
| 4. How can you find the area of a circle if you only know the diameter? |  |
| 5. What units are used when measuring the area of a circle? |  |

|
Explore Courses for Class 10 exam
|

|


















