Class 10 Maths Chapter 5 Question Answers - Arithmetic Progressions - 1
Note: For an A.P. with the 1st term and common difference ‘a’ and ‘d’ respectively, we have :
(a) nth term from the end = (m – n +1)th term from the beginning, where m is the number of terms in the A.P.
⇒ nth term from the end = (a) + (m – n)d
(b) If ‘l’ is the last term of the A.P., then
nth term from the end is the nth term of an A.P. whose first term is ‘l’ and the common difference is ‘–d’
⇒ nth term from the end = l + (n – 1) (–d)
 Arithmetic Progression
Arithmetic Progression
Q1. If 9th term of an A.P. is zero, prove that its 29th term is double of its 19th term
Sol. Let ‘a’ be the first term and ‘d’ be the common difference.
Now, Using Tn = a + (n - 1) d, we have
T9 = a + 8d ⇒ a + 8d = 0 ...(1) [∵ T9 = 0 Given]
T19 = a + 18d = (a + 8d) + 10d = (0) + 10d = 10d ...(2)
[∵ a + 8d = 0]
T29 = a + 28d
= (a + 8d) + 20d
= 0 + 20d = 20d [∵ a + 8d = 0]
= 2 × (10d) = 2 (T19) [∵ T19 = 10d]
⇒ T29 = 2 (T19)
Thus, the 29th term of the A.P. is double of its 19th term.
Q2. If Tn = 3 + 4n then find the A.P. and hence find the sum of its first 15 terms.
Sol. Let the first term be ‘a’ and the common difference be ‘d’.
∵ Tn = a + (n - 1) d
∴ T1 = a + (1 - 1) d = a + 0 × d = a
T2 = a + (2 - 1) d = a + d
But it is given that
Tn = 3 + 4n
∴ T1 = 3 + 4 (1) = 7
⇒ First term, a = 7
Also, T2 = a + d = 3 + 4 (2) = 11
∴d = T2 - T1 = 11 - 7 = 4
Now, using Sn = n/2 [2a + (n - 1) d],
we get
S15 = 15/2 [2 (7) + (15 - 1) × 4]
= 152 [14 + 14 × 4]
= 152 [70]
= 15 × 35 = 525
Thus, the sum of the first 15 terms = 525.
Q3. Which term of the A.P.:
3, 15, 27, 39, ..... will be 120 more than its 53rd term?
Sol. The given A.P. is:
3, 15, 27, 39, .....
∴ a = 3
d = 15 - 3 = 12
∴ Using, Tn = a + (n - 1) d, we have:
T53 = 3 + (53 - 1) × 12
= 3 + (52 × 12)
= 3 + 624 = 627
Now, T53 + 120 = 627 + 120 = 747.
Let the required term be Tn
∴ Tn = 747
or a + (n - 1) d = 747
∴ 3 + (n - 1) × 12 = 747
⇒ (n - 1) × 12 = 747 - 3 = 744
⇒ n - 1 = 744/12 = 62
⇒ n = 62 + 1 = 63
Thus, the 63rd term of the given A.P. is 120 more than its 53rd term.
Q4. Find the 31st term of an A.P. whose 10th term is 31 and the 15th term is 66.
Sol. Let the first term is ‘a’ and the common difference is ‘d’.
Using Tn = a + (n - 1) d, we have:
T10 = a + 9d
⇒ 31 = a + 9d ...(1)
Also T15 = a + 14d
⇒ 66 = a + 14d ...(2)
Subtracting (1) from (2), we have:
a + 14d - a - 9d = 66 - 31
⇒ 5d = 35
⇒ d = 35/5 = 7
∴ From (1), a + 9d = 31
⇒ a + 9 (7) = 31
⇒ a + 63 = 31
⇒ a = 31 - 63
⇒ a = - 32
Now, T31 = a + 30d
= - 32 + 30 (7)
= - 32 + 210 = 178
Thus, the 31st term of the given A.P. is 178.
Q5. If the 8th term of an A.P. is 37 and the 15th term is 15 more than the 12th term, find the A.P. Hence find the sum of the first 15 terms of the A.P.
Sol. Let the 1st term = a
And the common difference = d
∴ Using Tn = a + (n - 1) d
∴ T8 = a + 7d
⇒ 37 = a + 7d ...(1)
Also T15 = a + 14d
And T12 = a + 11d
According to the question,
T15 = T12 + 15
⇒ a + 14d = a + 11d + 15
⇒ a - a + 14d - 11d = 15
⇒ 3d = 15 ⇒ d = 15/3 = 5
From (1), we have:
a + 7 (5) = 37
⇒ a + 35 = 37
⇒ a = 37 - 35 = 2
Since an A.P. is given by :
a, a + d, a + 2d, a + 3d, ....
∴ The required A.P. is given by 2, 2 + 5, 2 + 2(5),... 2, 7, 12, ...
Now, using Sn = n/2 [2a + (n - 1) d]
∴ S15 = n/2 [2 (2) + 14 × 5]
= 15/2 [4 + 70]
= 152 × 74 = 15 × 37
= 555
Q6. The 5th and 15th terms of an A.P. are 13 and - 17 respectively. Find the sum of first 21 terms of the A.P.
Sol. Let ‘a’ be the first term and ‘d’ be the common difference.
∴ Using Tn = a + (n - 1) d, we have:
T15 = a + 14d = - 17 ...(1)
T5 = a + 4d = 13 ...(2)
Subtracting (2) from (1), we have:
(T15 - T5) = - 17 - 13 = - 30
⇒ a + 14d - a - 4d = - 30
⇒ 10d = - 30 ⇒ d = - 3
Substituting d = - 3 in (2), we get
a + 4d = 13
⇒ a + 4 (- 3) = 13
⇒ a + (- 12) = 13
⇒ a = 13 + 12 = 25
Now using Sn = n/2 [2a + (n - 1) d] we have:
S21 = 21/2 [2 (25) + (21 - 1) × (- 3)]
= 21/2[50 + (- 60)]
= 212 × -10
= 21 × (-5) = -105
Thus, the sum of the first fifteen terms = - 105.
Q7. The 1st and the last term of an A.P. are 17 and 350 respectively. If the common difference is 9 how many terms are there in the A.P.? What is their sum?
Sol. Here, first term, a = 17
Last term Tn = 350 = l
∵ Common difference (d) = 9.
∴ Using Tn = a + (n - 1) d, we have:
350 = 17 + (n - 1) × 9
⇒ n - 1 = 350 - 179
= 3339 = 37
⇒ n = 37 + 1 = 38
Thus, there are 38 terms.
Now, using, Sn = n/2 [a + l], we have
S38 = 38/2 [17 + 350]
= 19 [367] = 6973
Thus, the required sum of 38 terms
= 6973.
Q8. If the sum of the first 7 terms of an A.P. is 49 and that of the first 17 terms is 289, find the sum of n terms.
Sol. Let the first term = a and the common difference = d.
∴ Using Sn = n/2 [2a + (n - 1) d]
∴ S7 = 7/2 [2a + 6d] = 49
⇒ 72 × 2 [a + 3d] = 49
⇒ 7 [a + 3d] = 49
⇒ a + 3d = 49/7 = 7
i.e., a + 3d = 7 ...(1)
Also S17 = 17/2 [2a + 16d] = 289
⇒ 172 × 2 [a + 8d] = 289
⇒ 17 [a + 8d] = 289
⇒ a + 8d = 289/17 = 17
⇒ a + 8d = 17 ...(2)
Subtracting (2) from (1), we have:
a + 8d - a - 3d = 17 - 7
⇒ 5d = 10 ⇒ d = 2
From (1), we have
a + 3 (2) = 7
⇒ a + 6 = 7 ⇒ a = 7 - 6 = 1
Now, Sn = n/2 [2a + (n - 1) d]
= n2 [2 × 1 + (n - 1) × 2]
= n2 [2 + 2n - 2]
= n2 [2n]
Thus, the sum of n terms is n2.
Q9. The first and last term of an A.P. is 4 and 81 respectively. If the common difference is 7, how many terms are there in the A.P. and what is their sum?
Sol. Here, first term = 4 ⇒ a = 4 and d = 7.
Last term, l = 81 ⇒ Tn = 81
∵ Tn = a + (n - 1) d
∴ 81 = 4 + (n - 1) × 7
⇒ 81 - 4 = (n - 1) × 7
⇒ 77 = (n - 1) × 7
⇒ n = 777 + 1 = 11 + 1 = 12
⇒ There are 12 terms.
Now, using
Sn = n/2 (a + l)
⇒ S12 = 12/2 (4 + 81)
⇒ S12 = 6 × 85 = 510
∴ The sum of 12 terms of the A.P. is 510.
Q10. The angles of a quadrilateral are in A.P. whose common difference is 15°. Find the angles.
Sol. Let one of the angles = a
∵ The angles are in an A.P.
∴ The angles are:
a°, (a + d)°, (a + 2d)° and (a + 3d)°
∵ d = 15 [Given]
∴ The angles are:
a, (a + 15), [a + 2 (15)] and [a + 3 (15)]
i.e., a, (a + 15), (a + 30) and (a + 45).
∵ The sum of the angles of a quadrilateral is 360°.
∴ a + (a + 15) + (a + 30) + (a + 45) = 360°
⇒ 4a + 90° = 360°
⇒ 4a = 360° - 90° = 270°
⇒ a = 270°4 = 67 12 °
∴ The four angles are:
67 12 °, (67 12 + 15)°, (67 12 + 30)°, and (67 12 + 45)°
or 67 12 °, 82 12 °, 97 12 °, and 112 12 °
Q11. The angles of a triangle are in AP. The greatest angle is twice the least. Find all the angles of the triangle.
Sol. Let a, b, c are the angles of the triangle, such that
c = 2a ...(1)
Since a, b, c are in A.P.
Then b = a + c2 ...(2)
From (1) and (2), we get
a + 2a2, 2a, a are the three angles of the triangle.
∴ a + a + 2a2 + 2a = 180°
⇒2a + a + 2a + 4a = 360°
⇒ 9a = 360°
⇒ a = 360°/9 = 40°
∴ The smallest angle = 40°
The greatest angle = 2a = 2 × 40° = 80° The third angle
= a + c2 = 40 + 802 = 60°
Thus the angles of the triangle are 40°, 60°, 80°.
Q12. Find the middle term of the A.P. 10, 7, 4, ....., - 62.
Sol. Here, a = 10
d = 7 - 10 = - 3
Tn = (- 62)
∴ Using Tn = a + (n - 1) d, we have
- 62 = 10 + (n - 1) × (- 3)
⇒ n − 1 = −62 − 10−3 = −72−3 = 24
⇒ n = 24 + 1 = 25
⇒ Number of terms = 25
∴ Middle term = n + 12 th term
= 25 + 12 th term
= 13th term
Now T13 = 10 + 12d
= 10 + 12 (- 3)
= 10 - 36 = - 26
Thus, the middle term = - 26.
Q13. Find the sum of all three digit numbers which are divisible by 7.
Sol. The three digit numbers which are divisible by 7 are:
105, 112, 119, ....., 994.
It is an A.P. such that
a = 105
d = 112 - 105 = 7
Tn = 994 = l
∵ Tn = a + (n - 1) × d
∴ 994 = 105 + (n - 1) × 7
⇒ n − 1 = 994 − 1057 = 8897 = 127
⇒ n = 127 + 1 = 128
Now, using Sn = n/2 [a + l]
We have S128 = 128/2[105 + 994]
= 64 [1099]
= 70336
Thus, the required sum = 70336.
Q14. Find the sum of all the three digit numbers which are divisible by 9.
Sol. All the three digit numbers divisible by 9 are:
117, 126, ....., 999 and they form an A.P.
Here, a = 108
d = 117 - 108 = 9
Tn = 999 = l
Now, using Tn = a + (n - 1) d, we have
999 = 108 + (n - 1) (9)
⇒ 999 - 108 = (n - 1) × 9
⇒ 891 = (n - 1) × 9
⇒ n - 1 = 891/9 = 99
⇒ n = 99 + 1 = 100
Now, the sum of n term of an A.P. is given
Sn = n/2 [a + l]
∴ S100 = 100/2[108 + 999]
= 50 [1107]
= 55350
Thus, the required sum is 55350.
Q15. Find the sum of all the three digit numbers which are divisible by 11.
Sol. All the three digit numbers divisible by 11 are 110, 121, 132, ....., 990.
Here, a = 110
d = 121 - 110 = 11
Tn = 990
∴ Using Tn = a + (n - 1) d, we have
990 = 110 + (n - 1) × 11
⇒ n − 1 = 990 − 11011 = 80
⇒ n = 80 + 1 = 81
Now, using Sn = n/2 [a + l], we have
S81 = 81/2 [110 + 990]
= 812 [1100]
= 81 × 550 = 44550
Thus, the required sum = 44550.
Q16. The sum of the first six terms of an AP is 42. The ratio of the 10th term to its 30th term is 1:3. Calculate the first term and 13th term of A.P.
Sol. ∵ 
S6 = 62 {2a + (6 − 1)d} = 4
∴ 6a + 15d = 4 2 ...(1)
Also, (a10) : (a30) = 1 : 3
or a + 9da + 29d = 13
⇒ 3(a + 9d) = a + 29d
⇒ 3a + 27d = a + 27d
⇒ 2a = 2 d
⇒ a = d ...(2)
From (1) 6d + 15d = 42 ⇒ d = 2
From (2) a = d ⇒ d = 2
Now, a13 = a + 12d
= 2 + 12 × 2 = 26
Q17. If Sn the sum of n terms of an A.P. is given by Sn = 3n2 - 4n, find the nth term.
Sol. We have:
Sn - 1 = 3 (n - 1)2 - 4 (n - 1)
= 3 (n2 - 2n + 1) - 4n + 4
= 3n2 - 6n + 3 - 4n + 4
= 3n2 - 10n + 7
∵ nth term = Sn - Sn - 1
= 3n2 - 4n - [3n2 - 10n + 7]
= 3n2 - 4n - 3n2 + 10n - 7
= 6n - 7.
Q18. The sum of 4th and 8th terms of an A.P. is 24, and the sum of 6th and 10th terms is 44. Find the A.P.
Sol. Let, the first term = a
Common difference be = d
∴ Using Tn = a + (n - 1) d, we have
T4 = a + 3d
T6 = a + 5d
T8 = a + 7d
T10 = a + 9d
∵ T4 + T8 = 24
∴ (a + 3d) + (a + 7d) = 24
⇒ 2a + 10d = 24
⇒ a + 5d = 12
[Dividing by 2] ...(1)
Also T6 + T10 = 44
∴ (a + 5d) + (a + 9d) = 44
⇒ 2a + 14d = 44
⇒ a + 7d = 22
[Dividing by 2] ...(2)
Subtracting (1) from (2), we have:
(a + 7d) - (a + 5d) = 22 - 12
⇒ 2d = 10 ⇒ d = 5
From (1), a + 5 (5) = 12
⇒ a = 12 - 25 = - 13
Since, the A.P. is given by:
a, a + d, a + 2d, .....
∴ We have the required A.P. as:
- 13, (- 13 + 5), [- 13 + 2 (5)], .....
or - 13, - 8, - 3, .....
Q19. If Sn, the sum of first n terms of an A.P. is given by
Sn = 5n2 + 3n
Then find the nth term.
Sol. ∵ Sn = 5n2 + 3n
∴ Sn - 1 = 5 (n - 1)2 + 3 (n - 1)
= 5 (n2 - 2n + 1) + 3 (n - 1)
= 5n2 - 10n + 5 + 3n - 3
= 5n2 - 7n + 2
Now, nth term = Sn - Sn - 1
∴ The required nth term
= [5n2 + 3n] - [5n2 - 7n + 2]
= 10n - 2.
Q20. The sum of 5th and 9th terms of an A.P. is 72 and the sum of 7th and 12th term of 97. Find the A.P.
Sol. Let ‘a’ be the 1st term and ‘d’ be the common difference of the A.P.
Now, using Tn = a + (n - 1) d, we have
T5 = a + 4d
T7 = a + 6d
T9 = a + 8d
T12 = a + 11d
∵ T5 + T9 = 72
∴ a + 4d + a + 8d = 72
⇒ 2a + 12d = 72
⇒ a + 6d = 36
[Dividing by 2] ...(1)
Also T7 + T12= a + 6d + a + 11d = 97
⇒ 36 + a + 11d = 97 [From (1)]
⇒ a + 11d = 97 - 36
⇒ a + 11d = 61 ...(2)
Subtracting (1) from (2), we get
a + 11d - a - 6d = 61 - 36
⇒ 5d = 25
⇒ d = 25/5
From (1), we have
a + 11 (5) = 61
a + 55 = 61
⇒ a = 61 - 55 = 6
Now, an A.P. is given by
a, a + d, a + 2d, a + 3d, .....
∴ The required A.P. is:
6, (6 + 5), [6 + 2 (5)], [6 + 3 (5)], .....
or 6, 11, 16, 24, .....
Q21. In an A.P. the sum of its first ten terms is –150 and the sum of its next term is –550. Find the A.P.
Sol. Let the first term = a
And the common difference = d
∴ S1010 = 102 [2a + (10 − 1)d] = −150 ⇒ 10a + 45d = –150⇒ 2a + 9d = –30 ...(1)∵ The sum of next 10 terms
(i.e. S20 – S10) = –550
∴ 202 [2a + (20 − 1)d] + (−150) = −550 ⇒ 20a + 190d + 150 = –550⇒ 2a + 19d + 15 = –55⇒ 2a + 19d = – 55 – 15
⇒ 2a + 19d = –70 ...(2)
Subtracting (1) from (2), we get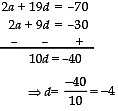 From (1), 2(a) + 9(–4) = –30 or a = 6/2 = 3Thus, AP is a, a + d, a + 2d ...or 3, [3 + (–4)], [3 + 2(–4)], ...
From (1), 2(a) + 9(–4) = –30 or a = 6/2 = 3Thus, AP is a, a + d, a + 2d ...or 3, [3 + (–4)], [3 + 2(–4)], ...
or 3, –1, –5, ...
Q22. Which term of the A.P. 3, 15, 27, 39, ..... will be 120 more than its 21st term?
Sol. Let the 1st term is ‘a’ and common difference = d
∴ a = 3 and d = 15 - 3 = 12
Now, using Tn = a + (n - 1) d
∴ T21 = 3 + (21 - 1) × 12
= 3 + 20 × 12
= 3 + 240 = 243
Let the required term be the nth term.
∵ nth term = 120 + 21st term
= 120 + 243 = 363
Now Tn = a + (n - 1) d
⇒ 363 = 3 + (n - 1) × 12
⇒ 363 - 3 = (n - 1) × 12
⇒ n - 1 = 360/12 = 30
⇒ n = 30 + 1 = 31
Thus the required term is the 31st term of the A.P.
Q23. Which term of the A.P. 4, 12, 20, 28, ..... will be 120 more than its 21st term?
Sol. Here, a = 4
d = 12 - 4 = 8
Using Tn = a + (n - 1) d
∴ T21 = 4 + (21 - 1) × 8
= 4 + 20 × 8 = 164
∵ The required nth term = T21 + 120
∴ nth term = 164 + 120 = 284
∴ 284 = a + (n - 1) d
⇒ 284 = 4 + (n - 1) × 8
⇒ 284 - 4 = (n - 1) × 8
⇒ n - 1 = 280/8 = 35
⇒ n = 35 + 1 = 36
Thus, the required term is the 36th term of the A.P.
Q24. The sum of n terms of an A.P. is 5n2 - 3n. Find the A.P. Hence find its 10th term.
Sol. We have:
Sn = 5n2 - 3n
∴ S1 = 5 (1)2 - 3 (1) = 2
⇒ First term T1 = (a) = 2
S2 = 5 (2)2 - 3 (2)
= 20 - 6 = 14
⇒ Second term T2 = 14 - 2 = 12
Now the common difference = T2 - T1
⇒ d = 12 - 2 = 10
∵ An A.P. is given by
a, (a + d), (a + 2d) .....
∴ The required A.P. is:
2, (2 + 10), [2 + 2 (10)], .....
⇒ 2, 12, 22, .....
Now, using Tn = a + (n - 1) d, we have
T10 = 2 + (10 - 1) × 10
= 2 + 9 × 10
= 2 + 90 = 92.
Q25. Find the 10th term from the end of the A.P.:
8, 10, 12, ....., 126
Sol. Here, a = 8
d = 10 - 8 = 2
Tn = 126
Using Tn = a + (n - 1) d
⇒ 126 = 8 + (n - 1) × 2
⇒ n - 1 =
⇒ n = 59 + 1 = 60
∴ l = 60
Now 10th term from the end is given by
l - (10 - 1) = 60 - 9 = 51
Now, T51 = a + 50d
= 8 + 50 × 2
= 8 + 100 = 108
Thus, the 10th term from the end is 108.
Q26. The sum of n terms of an A.P. is 3n2 + 5n. Find the A.P. Hence, find its 16th term.
Sol. We have,
Sn = 3n2 + 5n
∴ S1 = 3 (1)2 + 5 (1)
= 3 + 5 = 8
⇒ T1 = 8 ⇒ a = 8
S2 = 3 (2)2 + 5 (2)
= 12 + 10 = 22
⇒ T2 = 22 - 8 = 14
Now d = T2 - T1 = 14 - 8 = 6
∵ An A.P. is given by,
a, (a + d), (a + 2d), .....
∴ The required A.P. is:
8, (8 + 6), [8 + 2 (6)], .....
⇒ 8, 14, 20, .....
Now, using Tn = a + (n - 1) d, we hve
T16 = a + 15d
= 8 + 15 × 6 = 98
Thus, the 16th term of the A.P. is 98.
Q27. In an AP, the sum of first n-terms is 3n22 + 13n2. Find the 25th term.
Sol. We know that: an = Sn - Sn-1, where,
Sn = 3n2 + 13n2
∴ S25 = 3(25)2 + 13(25)2 and S24 = 3(24)2 + 13(24)2
Now, a25 = S25 - S24
a25 = 12 [3(252 - 242) + 13(25 - 24)]
⇒ a25 = 12 [49 × 3 + 13]
⇒ a25 = 12 [147 + 13]
⇒ a25 = 12 [160] = 80
Q28. The sum of 4th and 8th terms of an A.P. is 24 and the sum of 6th and 10th terms is 44. Find the first three terms of the A.P.
Sol. Let the first term be ‘a’ and the common difference be ‘d’.
Using Tn = a + (n - 1) d, we have
T4 = a + 3d, T6 = a + 5d
T8 = a + 7d and T10 = a + 9d
Since T4 + T8 = 24
∴ a + 3d + a + 7d = 24
⇒ 2a + 10d = 24 ⇒ a + 5d = 12 ...(1)
Also, T6 + T10 = 44
∴ a + 5d + a + 9d = 44
⇒ 2a + 14d = 44 ⇒ a + 7d = 22 ...(2)
Subtracting (2) from (1), we get,
a + 7d - a - 5d = 22 - 12
⇒ 2d = 10 ⇒ d = 5
Now from (1),
a + 5 (5) = 12
⇒ a + 25 = 12 ⇒ a = - 13
∴ First term (T1) = a + 0 = - 13
Second term (T2) = a + d
= - 13 + 5 = - 8
Third term T3 = - a + 2d
= - 13 + 10 = - 3
Q29. In an A.P., the first term is 8, nth term is 33 and sum of first n terms is 123. Find n and d, the common difference.
Sol. Here,
First term T1 = 8 ⇒ a = 8
nth term Tn = 33 = l
∵ Sn = 123 [Given]
∴ Using, Sn = n/2 [a + l], we have
Sn = n/2 [8 + 33]
⇒123 = n2 × 41 ⇒ n = 123 × 241 = 6 Now, T6 = 33
⇒ a + 5d = 33
⇒ 8 + 5d = 33
⇒ 5d = 33 - 8 = 25
⇒ d = 25/5 = 5
Thus, n = 6 and d = 5.
Q30. For what value of n are the nth terms of two A.P.’s 63, 65, 67, ..... and 3, 10, 17, ..... equal?
Sol. For the 1st A.P.
a = 63
d = 65 - 63 = 2
∴ Tn = a + (n - 1) d
⇒ Tn = 63 + (n - 1) × 2
For the 2nd A.P.
a = 3
d = 10 - 3 = 7
∴ Tn = a + (n - 1) d
⇒ Tn = 3 + (n - 1) × 7
∵ [Tn of 1st A.P.] = [Tn of 2nd A.P.]
∴ 63 + (n - 1) × 2 = 3 + (n - 1) × 7
⇒ 63 - 3 + (n - 1) × 2 = (n - 1) 7
⇒ 60 + (n - 1) × 2 - (n - 1) × 7 = 0
⇒ 60 + (n - 1) [2 - 7] = 0
⇒ 60 + (n - 1) × (- 5) = 0
⇒ (n - 1) = -60/-5 = 12
⇒ n = 12 + 1 = 13
Thus, the required value of n is 13.
Q31. If m times the mth term of an A.P. is equal to n times the nth term, find the (m + n)th term of the A.P.
Sol. Let the first term (T1) = a and the common difference be ‘d’.
∴ nth term = a + (n - 1) d
And mth term = a + (m - 1) d
Also,
(m + n)th term = a + (m + n - 1) d ...(1)
∵ m (mth term) = n (nth term)
∴ m [a + (m - 1) d] = n [a + (n - 1) d]
⇒ ma + m (m - 1) d = na + n (n - 1) d
⇒ ma + (m2 - m) d - na - (n2 - n) d = 0
⇒ ma - na + (m2 - m) d - (n2 - n) d = 0
⇒ a [m - n] + [m2 - m - n2 + n] d = 0
⇒ a [m - n] + [(m2 - n2) - (m - n)] d = 0
⇒ a [m - n] + [(m + n) (m - n) - (m - n)] d = 0
⇒ a [m - n] + (m - n) [m + n - 1] d = 0
Dividing throughout by (m - n), we have:
a + [m + n - 1] d = 0
⇒ a + [(m + n) - 1] d = 0 ...(2)
⇒ (m + n) th term = 0 [From (1) and (2)]
Q32. In an A.P., the first term is 25, nth term is - 17 and sum of first n terms is 60. Find ‘n’ and ‘d’, the common difference.
Sol. Here, the first term a = 25
And the nth term = - 17 = l
Using Tn = a + (n - 1) d, we have:
- 17 = 25 + (n - 1) d
⇒ (n - 1) d = - 17 - 25 = - 42
⇒ (n − 1) d = −42 ⇒ d = −42n − 1 ...(1)
Also, Sn = n/2 [a + l]
⇒ 60 = n/2 [25 + (- 17)]
⇒ 60 = n2 [8] ⇒ 60 = 4n ⇒ n = 60/4 = 15From (1), we have d = −4215 − 1 = −4214 = −3
Thus, n = 15 and d = - 3
Q33. In an A.P., the first term is 22, nth term is - 11 and sum of first n terms is 66. Find n and d, the common difference.
Sol. We have
1st term (T1) = 22 ⇒ a = 22
Last term (Tn) = - 11 ⇒ l = - 11
Using, Sn = n/2 [a + l], we have:
66 = n/2 [22 + (- 11)]
⇒ 66 × 2 = n [11]
⇒ n = 66 × 211 = 12
Again using Tn = a + (n - 1) d
We have:
T12 = 22 + (12 - 1) × d
- 11 = 22 + 11d [∵ nth term = - 11]
⇒ 11d = - 22 - 11 = - 33
⇒ d = -33/11 = -3
Thus, n = 12 and d = - 3
|
126 videos|457 docs|75 tests
|
FAQs on Class 10 Maths Chapter 5 Question Answers - Arithmetic Progressions - 1
| 1. What is an arithmetic progression? |  |
| 2. How do you find the nth term of an arithmetic progression? |  |
| 3. How can you determine if a given sequence is an arithmetic progression? |  |
| 4. What is the sum of the first n terms of an arithmetic progression? |  |
| 5. How can arithmetic progressions be applied in real-life scenarios? |  |

|
Explore Courses for Class 10 exam
|

|


















