NCERT Solutions for Class 10 Maths Chapter 9 - Some Applications of Trigonometry (Exercise 9.1) - 1
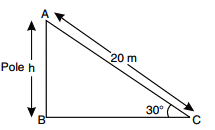
Q1. A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30° (see figure).
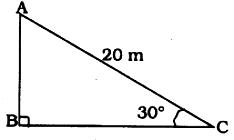 Ans: Given: length of the rope (AC) = 20 m, ∠ACB = 30°
Ans: Given: length of the rope (AC) = 20 m, ∠ACB = 30°
Let the height of the pole (AB) = h metre
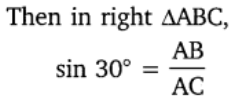
⇒ h/20 = 1/2⇒ h = 20/2 = 10 m
Hence, height of the pole = 10 m
Q2. A tree breaks due to a storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
Ans: Let DB is a tree and AD is the broken part of it that touches the ground at C.
 Given: ∠ACB = 30º
Given: ∠ACB = 30º
and BC = 8m
Let AB = x m
and AD = y m
∴ Now, length of the tree
= (x + y) m
In Δ ABC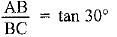
⇒ 
⇒ 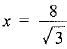 ... (i)
... (i)
Hence, total height of the tree = 
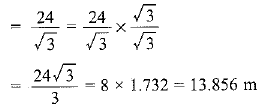
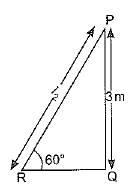
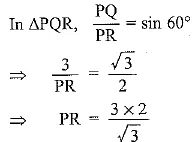
Q3. A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for older children, she wants to have a steep slide at a height of 3 m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
Ans: Let l1 is the length of the slide for children below the age of 5 years and l2 is the length of the slide for elder children.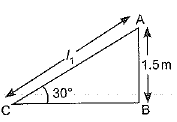 In ΔABC
In ΔABC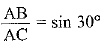
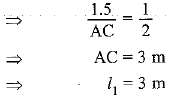

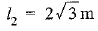
Q4. The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
Ans: Let h be the height of the tower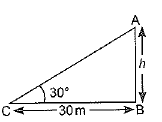 ⇒
⇒ 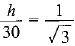
⇒ 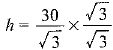
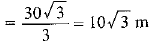
Q5. A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
Ans: Given: height AB = 60 m, ∠ACB = 60°, AC = length of the string
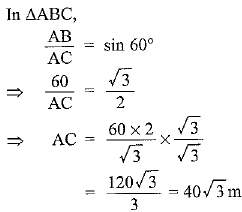
Hence, the length of the string = 40√3 m
Q6. A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
Ans: Let AB = height of the building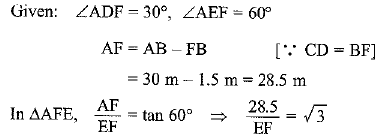
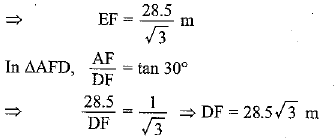
The distance walked by the boy towards building
DE = DF - EF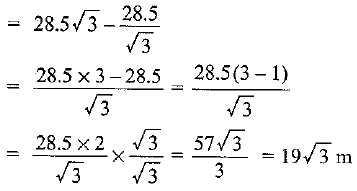
Q7. From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.
Ans: Given: AB = 20 m (Height of the building)
Let AD = h m (Height of the tower)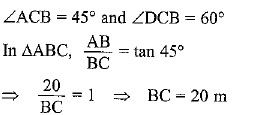
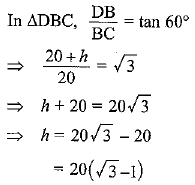
Hence, height of the tower = 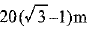
Q8. A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
Ans: Let the height of the pedestal AB = h m
Given: height of the statue = 1.6 m, ∠ACB = 45° and ∠DCB = 60°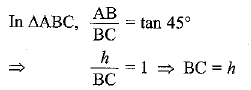
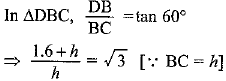
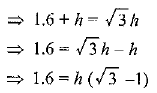
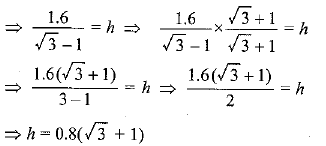
Hence, height of the pedestal 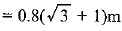
|
276 docs|155 tests
|

















