NCERT Solutions for Class 10 Maths Chapter 8 - Introduction to Trigonometry (Exercise 8.2)
Q1. Evaluate the following:
(i) sin 60° cos 30° + sin 30° cos 60°
(ii) 2 tan2 45° + cos2 30° – sin2 60
Solution:
(i) The values of the given trigonometric ratios:
sin 30° = 1/2, cos 30° = √3/2, sin 60° = 3/2, cos 60°= 1/2
Now, substitute the values in the given problem
sin 60° cos 30° + sin 30° cos 60° = √3/2 ×√3/2 + (1/2) ×(1/2 ) = 3/4+1/4 = 4/4 = 1
(ii) The values of the trigonometric ratios:
sin 60° = √3/2, cos 30° = √3/2, tan 45° = 1
Substitute the values in the given problem
2 tan2 45° + cos2 30° – sin2 60 = 2(1)2 + (√3/2)2-(√3/2)2 = 2 + 0 = 2
(iii) We know that:
cos 45° = 1/√2, sec 30° = 2/√3, cosec 30° = 2
Substitute the values, we get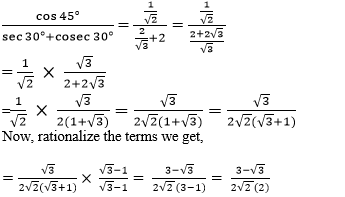
Now, multiply both the numerator and denominator by √2, we get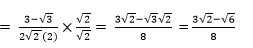
Therefore, cos 45°/(sec 30°+cosec 30°) = (3√2 – √6)/8
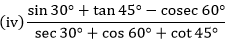
We know that,
sin 30° = 1/2, tan 45° = 1, cosec 60° = 2/√3, sec 30° = 2/√3, cos 60° = 1/2, cot 45° = 1
Substitute the values in the given problem, we get
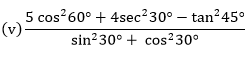
We know that,
cos 60° = 1/2, sec 30° = 2/√3, tan 45° = 1, sin 30° = 1/2, cos 30° = √3/2
Now, substitute the values in the given problem, we get
(5cos260° + 4sec230° – tan245°)/(sin2 30° + cos2 30°)
= 5(1/2)2 + 4(2/√3)2 - 12/(1/2)2 + (√3/2)2 = (5/4 + 16/3 - 1)/(1/4 + 3/4) = {(15 + 64 - 12)/12}/(4/4) = 67/12
Q2. Choose the correct option and justify your choice:
(i) 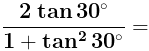
(a) sin 60°
(b) cos 60°
(c) tan 60°
(d) sin 30°
Ans. (A) is correct
Justification: Substitute tan 30° = 1/√3 in the given equation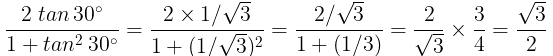
∵ √3/2 = sin 60°
The obtained solution is equivalent to the trigonometric ratio sin 60°
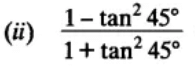
(a) tan 90°
(b) 1
(c) sin 45°
(d) 0
Ans. (D) is correct
Justification:
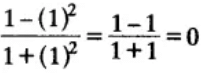
(iii) sin 2A = 2 sin A is true when A =
(a) 0°
(b) 30°
(c) 45°
(d) 60°
Ans. (A) is correct.
Justification: To find the value of A, substitute the degree given in the options one by one
sin 2A = 2 sin A is true when A = 0°
As, sin 2A = sin 0° = 0 and 2 sin A = 2 sin 0° = 2 × 0 = 0
or,
Apply the sin 2A formula, to find the degree value
sin 2A = 2sin A cos A
⇒ 2sin A cos A = 2 sin A
⇒ 2cos A = 2 ⇒ cos A = 1
Now, we have to check, to get the solution as 1, which degree value has to be applied.
When 0 degree is applied to cos value, i.e., cos 0 = 1
Therefore, ⇒ A = 0°
(iv) 
(a) cos 60°
(b) sin 60°
(c) tan 60°
(d) sin 30°
Ans. (C) is correct.
Justification: 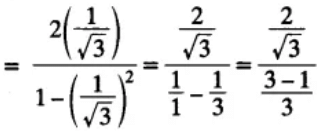
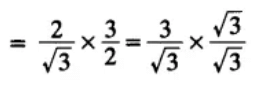
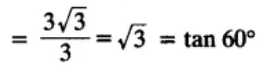
Q3. If tan (A + B) = √3 and tan (A – B) = 1/√3 ,0° < A + B ≤ 90°; A > B, find A and B.
Solution:
tan (A + B) = √3
Since √3 = tan 60°
Now substitute the degree value
⇒ tan (A + B) = tan 60°
(A + B) = 60° … (i)
The above equation is assumed as equation (i)
tan (A – B) = 1/√3
Since 1/√3 = tan 30°
Now substitute the degree value
⇒ tan (A – B) = tan 30°
(A – B) = 30° … equation (ii)
Now add the equation (i) and (ii), we get
A + B + A – B = 60° + 30°
Cancel the terms B
2A = 90°
A= 45°
Now, substitute the value of A in equation (i) to find the value of B
45° + B = 60°
B = 60° – 45°
B = 15°
Therefore A = 45° and B = 15°
Q4. State whether the following are true or false. Justify your answer.
(i) sin (A + B) = sin A + sin B.
Ans. False
Justification: Let us take A = 30° and B = 60°, then
Substitute the values in the sin (A + B) formula, we get
sin (A + B) = sin (30° + 60°) = sin 90° = 1 and,
sin A + sin B = sin 30° + sin 60°
= 1/2 + √3/2 = 1+√3/2
Since the values obtained are not equal, the solution is false.
(ii) The value of sin θ increases as θ increases.
Ans. True
Justification: According to the values obtained as per the unit circle, the values of sin are: sin 0° = 0, sin 30° = 1/2, sin 45° = 1/√2, sin 60° = √3/2, sin 90° = 1
Thus the value of sin θ increases as θ increases. Hence, the statement is true
(iii) The value of cos θ increases as θ increases.
Ans. False
Justification: According to the values obtained as per the unit circle, the values of cos are: cos 0° = 1, cos 30° = √3/2, cos 45° = 1/√2, cos 60° = 1/2, cos 90° = 0
Thus, the value of cos θ decreases as θ increases. So, the statement given above is false.
(iv) sin θ = cos θ for all values of θ.
Ans. False
Justification: sin θ = cos θ, when a right triangle has 2 angles of (π/4). Therefore, the above statement is false.
(v) cot A is not defined for A = 0°.
Ans. True
Justification: Since cot function is the reciprocal of the tan function, it is also written as:
cot A = cos A/sin A
Now substitute A = 0°
cot 0° = cos 0°/sin 0° = 1/0 = undefined.
Hence, it is true
|
70 videos|242 docs|187 tests
|

















