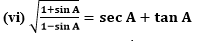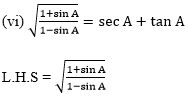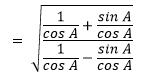Q1. Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.
Solution:
To convert the given trigonometric ratios in terms of cot functions, use trigonometric formulas
We know that,
cosec2A – cot2A = 1
cosec2A = 1 + cot2A
Since cosec function is the inverse of sin function, it is written as
1/sin2A = 1 + cot2A
Now, rearrange the terms, it becomes
sin2A = 1/(1+cot2A)
Now, take square roots on both sides, we get
sin A = ±1/(√(1+cot2A)
The above equation defines the sin function in terms of cot function
Now, to express sec function in terms of cot function, use this formula
sin2A = 1/ (1+cot2A)
Now, represent the sin function as cos function
1 – cos2A = 1/ (1+cot2A)
Rearrange the terms,
cos2A = 1 – 1/(1+cot2A)
⇒cos2A = (1-1+cot2A)/(1+cot2A)
Since sec function is the inverse of cos function,
⇒ 1/sec2A = cot2A/(1+cot2A)
Take the reciprocal and square roots on both sides, we get
⇒ sec A = ±√ (1+cot2A)/cotA
Now, to express tan function in terms of cot function
tan A = sin A/cos A and cot A = cos A/sin A
Since cot function is the inverse of tan function, it is rewritten as
tan A = 1/cot A
Q2. Write all the other trigonometric ratios of ∠A in terms of sec A.
Solution:
Cos A function in terms of sec A:
sec A = 1/cos A
⇒ cos A = 1/sec A
sec A function in terms of sec A:
cos2A + sin2A = 1
Rearrange the terms
sin2A = 1 – cos2A
sin2A = 1 – (1/sec2A)
sin2A = (sec2A-1)/sec2A
sin A = ± √(sec2A-1)/sec A
cosec A function in terms of sec A:
sin A = 1/cosec A
⇒cosec A = 1/sin A
cosec A = ± sec A/√(sec2A-1)
Now, tan A function in terms of sec A:
sec2A – tan2A = 1
Rearrange the terms
⇒ tan2A = sec2A + 1
tan A = √(sec2A + 1)
cot A function in terms of sec A:
tan A = 1/cot A
⇒ cot A = 1/tan A
cot A = ±1/√(sec2A + 1)
Q3. Evaluate:
(i) (sin263° + sin227°)/(cos217° + cos273°)
(ii) sin 25° cos 65° + cos 25° sin 65°
Solution:
(i) (sin263° + sin227°)/(cos217° + cos273°)
To simplify this, convert some of the sin functions into cos functions and cos function into sin function and it becomes,
= [sin2(90°-27°) + sin227°] / [cos2(90°-73°) + cos273°)]
= (cos227° + sin227°)/(sin227° + cos273°)
= 1/1 =1 (since sin2A + cos2A = 1)
Therefore, (sin263° + sin227°)/(cos217° + cos273°) = 1
(ii) sin 25° cos 65° + cos 25° sin 65°
To simplify this, convert some of the sin functions into cos functions and cos function into sin function and it becomes,
= sin(90°-25°) cos 65° + cos (90°-65°) sin 65°
= cos 65° cos 65° + sin 65° sin 65°
= cos265° + sin265° = 1 (since sin2A + cos2A = 1)
Therefore, sin 25° cos 65° + cos 25° sin 65° = 1
Q4. Choose the correct option. Justify your choice.
(i) 9 sec2A – 9 tan2A =
(a) 1
(b) 9
(c) 8
(d) 0
(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ)
(a) 0
(b) 1
(c) 2
(d) – 1
(iii) (sec A + tan A) (1 – sin A) =
(a) sec A
(b) sin A
(c) cosec A
(d) cos A
(iv) 1+tan2A/1+cot2A =
(a) sec2 A
(b) -1
(c) cot2A
(d) tan2A
Solution:
(i) (B) is correct.
Justification:
Take 9 outside, and it becomes
9 sec2A – 9 tan2A
= 9 (sec2A – tan2A)
= 9×1 = 9 (∵ sec2 A – tan2 A = 1)
Therefore, 9 sec2A – 9 tan2A = 9
(ii) (C) is correct
Justification:
(1 + tan θ + sec θ) (1 + cot θ – cosec θ)
We know that, tan θ = sin θ/cos θ
sec θ = 1/ cos θ
cot θ = cos θ/sin θ
cosec θ = 1/sin θ
Now, substitute the above values in the given problem, we get
= (1 + sin θ/cos θ + 1/ cos θ) (1 + cos θ/sin θ – 1/sin θ)
Simplify the above equation,
= (cos θ +sin θ+1)/cos θ × (sin θ+cos θ-1)/sin θ
= (cos θ+sin θ)2-12/(cos θ sin θ)
= (cos2θ + sin2θ + 2cos θ sin θ -1)/(cos θ sin θ)
= (1+ 2cos θ sin θ -1)/(cos θ sin θ) (Since cos2θ + sin2θ = 1)
= (2cos θ sin θ)/(cos θ sin θ) = 2
Therefore, (1 + tan θ + sec θ) (1 + cot θ – cosec θ) =2
(iii) (D) is correct.
Justification:
We know that,
Sec A= 1/cos A
Tan A = sin A / cos A
Now, substitute the above values in the given problem, we get
(secA + tanA) (1 – sinA)
= (1/cos A + sin A/cos A) (1 – sinA)
= (1+sin A/cos A) (1 – sinA)
= (1 – sin2A)/cos A
= cos2A/cos A = cos A
Therefore, (secA + tanA) (1 – sinA) = cos A
(iv) (D) is correct.
Justification:
We know that,
tan2A =1/cot2A
Now, substitute this in the given problem, we get
1+tan2A/1+cot2A
= (1+1/cot2A)/1+cot2A
= (cot2A+1/cot2A)×(1/1+cot2A)
= 1/cot2A = tan2A
So, 1+tan2A/1+cot2A = tan2A
Q5. Prove the following identities, where the angles involved are acute angles for which the expressions are defined.
(i) (cosec θ – cot θ)2 = (1-cos θ)/(1+cos θ)
(ii) cos A/(1+sin A) + (1+sin A)/cos A = 2 sec A
(iii) tan θ/(1-cot θ) + cot θ/(1-tan θ) = 1 + sec θ cosec θ
[Hint : Write the expression in terms of sin θ and cos θ]
(iv) (1 + sec A)/sec A = sin2A/(1-cos A)
[Hint : Simplify LHS and RHS separately]
(v) ( cos A–sin A+1)/( cos A +sin A–1) = cosec A + cot A, using the identity cosec2A = 1+cot2A.
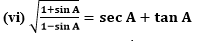
(vii) (sin θ – 2sin3θ)/(2cos3θ-cos θ) = tan θ
(viii) (sin A + cosec A)2 + (cos A + sec A)2 = 7+tan2A+cot2A
(ix) (cosec A – sin A)(sec A – cos A) = 1/(tan A+cotA)
[Hint : Simplify LHS and RHS separately]
(x) (1+tan2A/1+cot2A) = (1-tan A/1-cot A)2 = tan2A
Solution:
(i) (cosec θ – cot θ)2 = (1-cos θ)/(1+cos θ)
To prove this, first take the Left-Hand side (L.H.S) of the given equation, to prove the Right Hand Side (R.H.S)
L.H.S. = (cosec θ – cot θ)2
The above equation is in the form of (a-b)2, and expand it
Since (a-b)2 = a2 + b2 – 2ab
Here a = cosec θ and b = cot θ
= (cosec2θ + cot2θ – 2cosec θ cot θ)
Now, apply the corresponding inverse functions and equivalent ratios to simplify
= (1/sin2θ + cos2θ/sin2θ – 2cos θ/sin2θ)
= (1 + cos2θ – 2cos θ)/(1 – cos2θ)
= (1-cos θ)2/(1 – cosθ)(1+cos θ)
= (1-cos θ)/(1+cos θ) = R.H.S.
Therefore, (cosec θ – cot θ)2 = (1-cos θ)/(1+cos θ)
Hence proved.
(ii) (cos A/(1+sin A)) + ((1+sin A)/cos A) = 2 sec A
Now, take the L.H.S of the given equation.
L.H.S. = (cos A/(1+sin A)) + ((1+sin A)/cos A)
= [cos2A + (1+sin A)2]/(1+sin A)cos A
= (cos2A + sin2A + 1 + 2sin A)/(1+sin A) cos A
Since cos2A + sin2A = 1, we can write it as
= (1 + 1 + 2sin A)/(1+sin A) cos A
= (2+ 2sin A)/(1+sin A)cos A
= 2(1+sin A)/(1+sin A)cos A
= 2/cos A = 2 sec A = R.H.S.
L.H.S. = R.H.S.
(cos A/(1+sin A)) + ((1+sin A)/cos A) = 2 sec A
Hence proved.
(iii) tan θ/(1-cot θ) + cot θ/(1-tan θ) = 1 + sec θ cosec θ
L.H.S. = tan θ/(1-cot θ) + cot θ/(1-tan θ)
We know that tan θ =sin θ/cos θ
cot θ = cos θ/sin θ
Now, substitute it in the given equation, to convert it in a simplified form
= [(sin θ/cos θ)/1-(cos θ/sin θ)] + [(cos θ/sin θ)/1-(sin θ/cos θ)]
= [(sin θ/cos θ)/(sin θ-cos θ)/sin θ] + [(cos θ/sin θ)/(cos θ-sin θ)/cos θ]
= sin2θ/[cos θ(sin θ-cos θ)] + cos2θ/[sin θ(cos θ-sin θ)]
= sin2θ/[cos θ(sin θ-cos θ)] – cos2θ/[sin θ(sin θ-cos θ)]
= 1/(sin θ-cos θ) [(sin2θ/cos θ) – (cos2θ/sin θ)]
= 1/(sin θ-cos θ) × [(sin3θ – cos3θ)/sin θ cos θ]
= [(sin θ-cos θ)(sin2θ+cos2θ+sin θ cos θ)]/[(sin θ-cos θ)sin θ cos θ]
= (1 + sin θ cos θ)/sin θ cos θ
= 1/sin θ cos θ + 1
= 1 + sec θ cosec θ = R.H.S.
Therefore, L.H.S. = R.H.S.
Hence proved
(iv) (1 + sec A)/sec A = sin2A/(1-cos A)
First find the simplified form of L.H.S
L.H.S. = (1 + sec A)/sec A
Since secant function is the inverse function of cos function and it is written as
= (1 + 1/cos A)/1/cos A
= (cos A + 1)/cos A/1/cos A
Therefore, (1 + sec A)/sec A = cos A + 1
R.H.S. = sin2A/(1-cos A)
We know that sin2A = (1 – cos2A), we get
= (1 – cos2A)/(1-cos A)
= (1-cos A)(1+cos A)/(1-cos A)
Therefore, sin2A/(1-cos A)= cos A + 1
L.H.S. = R.H.S.
Hence proved
(v) (cos A–sin A+1)/(cos A+sin A–1) = cosec A + cot A, using the identity cosec2A = 1+cot2A.
With the help of identity function, cosec2A = 1+cot2A, let us prove the above equation.
L.H.S. = (cos A–sin A+1)/(cos A+sin A–1)
Divide the numerator and denominator by sin A, we get
= (cos A–sin A+1)/sin A/(cos A+sin A–1)/sin A
We know that cos A/sin A = cot A and 1/sin A = cosec A
= (cot A – 1 + cosec A)/(cot A+ 1 – cosec A)
= (cot A – cosec2A + cot2A + cosec A)/(cot A+ 1 – cosec A) (using cosec2A – cot2A = 1
= [(cot A + cosec A) – (cosec2A – cot2A)]/(cot A+ 1 – cosec A)
= [(cot A + cosec A) – (cosec A + cot A)(cosec A – cot A)]/(1 – cosec A + cot A)
= (cot A + cosec A)(1 – cosec A + cot A)/(1 – cosec A + cot A)
= cot A + cosec A = R.H.S.
Therefore, (cos A–sin A+1)/(cos A+sin A–1) = cosec A + cot A
Hence Proved
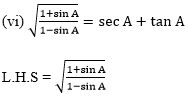
First divide the numerator and denominator of L.H.S. by cos A,
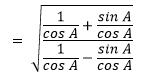
We know that 1/cos A = sec A and sin A/ cos A = tan A and it becomes,
= √(sec A+ tan A)/(sec A-tan A)
Now using rationalization, we get
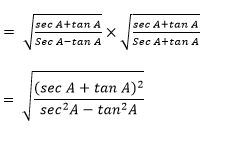
= (sec A + tan A)/1
= sec A + tan A = R.H.S
Hence proved
(vii) (sin θ – 2sin3θ)/(2cos3θ-cos θ) = tan θ
L.H.S. = (sin θ – 2sin3θ)/(2cos3θ – cos θ)
Take sin θ as in numerator and cos θ in denominator as outside, it becomes
= [sin θ(1 – 2sin2θ)]/[cos θ(2cos2θ- 1)]
We know that sin2θ = 1-cos2θ
= sin θ[1 – 2(1-cos2θ)]/[cos θ(2cos2θ -1)]
= [sin θ(2cos2θ -1)]/[cos θ(2cos2θ -1)]
= tan θ = R.H.S.
Hence proved
(viii) (sin A + cosec A)2 + (cos A + sec A)2 = 7+tan2A+cot2A
L.H.S. = (sin A + cosec A)2 + (cos A + sec A)2
It is of the form (a+b)2, expand it
(a+b)2 =a2 + b2 +2ab
= (sin2A + cosec2A + 2 sin A cosec A) + (cos2A + sec2A + 2 cos A sec A)
= (sin2A + cos2A) + 2 sin A(1/sin A) + 2 cos A(1/cos A) + 1 + tan2A + 1 + cot2A
= 1 + 2 + 2 + 2 + tan2A + cot2A
= 7+tan2A+cot2A = R.H.S.
Therefore, (sin A + cosec A)2 + (cos A + sec A)2 = 7+tan2A+cot2A
Hence proved.
(ix) (cosec A – sin A)(sec A – cos A) = 1/(tan A + cotA)
First, find the simplified form of L.H.S
L.H.S. = (cosec A – sin A)(sec A – cos A)
Now, substitute the inverse and equivalent trigonometric ratio forms
= (1/sin A – sin A)(1/cos A – cos A)
= [(1-sin2A)/sin A][(1-cos2A)/cos A]
= (cos2A/sin A)×(sin2A/cos A)
= cos A sin A
Now, simplify the R.H.S
R.H.S. = 1/(tan A+cotA)
= 1/(sin A/cos A +cos A/sin A)
= 1/[(sin2A+cos2A)/sin A cos A]
= cos A sin A
L.H.S. = R.H.S.
(cosec A – sin A)(sec A – cos A) = 1/(tan A+cotA)
Hence proved
(x) (1+tan2A/1+cot2A) = (1-tan A/1-cot A)2 = tan2A
L.H.S. = (1+tan2A/1+cot2A)
Since cot function is the inverse of tan function,
= (1+tan2A/1+1/tan2A)
= 1+tan2A/[(1+tan2A)/tan2A]
Now cancel the 1+tan2A terms, we get
= tan2A
(1+tan2A/1+cot2A) = tan2A
Similarly,
(1-tan A/1-cot A)2 = tan2A
Hence proved