Class 10 Maths Chapter 8 Question Answers - Introduction to Trigonometry
Q1: If cotθ = 7/8 then what is the value of 
Sol: 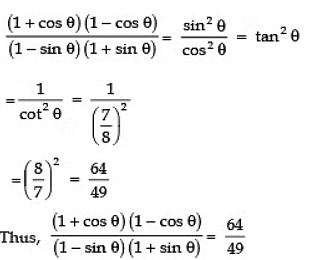
Q2: If tan A  then find sin A.
then find sin A.
Sol: In a right Δ ABC (∠B = 90°), Hypotenuse = AC, Base = AB, and Perpendicular = BC.
Since,

Using Pythagoras theorem, we have:


Q3: Evaluate cos 60°· sin 30° + sin 60°· cos 30°.
Sol: We have:
cos 60°· sin 30° + sin 60°· cos 30°

Q4: In the given figure, AC is the length of a ladder. Find it.
Sol: Let AC =x = [Length of ladder]
∴ In right Δ ABC,


Thus, the length of the ladder is 2√3 m.
Q5: If sin θ = 12/13 , find the value of:  .
.
Sol:
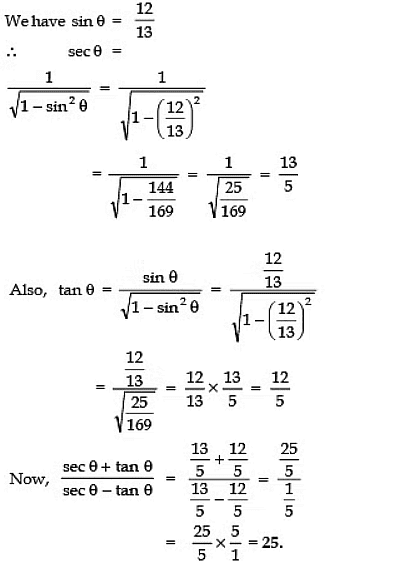 Q6: In the given figure, find BC.
Q6: In the given figure, find BC.
Sol: In Δ ABC,


Q7: In Δ ABC, if AD ⊥ BC and BD = 10 cm; ∠ B = 60° and ∠C = 30°, then find CD.
Sol: In right Δ ABD, we have


Q8: In the given figure,  find AC, if AB = 12 cm.
find AC, if AB = 12 cm.
Sol:
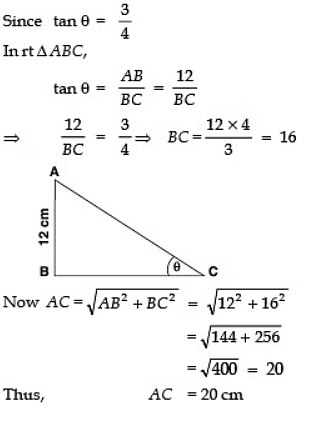
Q9: In the given figure, Δ ABC is a right triangle. Find the value of 2 sinθ − cosθ.
Sol: We have the right Δ ABC,




Q10: In the figure, find sinA.
Sol: In right Δ ABC,




Q11: Find the value of:

Sol: We have:


Q12: Write the value of: 
Sol:
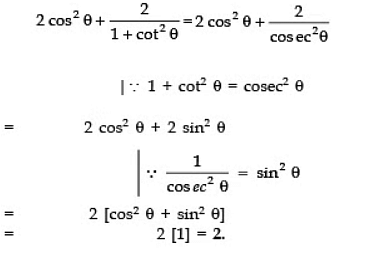
Q13: Write the value of: 
Ans:

Q14: If sec2 θ (1 + sin θ) (1 − sinθ) = k, find the value of k.
Sol:
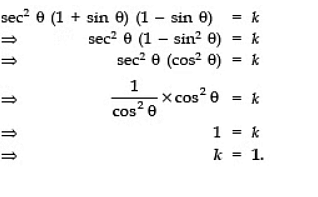
Q15: If sin  then find the value of (2 cot2 θ + 2).
then find the value of (2 cot2 θ + 2).
Sol: 2 cot2 θ + 2 = 2 (cot2 θ + 1) = 2 (cosec2 θ)


Q16: If cos A = 3/5, find 9 cot2 A − 1.



Q18: If sinθ = cosθ, find the value of θ.
Sol: We have:
sinθ = cosθ
Dividing both sides by cosθ, we get

⇒ tan θ = 1 ...(1)
From, the table, we have:
tan 45° = 1 ...(2)
From (1) and (2), we have:
θ = 45°.
|
126 videos|457 docs|75 tests
|
FAQs on Class 10 Maths Chapter 8 Question Answers - Introduction to Trigonometry
| 1. What is trigonometry? |  |
| 2. Why is trigonometry important? |  |
| 3. What are the basic trigonometric ratios? |  |
| 4. How do you find the value of trigonometric ratios? |  |
| 5. What are the applications of trigonometry in real life? |  |

|
Explore Courses for Class 10 exam
|

|


















