Class 10 Maths Chapter 8 Question Answers - Introduction to Trigonometry
Q1: It is given that tan (θ1 + θ2) = where θ1 and θ2 are acute angles.
Calculate θ1 + θ2 when tan θ1
Sol:
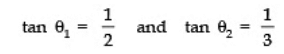
Now, tan (θ1 + θ2) = 1 ⇒ θ1 + θ2 = 45°.
Q2: Prove that:
Sol:
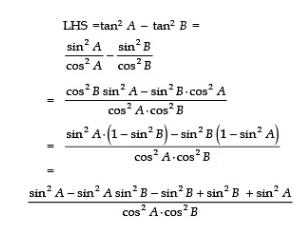
using tanθ=sinθ/cosθ and cos2θ=1-sin2θ as sin2θ+cos2θ=1
Q3: Prove that: (sin4 θ – cos4 θ +1) cosec2 θ = 2
Sol: L.H.S.
= (sin4 θ – cos4 θ + 1) cosec2 θ
= [(sin2 θ)2 – (cos2 θ)2 + 1] cosec2 θ as [a2-b2=(a-b)(a+b)]
= [(sin2 θ – cos2 θ) (sin2 θ + cos2 θ) + 1] cosec2 θ as [ sin2 θ + cos2 θ = 1]
= [(sin2 θ – cos2 θ) *1 + 1] cosec2 θ
= [sin2 θ – cos2 θ+1] cosec2 θ
= [(sin2 θ + (1 –cos2 θ)] cosec2 θ [ 1 – cos2 θ = sin2 θ]
= [sin2 θ + sin2 θ] cosec2 θ
= 2 sin2 θ . cosec2 θ
= 2 = RHS [∵ sin θ . cosec θ = 1]
Q4: Prove that: sec2 θ + cosec2 θ = sec2 θ · cosec2 θ
Sol: L.H.S. = sec2 θ + cosec2 θ
Q5: 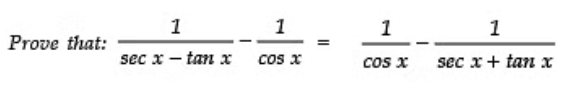
Sol:
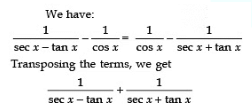
Q6: Given that α + β = 90°, show that:
Sol: ∵ α + β =90°
∵ β = (90 – a)
Q7:
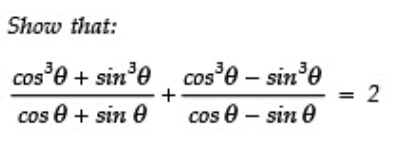
Sol: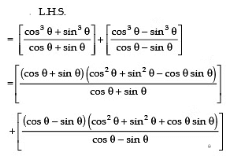
using a3+b3=(a+b)(a2+b2-ab) and a3-b3=(a-b)(a2+b2+ab) in numerator of these terms
and also sin2θ +cos2θ =1
Q8:
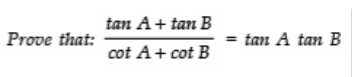
Sol:

using tanθ=sinθ/cosθ and then taking LCM
Q9:
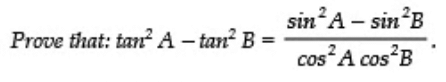
Sol:
Q10: Prove that: sin6θ + cos6θ + 3sin2θ cos2θ = 1.
Sol: ∵ sin2 θ + cos2θ = 1
∵ (sin2 θ + cos2 θ)3 = (1)3 = 1
⇒ (sin2 θ) 3 + (cos2 θ)3 + 3 sin2 θ . cos2 θ (sin2 θ + cos2 θ) = 1
⇒ sin6 θ + cos6 θ + 3 sin2 θ . cos2θ (1) = 1
⇒ sin6 θ + cos6 θ + 3 sin2 θ . cos2 θ = 1
Q11: Prove that: a2 + b2 = x2 + y2 when a cos θ − b sin θ = x and a sin θ + b cos θ =y.
Sol: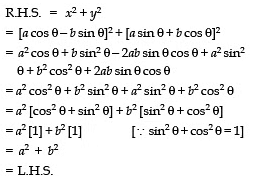
Q12:
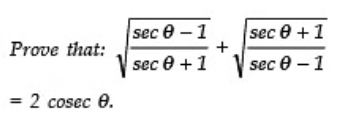
Sol:
Q13:
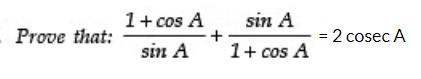
Sol: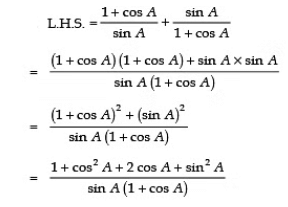
Q14:
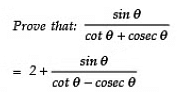
Sol: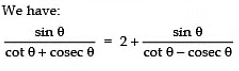
Q15:
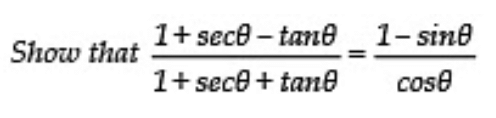
Sol: 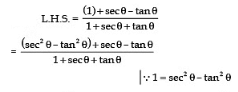
Q16: For an acute angle θ, show that: (sin θ − cosec θ) (cos θ − sec θ)
Sol:
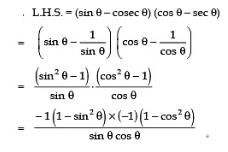
Q17:
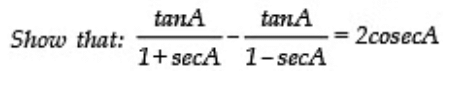
Sol: 
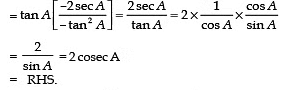
Q18: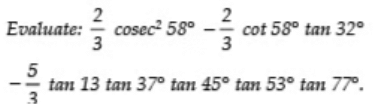
Sol:

Q19:
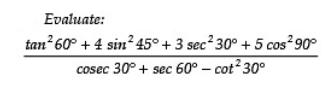
Sol:
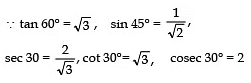
Q20: Without using trigonometric tables evaluate:
Sol:
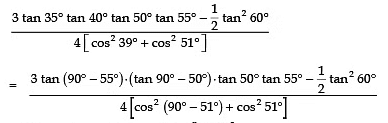
Q21: If tan (A + B) = √3 and tan (A − B) = 1, 0° < A + B < 90°; A > B, then find A and B.
Sol: We have: tan (A + B) = √3 (Given)
tan 60° = √3 (From the table)
⇒ A + B = 60° ...(1)
Also,tan (A − B)= 1 [Given]
and cosec 60° = 2 and cos 90° = 0
⇒ A − B = 45 ...(2)
Adding (1) and (2),
2A = 60° + 45° = 105°
⇒
From (2), 52.5° − B = 45°
⇒ B = 52.5° − 45° = 7.5°
Thus, A = 52.5° and B = 7.5°.
Q22: If tan (2A) = cot (A − 21°), where 2A is an acute angle, then find the value of A.
Sol: We have: tan (2A) = cot (A − 21°)
∵ cot (90°− θ) = tan θ
∴ cot (90°− 2A) = tan 2A
⇒ cot (90°− 2A) = cot (A − 21)°
⇒ 90 − 2A = A − 21°
⇒ − 2A − A = − 21°− 90°
⇒ − 3A = − 111°
⇒
Q23: If sin 3A = cos (A − 10°), then find the value of A, where 3A is an acute angle.
Sol: We have:
sin 3A = cos (A − 10°)
∵ cos (90° − θ) = sin θ
∴ cos (90° − 3A) = sin 3A
⇒ 90° − 3A = A − 10°
⇒ −3A − A = −10° − 90°
⇒ −4A = −100°
⇒
Q24: If sec 2A = cosec (A − 27°), then find the value of A, where 2A is an acute angle.
Sol: We have:
sec 2A = cosec (A − 27°) ...(1)
∵ sec θ = cosec (90° − θ)
∴ sec 2A = cosec (90° − 2A) ...(2)
From (1) and (2), we get
A − 27° = 90° − 2A
⇒ A + 2A = 90 + 27° = 117°
⇒ 3A = 117°
⇒
Q25: Simplify:
+ sin θ cos θ
Sol: We have:
Q26:
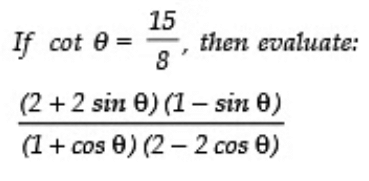
Sol:
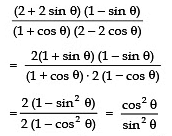
Q27:

Sol:
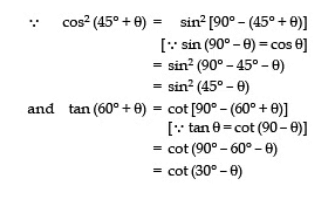
= 1 = R.H.S.
Q28: Without using trigonometrical tables, evaluate:
Sol:
[∵ sin (90° − θ) = cos θ, cos (90° − θ) = sin θ, cosec (90° − θ) = sec θ, and tan (90° − θ) = cot θ]
Q29: Using Geometry, find the value of sin 60°.
Sol: Let us consider an equilateral ΔABC and draw AD ⊥ BC.
Since, each angle of an equilateral triangle = 60°
∴∠A = ∠B = ∠C = 60°
Let AB = BC = AC = 2a
In ΔABD and ΔACD, we have:
AB = AC [Given]
∠ADB = ∠ADC = 90° [Construction]
AD = AD [Construction]
⇒ ΔABD ≅ ΔACD
⇒ BD = CD
Now, using Pythagoras theorem, in right ΔABD,
AD2 = AB2 − BD2
= (2a)2 − a2
= 4a2 − a2
= 3a2
⇒
∴
Thus,
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Maths Chapter 8 Question Answers - Introduction to Trigonometry
| 1. What is the basic definition of trigonometry? |  |
| 2. What are the primary trigonometric ratios? |  |
| 3. How can trigonometry be applied in real life? |  |
| 4. What is the Pythagorean theorem and how does it relate to trigonometry? |  |
| 5. What is the unit circle and why is it important in trigonometry? |  |






















