Class 10 Maths Chapter 8 HOTS Questions - Introduction to Trigonometry

HOTS

Q1: What is the maximum value of   3cosec θ ?

Ans: ∵ 3cosec θ  = 3 sin θ
Since the maximum value of ‘sin θ’ is 1
∴  the maximum value of 3 sin θ is 3 × 1 i.e. 3

⇒  the maximum value of  3cosec θ  is 3.

Q2: If sin θ = 1/3,  then find the value of 9 cot²θ + 9.

Ans: 

cot² θ = cosec² θ - 1

cosec²θ = 1sin²θ   =  1(1/3)²  = 9 

cot² θ = 9 - 1 = 8 

9 cot² θ + 9 = 9(8) + 9 = 72 + 9 = 81 

Thus, the value is 81.

Q3: If 4 tan θ = 3, then find the value of   4 sin θ - cos θ4sin θ + cos θ

Ans: Given $4\; \backslash tan\; \backslash theta\; =\; 3$4 tanθ=3, we have:  tan θ = 34

Let sinθ=3k and cosθ=4k (since $\backslash tan\; \backslash theta\; =\; \backslash frac\{\backslash sin\; \backslash theta\}\{\backslash cos\; \backslash theta\}$tanθ = sinθ/cosθ). Using the identity sin²θ + cos²θ=1:

(3k)² + (4k)² = $19k^2\; +\; 16k^2\; =\; 1$

9k² + 16k² = 1 

25k² = 1

⇒k= 1/5

So, sinθ = 3/5 and $\backslash cos\; \backslash theta\; =\; \backslash frac\{4\}\{5\}$cosθ = 4/5. Now calculate the expression: 

= 4 sin θ - cos θ4sin θ + cos θ

= 4 x 3/5  -  4/5  4 x 3/5 + 4/5  

=   12/5  -  4/5  12/5 + 4/5   

=    8/5   16/5   

= 1/2$\backslash tan\; \backslash theta\; =\; \backslash frac\{3\}\{$

Q4: If sin α = 1/2 and cos β = 1/2 then find the value of (α + β).

Ans: sin 30º = 1/2 , sin α = 1/2  ⇒ α = 30º

cos 60º = 1/2 , cos  β = 1/2  ⇒ β = 60º

⇒ ( α + β) = 30º +  60º = 90º

Q5: If sin θ + cos θ = √3 , find the value of tan θ + cot θ .

Ans: sin θ + cos θ = √3 ⇒ (sin θ + cos θ)² = 3
⇒ sin² θ + cos² θ + 2 sin θ . cos θ = 3
⇒ 1 + 2 sin θ . cos θ = 3 ⇒ 2 sin θ . cos θ = 2 [∴ sin²θ + cos²θ = 1]

⇒ sin θ . cos θ =1 ⇒  1 =  1sin θ .cosθ   

⇒ 1 =   sin²θ + cos²θ  sin θ .cosθ

= sin θ  cosθ + cos θ  sin θ = tanθ + cotθ 

Thus, tanθ + cotθ = 1

Q6: cos (A+B) = 1/2 and sin (A–B) = 1/2 ; 0° < (A + B) < 90° and (A – B) > 0°. What are the values of ∠A and ∠B?

Ans: We have

cos (A+B) = 1/2 ,

Also, cos 60° = 1/2  ⇒ A+B = 60°  ...(1)

Also, sin (A–B) = 1/2 

and  sin 30° = 1/2 ⇒ A - B = 30°     ...(2)

Adding (1) and (2), 2A = 90 ⇒ A = 45
From (1) 45° + B = 60°  ⇒   B = 60° – 45° = 15°
Thus, ∠A = 45° and ∠B = 15°

Q7: Prove that sec²A + cosec²A = sec²A. cosec² A
Ans:  We start with the LHS:

sec²A + cosec²A = 1  cos²A  +  1  sin²A  

Taking a common denominator: 

 sin²A + cos²A  sin² A. cos²A =  1  sin² A. cos²A  

= sec²A⋅cosec²A

Thus, the equation is proved.

$\backslash sec^2\; A\; +\; \backslash csc^2\; A\; =\; \backslash frac\{1\}\{\backslash cos^2\; A\}\; +\; \backslash frac\{1\}\{\backslash sin^2\; A\}$
Q8: Prove that (sinθ + cosecθ)² + (cosθ + secθ)² = tan²θ + cot²θ + 7
Ans:
LHS = sin²θ + cosec²θ + 2sinθcosecθ + cos²θ + sec²θ + 2cosθsecθ
1 + 1 + cot²θ + 1 + tan²θ + 2 + 2
= 7 + tan²θ+cot²θ

Q9: If cos(40^o + x) = sin 30^o, find the value of x, provided 40^o + x is an acute angle.
Ans: Given that
cos(40^o + x) = sin 30^o
Now RHS = sin 30^o = 1/2
So, cos (40^o + x) = 1/2
We know that cos60^o  = 1/2, therefore
40 + x = 60^o
x = 20^o

Q10: Prove that .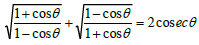
Ans:
LHS =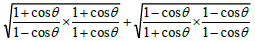
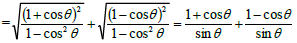(using 1- cos² θ  = sin²θ )

= 1  + cosθ + 1 - cosθsin θ  =  2 sin θ  = 2 cosec θ 

Value-based Questions

(i) Find the length of the ladder.
 (ii) Which mathematical concept is used in this problem?
 (iii) By putting up a banner in favour of respect to women, which value is depicted by the group of students?

Ans: (i) Let AB be the ladder and CA be the wall with the window at A. Also,
BC = 2.5 m
CA = 6m
∴ In rt ΔACB, we have
AB² = BC² + CA² [Using Pythagoras Theorem]
= (2.5)² + (6)²
= 6.25 + 36 = 42.25

⇒   AB = √42.25 =6.5 m 

Thus, the length of the ladder is 6.5 m.
(ii) Triangles (Pythagoras Theorem)
(iii) Creating positive awareness in public regarding women.

Q2: Raj is an electrician in a village. One day power was not there in entire village and villagers called Raj to repair the fault. After thorough inspection he found an electric fault in one of the electric pole of height 5 m and he has to repair it. He needs to reach a point 1.3m below the top of the pole to undertake the repair work. On the basis of above, answer the following question.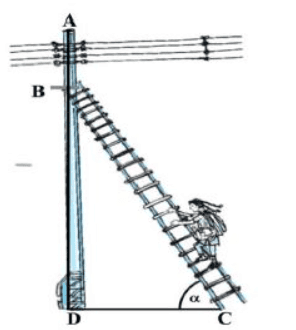

(i) When the ladder is inclined at an angle of α such that 3tan α + 2 = 5 to the horizontal, find the angle $\backslash al$α.
(ii) How far from the foot of the pole should he place the foot of the ladder? (Use $\backslash sqrt\{3\}\; =\; 1.73$3=1.73)
(iii) In the above situation, find the value of sin α cos α2 - cos α sin α2
(iv) In the above situation, if BD=3 cm and BC=6 cm, find α.
(v) In your opinion, how does Raj's action reflect the values of responsibility and community service?

Ans: 
(i) Given the equation 3tanα+2=5, simplify to find $\backslash tan\; \backslash alpha$tanα:

√3 tan α = 5 - 2 = 3 

tan α = 3√3  = √3 

We know that tan60º=3, so the angle α=60º. 

(ii) Raj needs to reach a height of 3.7m (since $5-1.3=3.7\hspace{0.17em}m5\; -\; 1.3\; =\; 3.7\; \backslash ,\; \backslash text\{m\}$) and the ladder is inclined at 60º. 

Using tan60º = 3.7/x and knowing tan60º = 1.73, we get: 

x =  3.71.73  = 2.14 m 

$\backslash cos\; 60^\backslash circ\; =\; \backslash frac\{\backslash text\{adjacent\}\}\{\backslash text\{hypotenuse\}\}\; =\; \backslash frac\{x\}\{5\}$