Class 10 Maths Chapter 6 Question Answers - Triangles
Q1. In the figure, if ∠BAC = 90° and AD ⊥ BC. Then,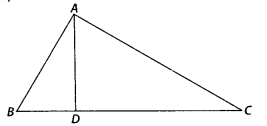
(A) BD . CD = BC2
(B) AB . AC = BC2
(C) BD . CD = AD2
(D) AB . AC = AD2
Solution:
(C)
In ∆ABC,
∠B + ∠BAC + ∠C = 180°
⇒ ∠B + 90° + ∠C = 180°
⇒ ∠B = 90° – ∠C
Similarly, In ∆ADC, ∠D AC = 90° – ∠C
In ∆ADB and ∆ADC,
∠D = ∠D = 90°
∠DBA = ∠D AC [each equal to (90° – ∠C)
∴ ∆ADB ~ ∆CDA
[by AA similarity criterion]
∴ BDAD=ADCD
⇒ BD . CD = AD2
Q2. If ∆ABC ~ ∆EDFand ∆ABC is not similar to ∆DEF, then which of the following is not true?
(A) BC . EF = AC . FD
(B) AB . EF = AC . DE
(C) BC . DE = AB . EF
(D) BC . DE = AB . FD
Solution:
(C)
Given, ∆ABC ~ ∆EDF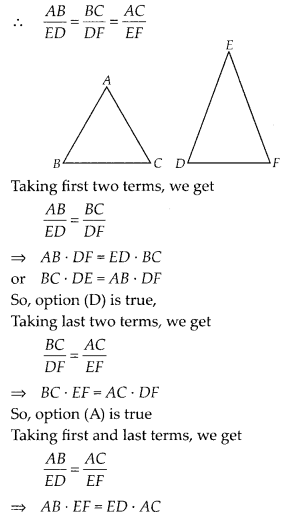
Hence, option (B) is true.
Q3. A peacock is sitting on the top of a pillar, which is 9 m high. From a point 27 m away from the bottom of the pillar, a snake is coming to its hole at the base of the pillar. Seeing the snake, the peacock pounces on it. If their speeds are equal, at what distance from the hole is the snake caught?
Sol. Let the position of hole is at ‘H’ and snake be at ‘S’. If the point ‘P’ represents the peacock and let the distance between hole to the place where they meet = x metres
∴ SH = 27 m = PC
[Πtheir speeds are equal]
Now SC = (27 - x) m
PC = (27 - x) m
In right D PHC, we have:
PH2 + CH2 = PC2
[By Pythagoras Theorem]
⇒ (9)2 + (x)2 = (27 - x)2
⇒ 81 + x2 = 729 - 54x + x2
⇒ 54x = 729 - 81 = 648
⇒ x = 648/54=12m
Hence, the required distance = 12 m.
Q4. Prove that in a right triangle the square on the hypotenuse is equal to the sum of the squares of the other two sides.
Making use of the above, prove the following:
In a rhombus ABCD, prove that:
4 AB2 = AC2 + BD2
Sol. Part-I . [see proof of Pythagoras Theorem]
Part-II.
We have a rhombus ABCD whose diagonals AC and BD intersect at O.
Since the diagonals of a rhombus bisect each other at right angles.
∴ AC ≌ BD And
OA = OC
OB = OD
In right Δ AOB, we have
AB2 = OA2 + OB2
[using the above result]
AB2 = AC2 2 + BD2 2
⇒ AB2 = AC24 + BD24 = AC2 + BD24
⇒ 4AB2 = AC2 + BD2
Q5. Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Using the above, do the following:
If D is a point on the side AC of D ABC such that AD: DC = 2 : 3 and E is a point on BC such that DE y AB; then find the ratio of areas of Δ ABC and Δ CDE.
Sol. Part-I [See the proof of the theorem]
Part-II. We have D ABC in which
DE y AB
∴ In Δ ABC and Δ DEC,
<C = <C [Common]
<1 = <2 [Corresponding
Using AA similarity,
Δ ABC ~ Δ DEC
⇒ ar(△DEC)ar(△ABC) = (CD)(CA) 2 ...(1)
Since, AD : DC = 2 : 3 [Given]
Let AD = 2x, DC = 3x
∴ AC = AD + DC = 2x + 3x = 5x
∴ CDCA = 3x5x = 35 ...(2)
From (1) and (2), we get
ar(△DEC)ar(△ABC) = (3)(5) 2 = 925
⇒ ar(△ABC) : ar(△DEC) = 25 : 9
Q6. Prove that, in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Using the above, do the following:
Prove that, in a D ABC, if AD is perpendicular to BC, then
AB2 + CD2 = AC2 + BD2
Sol. Part-I See the proof of the Pythagoras Theorem]
Part-II We have Δ ABC in which AD ⊥ BC
∴ In right D ADB, <D = 90°
∴ Using Pythagoras theorem,
AB2 = AD2 + BD2
⇒AD2 = AB2 - BD2 ...(1)
Similarly, in right D ADC
AC2 = AD2 + CD2
⇒ AD2 = AC2 - CD2 ...(2)
From (1) and (2), we get
AB2 - BD2 = AC2 - CD2
AB2 + CD2 = AC2 + BD2
Q7. ABCD is a trapezium with AB y DC. E and F are points on non-parallel sides AD and BC respectively such that EF is parallel to AB. Show that = AEED = BFFC
Sol. Join AC such that it meets EF at G.
ABy DC and EFy AB
∴ EF y DC [Q Lines parallel to the same line are parallel to each other]
In Δ ADC
EG y DC [Q EG is a part of EF]
⇒ AEED = AGGC ...(1)
Next in DCAB
= AGGC = BFFC ...(2)
From (1) and (2), we get
AEED = BFFC
Q8. ABCD is a trapezium in which AByDC and P and Q are points on AD and BC, respectively such that PQy DC. If PD = 18 cm, BQ = 35 cm and QC = 15 cm, find AD.
[NCERT Exemplar]
Sol. Since AByDC and PQyDC
⇒ APPD = BQCQ ...(1)
Substituting
PD = 18 cm, BQ = 35 cm
and CQ = 15 cm in (1), we get
=
AP18 = 3515
⇒ AP = 18 × 3515 cm
= 6 × 7 cm = 42 cm
AD = AP + PD
AD = 42 cm + 18 cm = 60 cm
Since, AD = AP + PD
∴ AD = 42 cm + 18 cm = 60 cm
Q9. The hypotenuse of a right triangle is 25 cm and out of the remaining sides, one is longer than the other by 5 cm. Find the lengths of the other two sides.
Sol. Hypotenuse of the rt triangle = 25 cm
Let one of the sides be x cm
∴ Other side = (x + 5)cm
Now, using Pythagoras Theorem,
x2 + (x + 5)2 = 252
⇒ x2 + x2 + 10x + 25 = 625
⇒ 2x2 + 10x = 625 – 25 = 600
or x2 + 5x – 300 = 0
or x2 + 20x – 15x – 300 = 0
or x(x + 20) – 15 (x + 20)
or (x – 15) (x + 20) = 0
Either x – 15 = 0
⇒ x = 15
or x + 20 = 0
⇒ x = – 20
x = – 20
is not required.
Therefore, x = 15
Now, x + 5 = 15 + 5 = 20
The other two sides are 15 cm and 20 cm.
|
127 videos|674 docs|84 tests
|
FAQs on Class 10 Maths Chapter 6 Question Answers - Triangles
| 1. What are the different types of triangles? |  |
| 2. How do you calculate the area of a triangle? |  |
| 3. What is the Pythagorean theorem and how is it used in triangles? |  |
| 4. How can we determine if three given side lengths form a triangle? |  |
| 5. How can we prove that two triangles are congruent? |  |

















